Salut
Ici je n arrive pas trouver lesquels des ces vecteurs sont colinéaires ?
Je sais pas si on peut reprendre un vecteur qui a déjà été mis en couple.
Les voici et mes données:

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
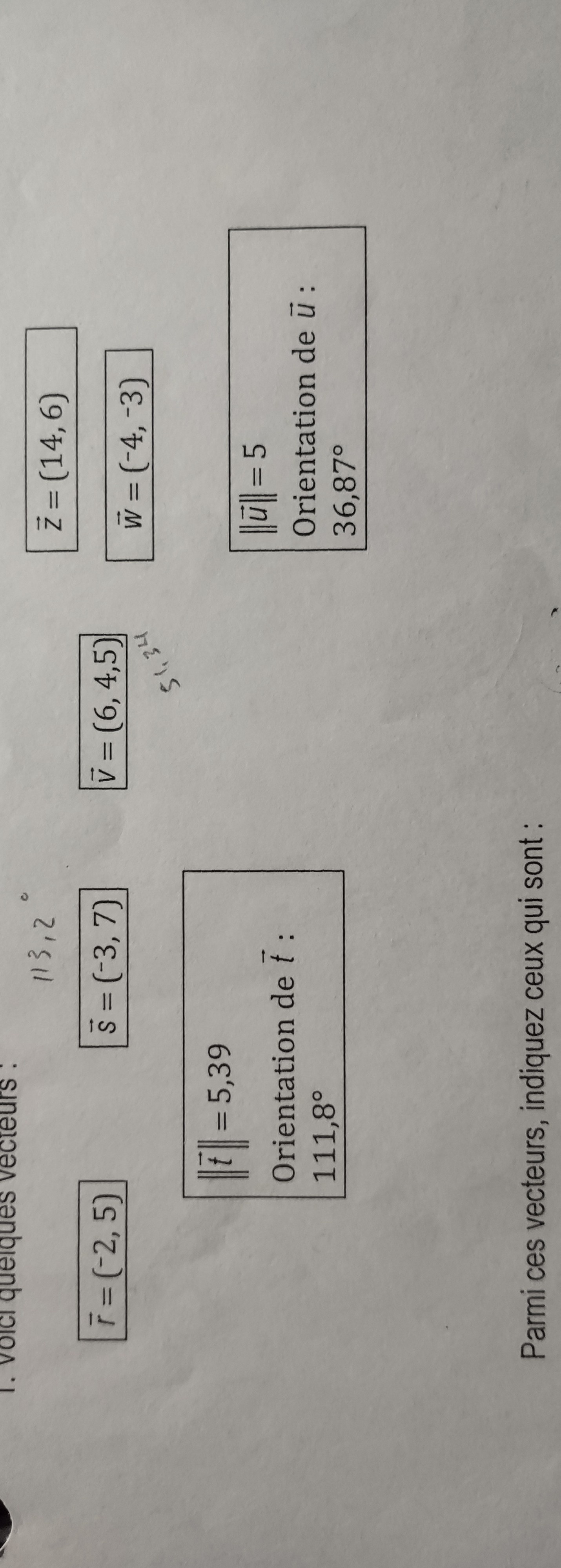
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Merci pour l aide !








Explication d'Alloprof
Cette explication a été donnée par un membre de l'équipe d'Alloprof.
Salut 😁
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Tu dois alors voir si tu peux multiplier un vecteur par un nombre réel, et que ça donne l'autre.
Reprenons les différents vecteurs (je ne peux pas faire la miniflèche en haut des lettres des vecteurs, mais imagine qu'elle est là 😊) :
r = (-2, 5)
s = (-3, 7)
v = (6, 4,5)
z = (14, 6)
w = (-4, -3)
Pour trouver les composantes des deux autres, voici comment procéder :
t = tu trouves la composante x avec sin de l'angle, et la composante y avec cos de l'angle.
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
u = tu trouves la composante x avec cos de l'angle, et la composante y avec sin de l'angle.
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Tu as donc les bons vecteurs t = (-2,5) et u = (4, 3).
Les vecteurs r et t sont donc colinéaires et équipollents à la fois, ils répondent aux deux définitions.
Pour finir, en vérifiant si les différents vecteurs sont des multiples les uns des autres, il faut le faire pour chaque paire, on obtient aussi w et u qui sont colinéaires, le nombre réel qui les multiplie est -1.
Dis-nous si tu as d'autres questions 😎 À bientôt sur la Zone 😊
Suggestions en lien avec la question
Suggestion en lien avec la question
Voici ce qui a été trouvé automatiquement sur le site, en espérant que ça t’aide!