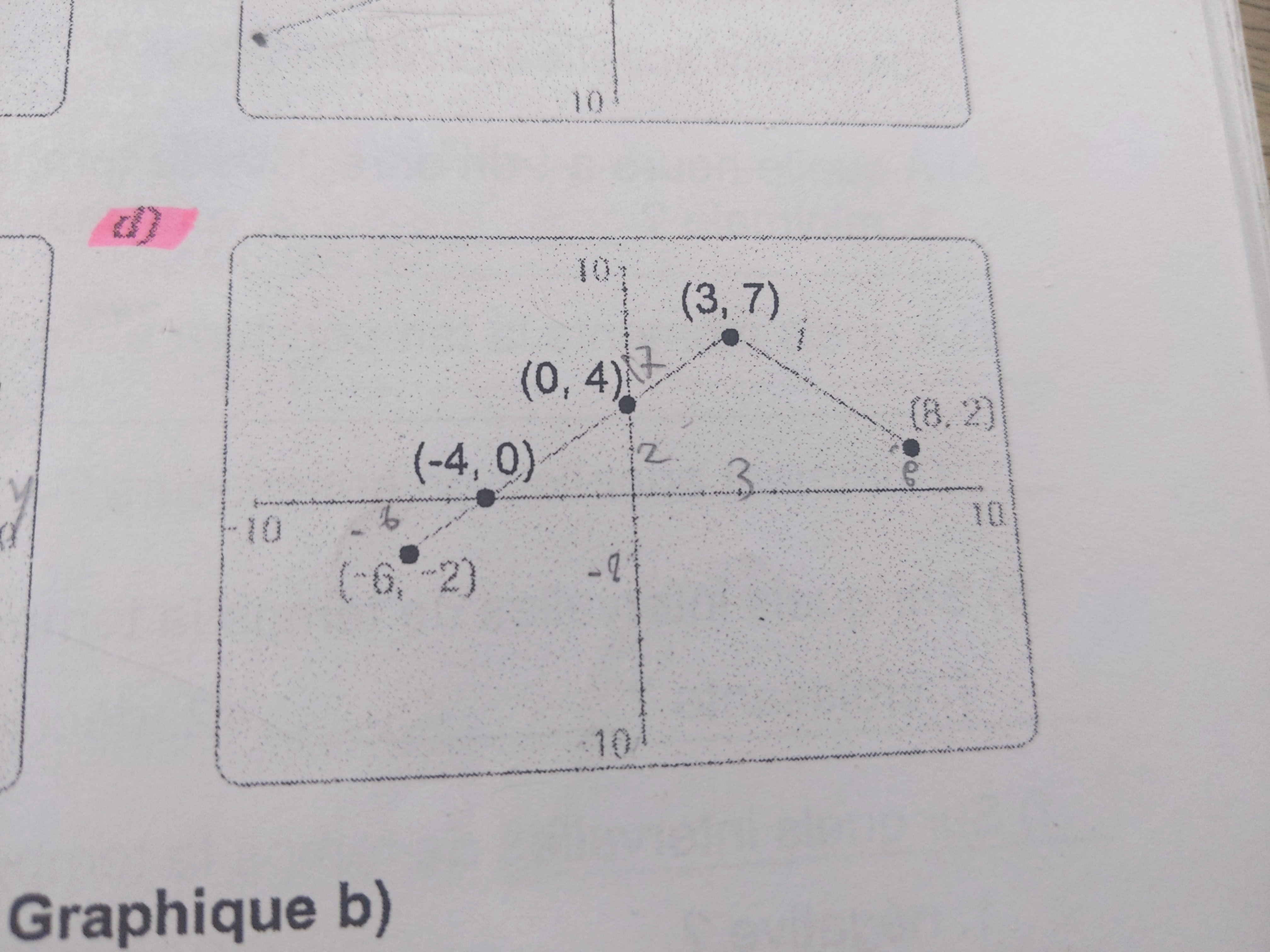
Dans le graphique de est-ce que c'est -6,8 et pour l'image -2,7 ?

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
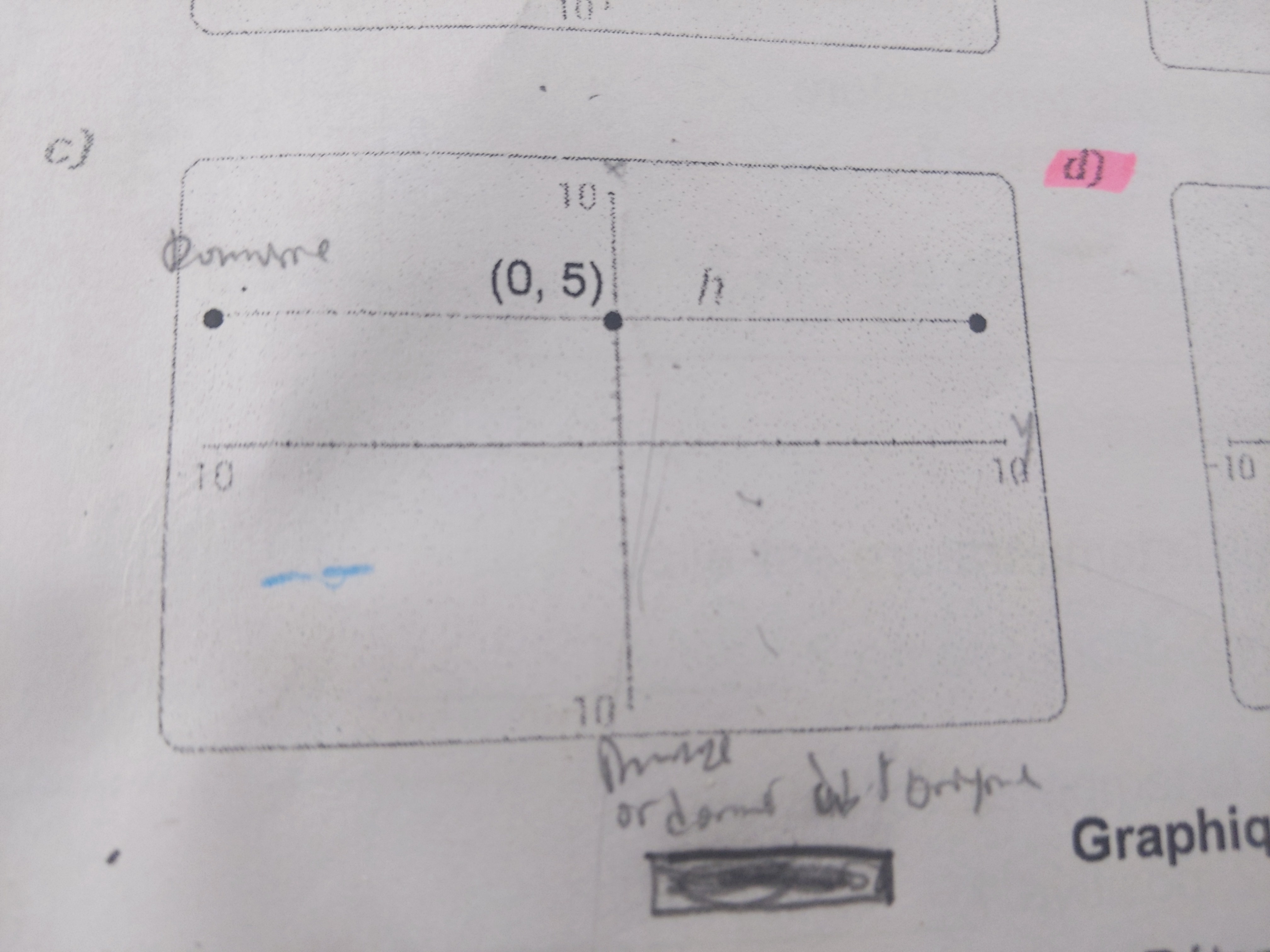
Il y a plusieurs point pour le domaine et l'image pouvez-vous m'expliquer lorsque il y a des points dans la zone. Ou si par exemple il n'y a pas de points comme ici. L'image commence par où merci
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.









Explication d'Alloprof
Cette explication a été donnée par un membre de l'équipe d'Alloprof.
Salut!
En réalité, sur ce graphique, il y a une infinité de points qui composent la fonction i(x), il n'y a pas que les 5 points dessinés!
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Le fait que ces points soient illustrés ou non n'a donc aucune importance!
Le domaine d'une fonction représente les valeurs possibles en x. Ainsi, pour trouver le domaine, tu dois seulement repérer le point le plus à droite et celui le plus à gauche, et vérifier que la fonction existe dans cet intervalle-là (c'est-à-dire vérifier que la fonction ne s'arrête pas en plein milieu, qu'il n'y a pas de valeur en x entre les deux bornes identifiés pour laquelle la fonction n'existe pas, qu'il n'y a pas de point ouvert).
Ainsi, le domaine de la fonction i(x) est bien [-6, 8], puisque la fonction existe de x=-6 à x=8. Son image est de [-2, 7], car la fonction existe de y=-2 à y=7.
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Le domaine de la fonction h(x) est [-10, 10], car la fonction existe de x=-10 à x=10. Son image est {5}, car la fonction existe uniquement à y=5.
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Voici un autre exemple qui pourrait t'aider à mieux comprendre cette notion. Nous avons cette fonction définie par parties :
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Son domaine est ]-∞, -1[ U ]2, 6].
En effet, dans la première portion de la fonction (la droite décroissante à gauche), la droite dépasse le graphique, on peut donc conclure qu'elle continue jusqu'à l'infini négatif. Chaque fois que l'on a un infini dans un intervalle, il faut exclure la borne (]-∞ et non [-∞). Puis, cette droite continue jusqu'à x=-1. Or, à x=-1, on a un point ouvert, ce qui signifie que la fonction n'existe pas à x=-1 précisément. Il faut donc exclure la borne dans l'intervalle du domaine, d'où ]-∞, -1[.
Ensuite, la fonction reprend à x=2 avec une seconde droite. Le domaine de cette droite est ]2, 6], car elle existe de x=2 EXCLUSIVEMENT (point ouvert) à x=6 INCLUSIVEMENT (point fermé).
Le domaine final de cette fonction est l'union des domaines de chacune des droites, d'où ]-∞, -1[ U ]2, 6].
Voici la vidéo d'où est tiré cet exemple : 8.2.2 Domaine et Ensemble Image d'une fonction - YouTube
J'espère que c'est plus clair pour toi! :)
Suggestions en lien avec la question
Suggestion en lien avec la question
Voici ce qui a été trouvé automatiquement sur le site, en espérant que ça t’aide!