Secondaire 4 • 1a
Re-bonjour!
Merci à madame Katia de m'avoir transmis une explication. J'avais en effet oublié d'insérer une partie de mon numéro. Je vous l'affiche ci-dessous au complet :)
Comme vous l'avez suggéré, j'ai essayé d'avoir une seule équation qui ne comporte qu'une seule variable, soit le x2. Mais, le problème c'est qu'une fois que je dois isoler x2, je ne peux pas parce que ils vont s'annuler tout de même en raison de la fraction.
Je me sens vraiment stupide. S.v.p aidez-moi, j'ai un blocage horaire cette semaine :C
Voici la partie que j'ai essayé en suivant votre explication:
Merci !!!

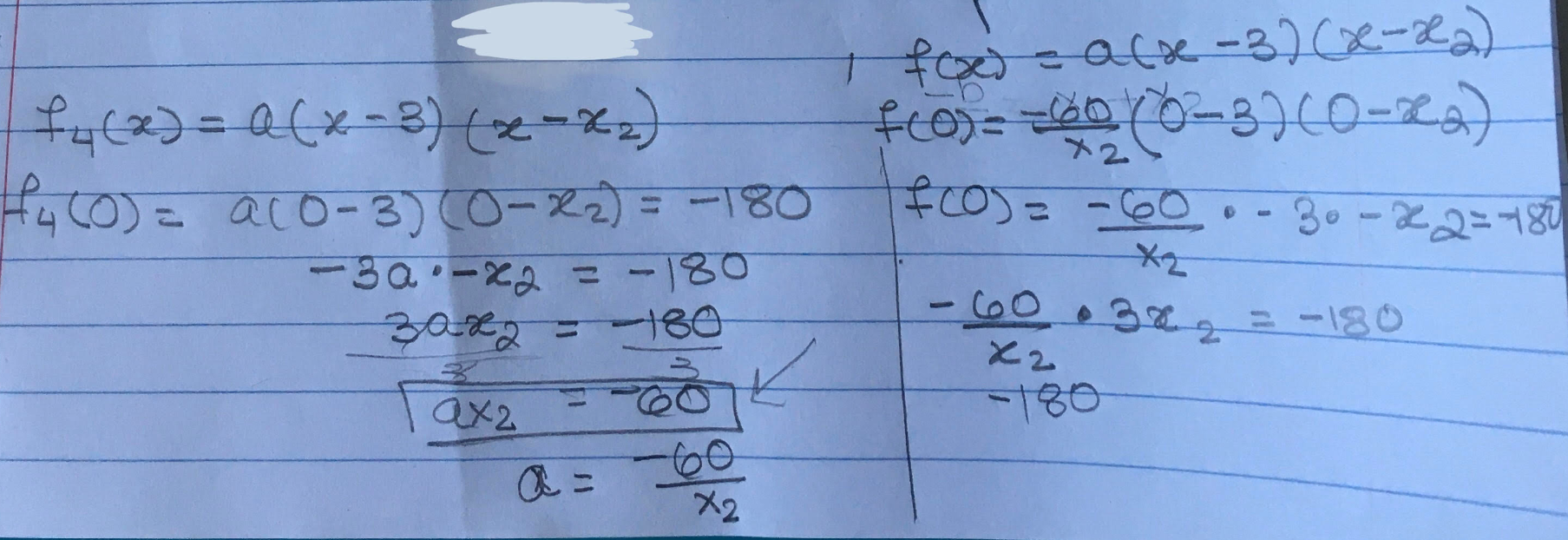






Explication d'Alloprof
Cette explication a été donnée par un membre de l'équipe d'Alloprof.
Salut!
Il ne faut pas du tout que tu te sentes stupide, tu as fait une petite erreur que beaucoup font, examinons le tout ensemble pour y voir plus clair :)
C'est tout à fait normal que les \(x_{2}\) s'annulent, puisque tu réutilises la même équation! ;)
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Il faut se rappeler qu'on doit toujours avoir autant d'inconnus que d'équations. Puisqu'on a 2 inconnus, soit \(a\) et \(x_{2}\), alors on a besoin de deux équations différentes pour pouvoir trouver la valeur de ces inconnus. Si on n'a qu'une seule équation, alors il est impossible de trouver la valeur des deux variables, on peut seulement exprimer une des variables en fonction de l'autre et ainsi n'avoir qu'un seul inconnu dans l'équation, comme tu as fait ici :
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Ainsi, tu ne peux pas réutiliser la même équation, tu n'obtiendras pas de résultat!
On sait que la somme des zéros est particulière :
\(x_{1}\)+\(x_{2}\)= somme particulière
3+\(x_{2}\)= somme particulière
et on sait aussi que \(x_{2}\) est un nombre entier.
Tu peux analyser les trois autres sommes obtenues :
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
et déterminer une somme possible pour les zéros de f4. Puis, tu pourras calculer \(x_{2}\) en fonction de cette somme, déterminer la règle de f4 et finalement trouver son image.
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Je te laisse essayer avec ces indices. Reviens nous voir si tu as besoin d'aide supplémentaire! :)
D'abord avant de vouloir resoudre pour a, il faut que tu aies la valeur de x2. Pour ce faire il faudrait pour toi que tu fasses une petite observation quant a la somme des zeros. En gros, il faudrait que tu fasses une relation entre la somme et le carre d'un des deux zeros...
Suggestions en lien avec la question
Suggestion en lien avec la question
Voici ce qui a été trouvé automatiquement sur le site, en espérant que ça t’aide!