Secondaire 5 • 2a
Salut,
J'ai trouvé que la restriction était x est plus petit ou égal à-3 et l'équation me donne à un moment donné -32 d'un côté donc je ne comprenais pas pourquoi l'inéquation est impossible. Pouvez-vous m'indiquer (encore une fois) où j'ai fait ma faute svp? Merci et bonne soirée. C'est la d)
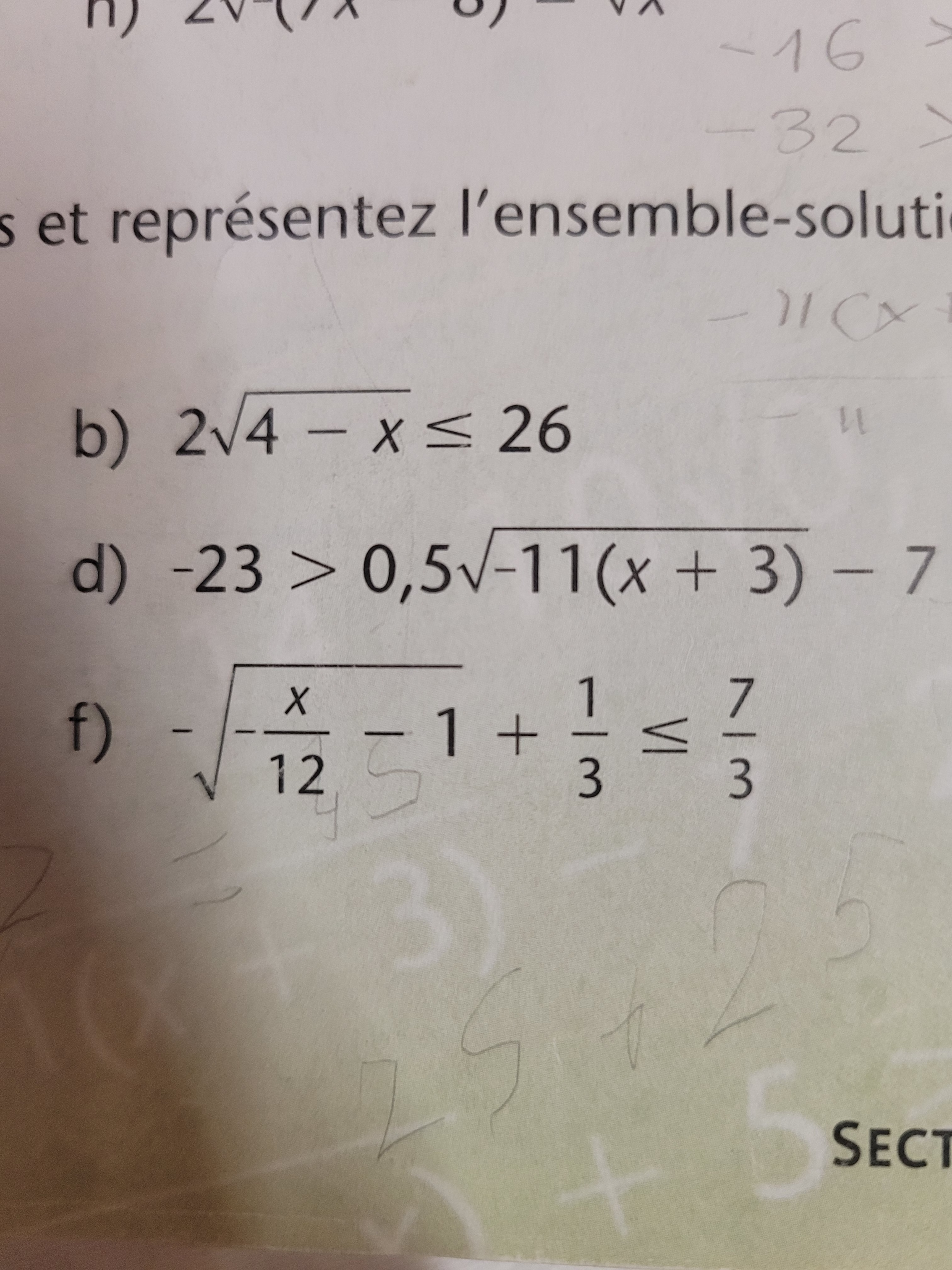






Explication vérifiée par Alloprof
Cette explication a été vérifiée par un membre de l’équipe d’Alloprof.
-23 > 0.5 racine (-11(x+3)) -7
Domaine de définition
-11(x+3) >= 0 comme -11 est négatif pour obtenir un produit positif il faut que (x+3) soit négatif
(négatif * négatif)=positif
(x+3) =< 0 ----- x =< -3
Ton domaine de définition est tous les x =< -3
-23 > 0.5 racine (-11(x+3)) -7
On passe le -7 de l'autre cote en changeant son signe.
-23+7 > 0.5 racine (-11(x+3))
-16 > 0.5 racine (-11(x+3))
Ou une autre facon de l'écrire si A > B ca veut aussi dire que B < A
0.5 racine (-11(x+3)) < -16
on divise par 0.5 et on ne change pas l'inégalité parce que 0.5 est positif.
racine (-11(x+3)) < -16/0.5
racine (-11(x+3)) < -32
Et c'est impossible paracerque la racine carre d'un nombre est toujours positive et ici il y a une contradiction la racine carre est inferieure a un nombre négatif, donc elle est négative, or on sait que la racine carrée est tout le temps positive, contradiction.
Le problème n'as pas de solution.
c'est comme si on te demandes de trouver un nombre qui est inferieur à -32 et supérieur à 0, c'est impossible à trouver.
Suggestions en lien avec la question
Suggestion en lien avec la question
Voici ce qui a été trouvé automatiquement sur le site, en espérant que ça t’aide!