Secondaire 5 • 2a
Est-ce que ce serait possible de savoir ce que donne x en ayant une photo du problème logarithmique résolue à la main car je suis très visuelle et je n’est pas compris les autres explications. (TS5)
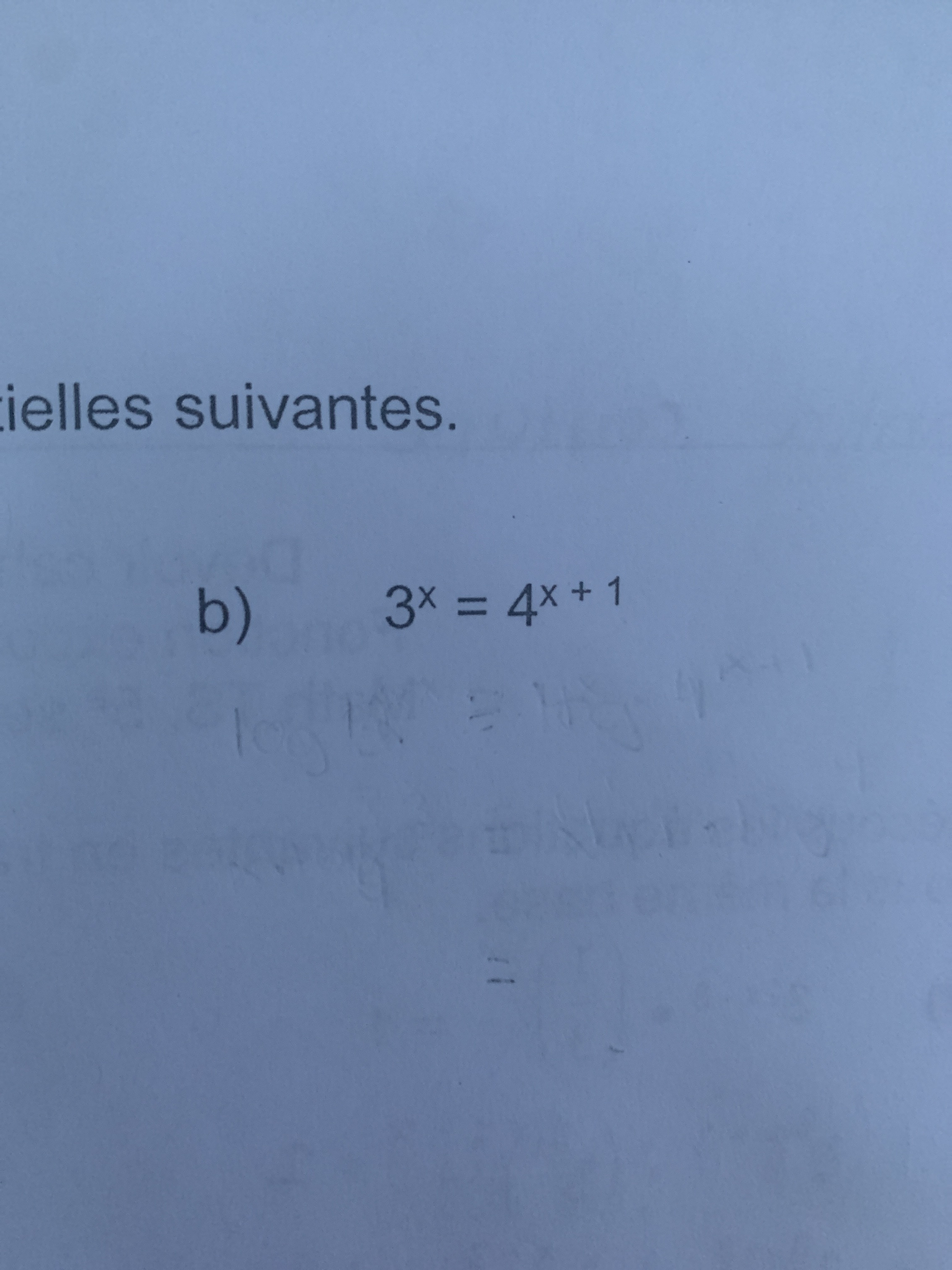






Explication d'Alloprof
Cette explication a été donnée par un membre de l'équipe d'Alloprof.
Bonjour,
Voici la résolution de façon claire :
$$ 3^x = 4^{x+1} $$
$$\log(3^x) = \log(4^{x+1})$$
$$x*\log(3) = (x+1)* \log(4)$$
$$x * \frac{\log(3)}{\log(4)} = x+1$$
$$x * \frac{\log(3)}{\log(4)} - x = 1$$
$$x * 0.792 - x = 1$$
$$x * 0.792 - x = 1$$
$$-0,208 * x = 1 $$
$$ x = \frac {1}{-0,208} = -4.81$$
Bonne journée :)
Suggestions en lien avec la question
Suggestion en lien avec la question
Voici ce qui a été trouvé automatiquement sur le site, en espérant que ça t’aide!