Skip to content

Zone d’entraide

Question de l’élève

English
2
Retour
avatarMelonAdorable6131
Secondaire 4 • 1a
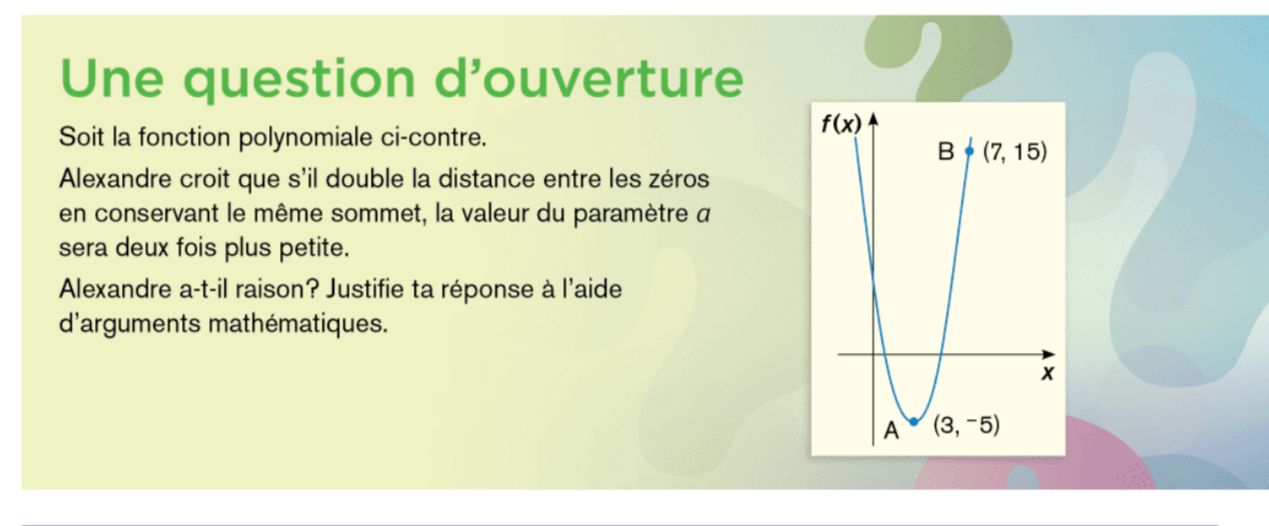
image.png

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

i-icon

J'ai fais cet exercise et j'ai réussi à prouver numériquement (avec des nombres) que lorsqu'on double la distance entre les zéros, le a devient 4 fois plus petit. Par contre, je n'arrive pas à trouver comment je peux prouver ça algébriquement. Merci de m'aider s'il vous plait.

Mathématiques
Donner une explication
avatar
avatar

{t c="richEditor.description.title"} {t c="richEditor.description.paragraphMenu"} {t c="richEditor.description.inlineMenu"} {t c="richEditor.description.embed"}

Soumettre mon explicationSoumettre mon explication

Explications (2)

  • Explication d'un(e) pro de la Zone d'entraide Explication d'un(e) Pro

    Explication d'un(e) pro de la Zone d'entraide

    Tu peux faire confiance à cette explication, car elle est donnée par une personne identifiée comme étant fiable par Alloprof.

    Options
      avatarRenardComique299teacher check
      Pro de la zone d’entraide • 1a

      Salut :D

      Voici ma démarche, mais je te conseille de seulement regarder le début (la 1re image) et essayer de faire le reste par toi-même.

      Si mon écriture ne te semble pas compréhensible (ce qui est très possible), dis-toi que je suis toujours ouverte à apporter plus de clarifications.

      image.png

      Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

      i-icon


      image.png

      Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

      i-icon


      image.png

      Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

      i-icon


      Ne lâche pas

      Bonne journée :)

    • Explication d'Alloprof

      Explication d'Alloprof

      Cette explication a été donnée par un membre de l'équipe d'Alloprof.

      Options
        avatarRamzi Zteacher check
        Équipe Alloprof • 1a

        Salut !

        L'exercice s'effectue en deux étapes. La première est de trouver la règle de la fonction \(f(x)\) à l'aide des informations du graphique.


        https://www.alloprof.qc.ca/fr/eleves/bv/mathematiques/trouver-la-regle-d-une-fonction-polynomiale-de-degre-2-m1247

        $$ f(x)=a(x-h)^2+k $$

        Il est possible de trouver la valeurs des zéros à l'aide de cette règle.

        La deuxième partie consiste à trouver la règle de la deuxième fonction. Le sommet reste le même, mais tu dois trouver la nouvelle valeur des zéros en doublant la distance entre les deux.

        J'espère que cela ait pu t'aider et si tu as d'autres questions, n'hésite pas !

        Bonne journée !

      Québec RioTinto Desjardins Pathy TROTTIER OTHER
      Poser une question