Secondaire 5 • 2a
Salut :D
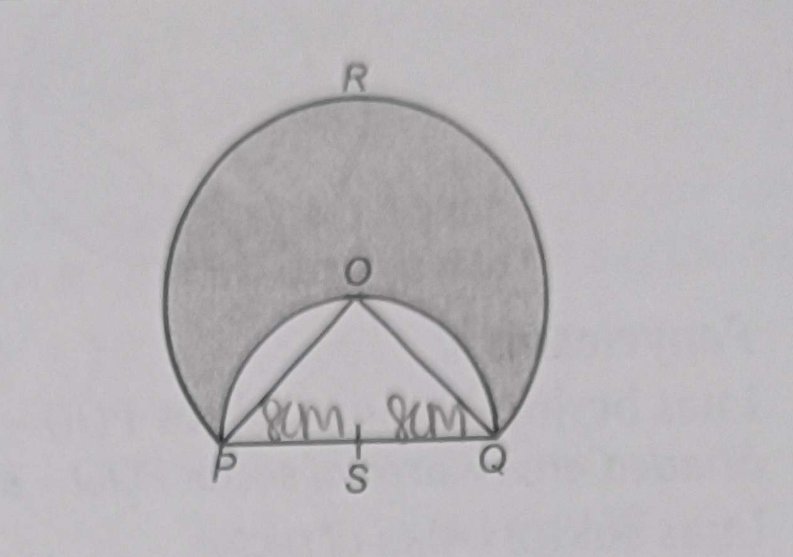
Le diagramme montre un secteur majeur OPRQ de centre O
OQP est un demi-cercle de centre S avec un rayon de 8cm.
Montrez que l'aire de la partie ombrée est égale à 32(π+2).
Avant de lire ma démarche, vous pouvez essayer de résoudre le problème au cas où que ma démarche vous induise en erreur car elle est possiblement erronée.
Pourquoi l'aire de la partie ombrée n'est pas égale à 64(π+1) ?
J'ai calculé l'aire du triangle OQP : 16*8/2 = 64 cm²
- mOS=8 car si on trace un segment OS, les triangles OPS et OQS sont triangles rectangles isocèles
J'ai calculé l'aire des deux parties bombées :
A demi cercle - A triangle = 8²π/2 - 64 = 32π-64 cm²
On obtient la réponse en soustrayant 3/4 de l'aire du secteur majeur par les deux parties bombées :
(8√2)²(π)(3/4) - (32π-64) = 64π + 64 = 64(π+1) cm²
- le rayon du grand secteur est de 8√2 car rayon=mOP= √(8²+8²)
Merci beaucoup ♥






Explication vérifiée par Alloprof
Cette explication a été vérifiée par un membre de l’équipe d’Alloprof.
Oui, c'est une bonne pratique de regarder le problème indépendamment d'abord. Et c'est ce que j'ai fait et j'arrive au même résultat que toi. L'aire ombragée est de 64 (π + 1).
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Suggestions en lien avec la question
Suggestion en lien avec la question
Voici ce qui a été trouvé automatiquement sur le site, en espérant que ça t’aide!