Secondaire 4 • 2a
Bonjour!
Je ne sais pas comment on pourrait trouver le(s) point(s) d'intersection de ce système d'équations (dans l'image) par substitution! Est-ce que vous pourriez me montrer la démarche correcte svp?
Merci!!
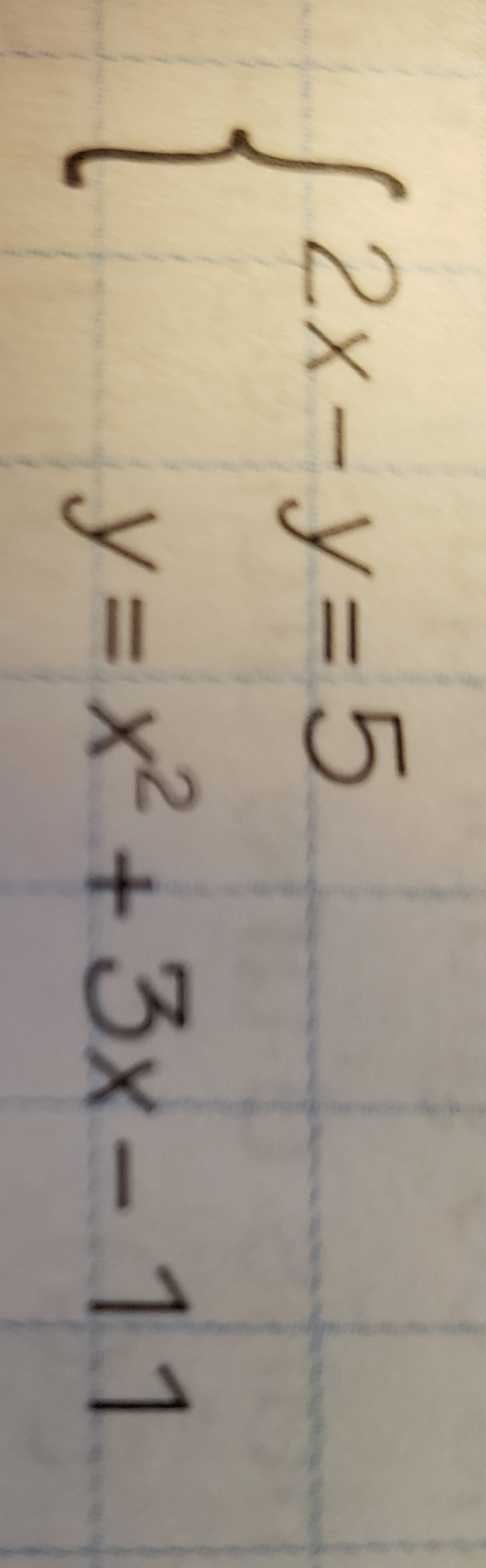






Explication d'Alloprof
Cette explication a été donnée par un membre de l'équipe d'Alloprof.
Salut!
Donc on a :
$$ \left\{ \begin{array}{ll} 2x - y = 5 \\ y = x^2 + 3x - 11 \end{array} \right. $$
On va remplacer y dans la première équation par ce que y vaut dans la seconde équation, comme ceci :
$$ 2x - (x^2 + 3x - 11 ) = 5 $$
Puis, on résout. On commence par distribuer le signe négatif à l'intérieur de la parenthèse :
$$ 2x - x^2 - 3x + 11 = 5 $$
On additionne les termes semblables 2x et -3x :
$$ - x^2 - x+ 11 = 5 $$
On déplace la constante 5 de l'autre côté de l'équation :
$$ - x^2 - x+ 11 -5 = 5-5 $$
$$ - x^2 - x+ 6= 0 $$
On peut ensuite factoriser l'expression avec la méthode du produit-somme, ou encore avec la formule quadratique.
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Utilisons la méthode de la formule quadratique. On a alors :
$$ x_{1,2} = \frac{-(-1)±\sqrt{(-1)^2-4(-1)(6)}}{2(-1)}$$
$$ x_{1,2} = \frac{1±\sqrt{1+24}}{-2}$$
$$ x_{1,2} = \frac{1±\sqrt{25}}{-2}$$
$$ x_{1,2} = \frac{1±5}{-2}$$
On divise notre équation en deux équations et on les résout:
$$ x_{1} = \frac{1+5}{-2}$$
$$ x_{1} = \frac{6}{-2} = -3$$
et
$$ x_{2} = \frac{1-5}{-2}$$
$$ x_{2} = \frac{-4}{-2}=2$$
Voilà! On a donc deux points d'intersection, soit x=-3 et x=2
J'espère que c'est plus clair pour toi! Si tu as d'autres questions, on est là! :)
Explication d'un(e) pro de la Zone d'entraide
Tu peux faire confiance à cette explication, car elle est donnée par une personne identifiée comme étant fiable par Alloprof.
Bonjour ArsenicDelta,
Merci pour ta question :)
Je te dirais d'aller mettre ton y tout seul pour après faire tes opérations inverses avec y1 = y2.
2x - y = 5
( y négatif donc mettre y positif pour le mettre de l'autre côté )
2 x = y + 5
( 5 positif donc, va devenir -5 de l'autre côté )
2x - 5 = y
Avec tes deux règles tu pourras faire ta méthode de y1 = y2 avec les opérations inverses
J'espère t'avoir aidée !
N'hésite pas si tu as d'autres question :D
BrachiosaureTimide314
Suggestions en lien avec la question
Suggestion en lien avec la question
Voici ce qui a été trouvé automatiquement sur le site, en espérant que ça t’aide!