Bonjour, je dois trouver le point d’intersection entre 2 fonctions mais je n’y arrive pas. Que j’utilise la méthode algébrique ou la table de valeurs, y1 et y2 n’ont jamais de x similaire. Merci!
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
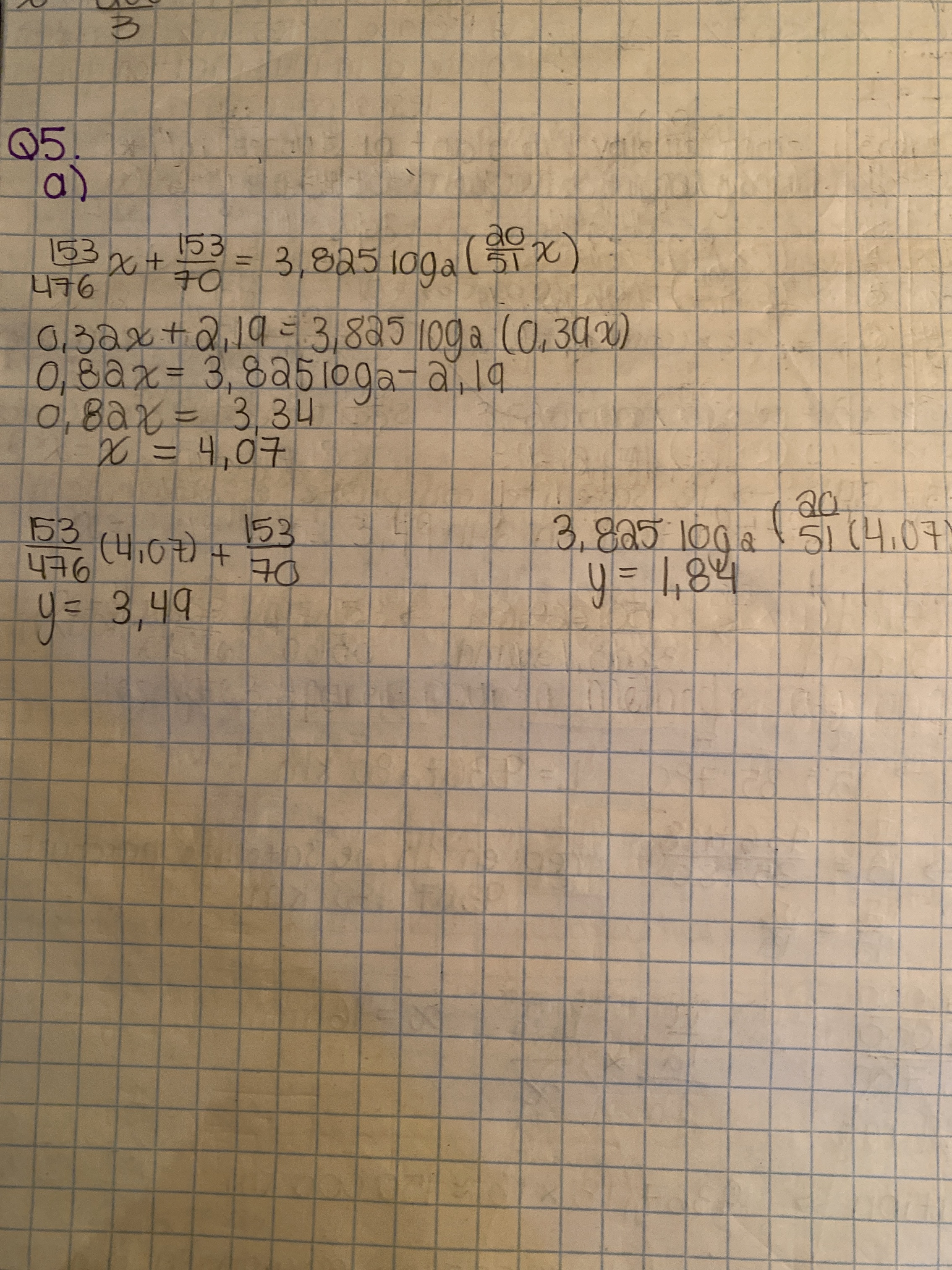
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

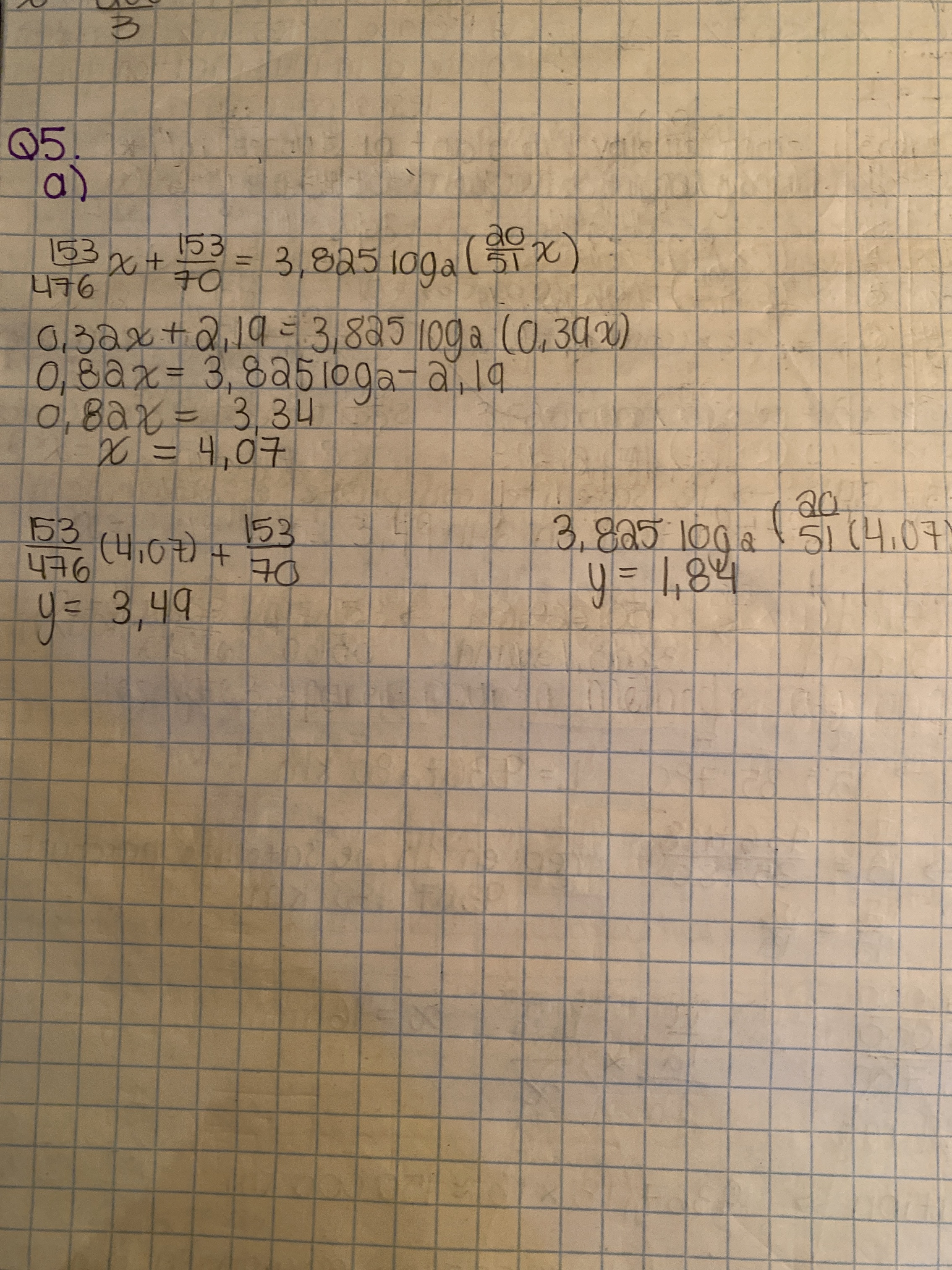






Pour rechercher le point de départ et le point de rencontre tu dois résoudre l'équation
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
que tu as bien commencé puis il y a eu des erreurs en cours de route
(puisque ils ont donné 3.825 à trois décimales après la virgule tu devrais arrondir à 3 décimales après la virgule).
ca donne
0.321 x +2.186 = 3.825 (log2 (0.392 x))
On convertit avec la regèle le log du produit en somme
log(ab)=log(a)+log(b)
log2(0.392 x)=log2(0.392)+log2(x)
Puis on calcule log2(0.392) par la machine à calculer on change la base 2 du log parce que les machines à calculer calculent le log en base 10
log2(0.392)=log10(0.392)/log10(2)
mais pour tout A positif on a log10(A)=log(A)
log(A) c'est l'opération que tu réalises avec la machine à calculer
log2(0.392)=log(0.392)/log(2) ici c'est le log c'est le log de la calculatrice
log2(0.392)=-0.407/0.301
log2(0.392)=-1.352
log2(0.392 x)=log2(0.392)+log2(x)
log2(0.392 x)=-1.352+log2(x)
l'équation devient:
0.321x+2.186=3.825(-1.352+log2(x))
0.321x+2.186=3.825(-1.352)+3.285 log2(x)
0.321x+2.186=3.825(-1.352)+3.285 log2(x)
0.321x+2.186=-5.171+3.285 log2(x)
0.321x+2.186+5.171=3.285 log2(x)
0.321x+7.357=3.285 log2(x) équation a résoudre
sauf qu'au programme on n'as pas étudié des équations du type
ax+b=c log(x)
Comme l'énoncé avait suggéré de faire un tableau de valeurs et comparer les deux expressions y1 et y2
On revient à la forme des coordonnes y1 et y2
y1=0.321 x +2.186
y2=3.825 (log2 (0.392 x))
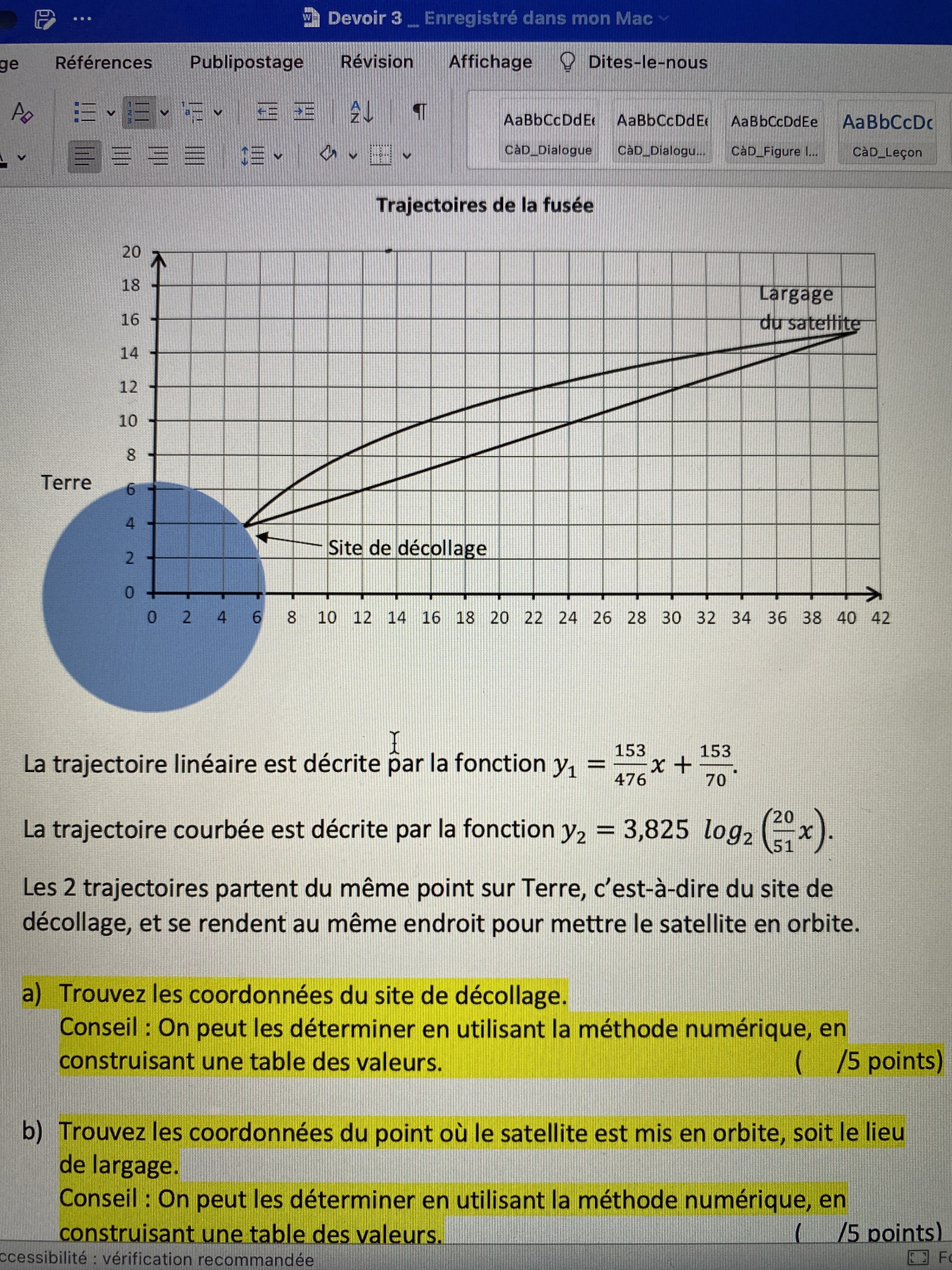
Selon le graphique le point de départ se situe proche de 5, on va calculer pour des valeurs de x autour de 5
On remplace x par 5 dans y1 et y2
y1=0.321 5 +2.186 ____________________ y1=3.791
y2=3.825 (log2 (1.960)) ,
y2=3.825(log(1.960))/(1og(2))___________ y2=3.714
On prend x=5.1
y1=0.321 5.1 +2.186_____________________y1=3.823
y2=3.825 (log2 (1.999)) ,
y2=3.825(log(1.999))/(1og(2))____________y2=3.825
y1 proche de y2
On peut prendre comme solution x =5.1
le site de décollage à pour coordonnées (5.1 , 3.825)
on voit bien sur la figure que l'ordonnée est proche de 4
Détermination du point de rencontre
Selon la figure x est proche de 41
x=41
y1=0.321 41 +2.186___________________y1=15.347
y2=3.825 (log2 (0.392 41))_____________y2=15.327
x=40.9____________________________y1=15.315
_________________________________y2=15.315
le largage du satellite se fera au point de coordonnées (40.9 , 15.315)
c'est cohérent avec la figure présentée
Explication d'Alloprof
Cette explication a été donnée par un membre de l'équipe d'Alloprof.
Bonsoir OursTenace2267,
Lorsque tu es en forme logarithmique, il doit toujours y avoir un argument.
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Ainsi, tu n'as pas le droit de l'annuler comme s'il ne représentait qu'une simple multiplication et laisser le log vide. Tu dois donc recommencer ton calcul. De plus, je te conseille de ne pas arrondir tout de suite.
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
N'hésite pas à nous recontacter si tu as d'autres questions!
Suggestions en lien avec la question
Suggestion en lien avec la question
Voici ce qui a été trouvé automatiquement sur le site, en espérant que ça t’aide!