Best Of
Question
Hello, I still spend time on the computer to play and study games (especially educational games) but my parents think that I am just having fun. Is there a good way to explain to them that I am not kidding ???
Re: Question
voici les definition
- (CHEZ LES HUMAINS)
- Conformation particulière qui distingue l'homme de la femme en leur assignant un rôle déterminé dans la reproduction.
- Enfant de sexe masculin, féminin.
- 2.
- (CHEZ LES HUMAINS)
- Qualité d'homme ou qualité de femme.
- L'égalité des sexes.
Question
L'examen dure 3h en tous, 1h pour chaque examen. Si j'ai 60 questions à répondre pour 1h, sa veut dire je dois prendre 1 minutes pour chaque questions, comment je fais pour faire plus vite?
Question
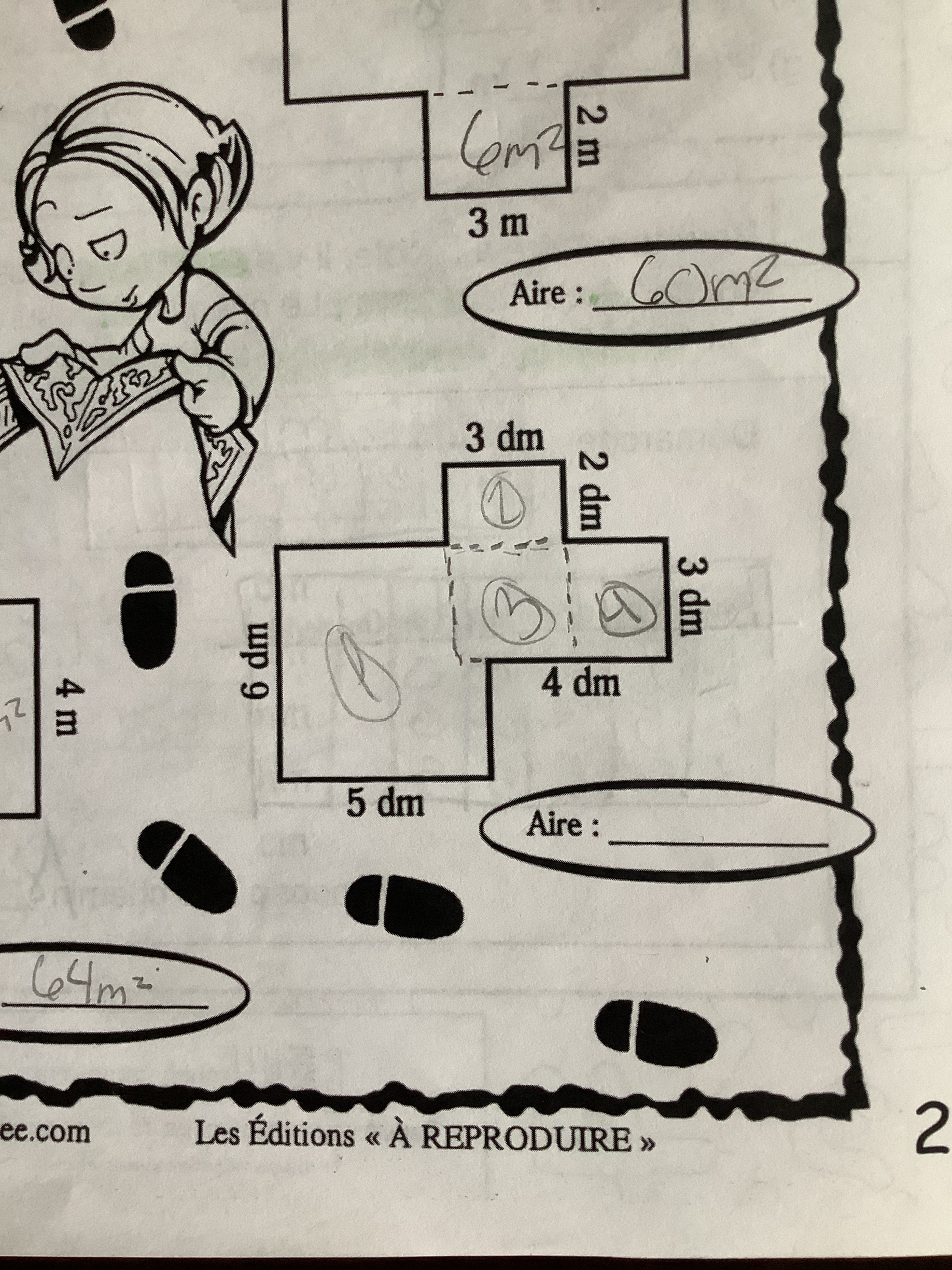
Salut! J’aimerais vous poser une question. Dans la photo ci-dessous, à la dernière forme, je ne comprends pas comment faire pour calculer l’aire. Je sais comment, mais je bloque dès que je vois cette forme complexe. Pouvez-vous m’aider s’il te plaît 🙏?
Merci en avance!
Question
Bonjour Alloprof,
Est-ce-que vous pouvez m'expliquer les quatres forces du vol?
Merci
Re: Question
Allo GiganotosaureRouge6194,
Merci pour ta question!
Oui, je crois que tu as la bonne réponse et ce que l'on cherche!
Continue comme ça!
Lea-Kim
Question
Je ne comprends pas cet exercice:
321 684= ? UM +16 C+ ? d+ ? unités
est-ce qu'on peut dire:
= 321 UM + 16C + 32168 d + 321684 u ?
Re: Question
Bonjour,
Mensuel signifie chaque mois. Par exemple, si tu reçois un magazine mensuel, cela veut dire que tu reçois ce magazine une fois par mois. De même, si on parle d'un paiement mensuel, c'est un montant que tu paies chaque mois.