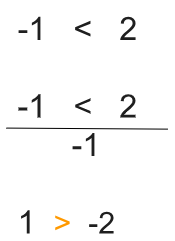Best Of
Re: Question
Je vais t'expliquer les proportions directes et inverses, ainsi que leur représentation sur des graphiques, de manière simple :
1. Proportion directe :
Dans une proportion directe, deux grandeurs augmentent ou diminuent ensemble. Autrement dit, quand l'une des quantités augmente, l'autre augmente aussi proportionnellement.
- Formule mathématique :
- y=k⋅xy = k \cdot xy=k⋅x (où kkk est une constante).
- Exemple : Si tu achètes plus de pommes, tu paies plus cher. Si une pomme coûte 2 €, alors si tu en achètes 3, tu paieras 6 € (3 pommes × 2 €/pomme = 6 €).
- Graphique :
- Sur un graphique, une proportion directe est représentée par une ligne droite qui part du point (0,0) et monte en diagonale. Plus la constante kkk est grande, plus la pente de la ligne est raide.
2. Proportion inverse :
Dans une proportion inverse, quand une grandeur augmente, l'autre diminue proportionnellement. C'est l'opposé de la proportion directe.
- Formule mathématique :
- y=kxy = \frac{k}{x}y=xk (où kkk est une constante).
- Exemple : Si 4 personnes construisent une maison en 10 jours, alors 2 personnes prendraient 20 jours pour faire le même travail. Plus il y a de personnes, moins de temps il faudra pour terminer la tâche.
- Graphique :
- Sur un graphique, une proportion inverse est représentée par une courbe descendante qui ne touche jamais les axes. La courbe diminue plus rapidement au début, puis elle devient plus plate à mesure que xxx augmente.
Visualisation sur un graphique :
- Proportion directe : Graphique :Une droite diagonale qui part du point (0,0) et monte reˊgulieˋrement.\text{Graphique :} \quad \text{Une droite diagonale qui part du point (0,0) et monte régulièrement.}Graphique :Une droite diagonale qui part du point (0,0) et monte reˊgulieˋrement.
- Cela montre que chaque augmentation de xxx entraîne une augmentation de yyy à un rythme constant.
- Proportion inverse : Graphique :Une courbe qui descend en se rapprochant de l’axe des x, mais sans jamais l’atteindre.\text{Graphique :} \quad \text{Une courbe qui descend en se rapprochant de l'axe des x, mais sans jamais l'atteindre.}Graphique :Une courbe qui descend en se rapprochant de l’axe des x, mais sans jamais l’atteindre.
- Cela montre que lorsque xxx augmente, yyy diminue.
Re: Question
Salut!
C'est parce que, lorsqu'on divise un nombre avec un nombre négatif, ce dernier subit un changement de signe. Il faut lui inverser son signe (ex: diviser un nombre positif par un nombre négatif = réponse négatif). Donc, nbr+/nbr- = nbr- et nbr-/nbr- = nbr+.
Dans ce même sens, lorsqu'on divise les nombres d'une inéquation par un nombre négatif, le signe de l'inéquation (le symbole) subit également un inversement de signe, d'où le corrigé.
Je te donne un exemple:
Dans l'exemple, on voit clairement que, une fois qu'on divise l'inéquation par -1 pour isoler le 1, l'inéquation initiale s'inverse. 1 devient supérieur à -2. Au final, l'inéquation initiale n'est plus vraie donc il faut inverser le signe "inférieur" pour "supérieur.
J'espère que ça t'aide un peu! :D
Re: Question
Bonsoir, si je ne me trompe pas, le comportement des particules dépend de la température. En effet, plus la température est élevé , plus les particules seront agitées. Dans ce cas-ci tu dois donc comparé le degré d'agitation des particules d'eau froide et d'eau chaude. Les particules seront donc plus agitées dans un bécher d'eau chaude comme je l'ai expliqué au début et moins agitées dans un d'eau froide. Tu peux aussi trouver les explications sur ce concept si tu recherches '' La température'' dans la barre de recherche sur Alloprof.
Re: Question
Salut!
Un changement physique est une transformation qui ne change pas la nature de la substance. En d'autres mots, les propriétés de la matière restent les mêmes, même si son apparence, sa forme ou son état (solide, liquide, gaz) change. Par exemple, la glace qui fond en eau est un changement physique, car l'état change, mais cela reste toujours la même substance.
À l'inverse, un changement chimique modifie la composition chimique de la substance, c'est-à-dire que de nouvelles substances sont créées et qu'il est généralement impossible de revenir en arrière facilement. Par exemple, le bois qui brûle et devient de la cendre est un changement chimique, tout comme le fer qui rouille lorsqu'il y a de l'humidité.
En résumé, la substance reste la même lorsqu'il y a un changement physique, tandis qu'une nouvelle substance est créée lorsqu'il y a un changement chimique.
Voici des fiches sur ces notions pour plus d'exemples :
Si tu as d'autres questions, n'hésite pas à nous réécrire! :)
Re: Question
Salut!
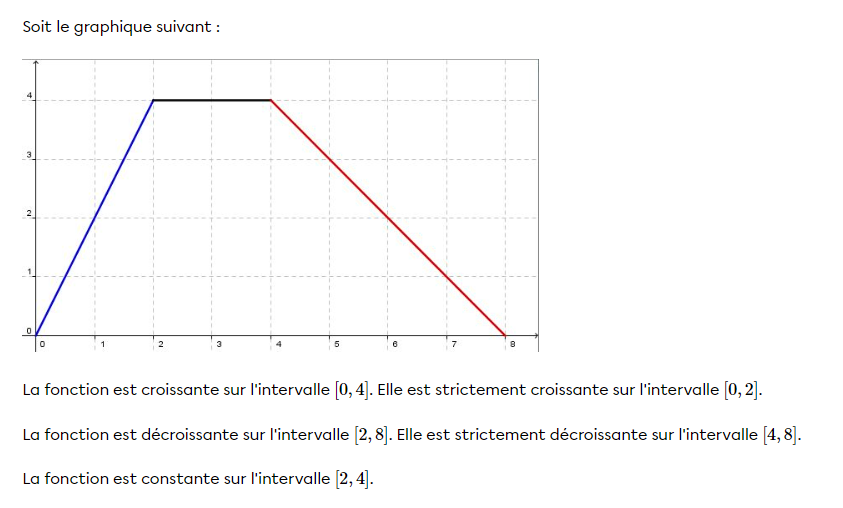
La variation fait référence à la croissance et à la décroissance d'une fonction.
La croissance est l'intervalle en x pour lequel la courbe est croissante, c'est-à-dire que plus on avance dans l'axe des x, plus la valeur en y augmente. Voici un exemple :
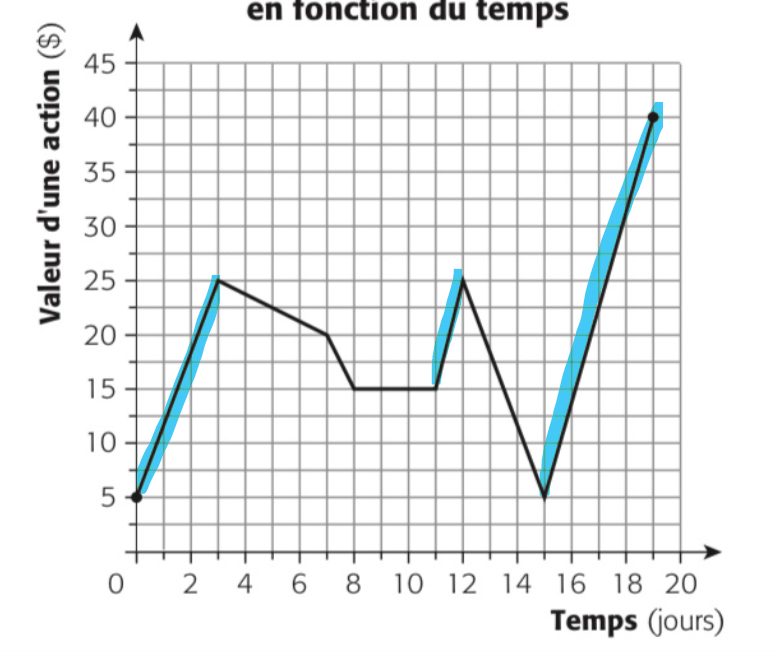
Pour ton exercice, la fonction est strictement croissante sur cet intervalle :
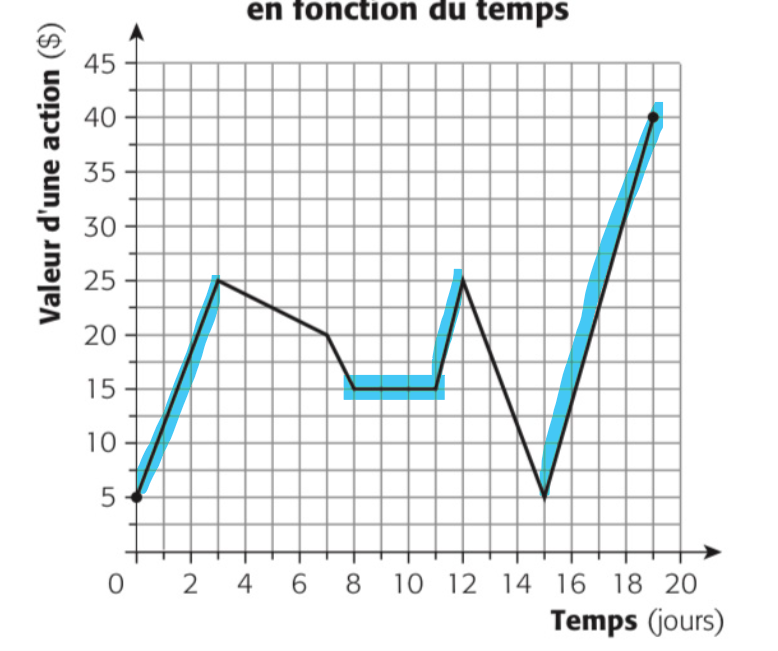
Et croissante sur cet intervalle (on ajoute la partie constante) :
Tu dois unir tes portions d'intervalles à l'aide du symbole d'union ∪. Par exemple, l'intervalle où la fonction est croissante est : [0, 3] ∪ [8, 12] ∪ [15, 19].
Je t'invite à consulter la fiche suivante, on y explique justement les différentes propriétés des fonctions : Les propriétés des fonctions | Secondaire | Alloprof
Je te laisse essayer avec ces indices. Si tu as d'autres questions, n'hésite pas à nous réécrire! :)
Re: Question
Salut FraiseAdorable5247 😁
Merci pour ta question!
On veut que tu expliques, grâce au modèle particulaire, la position des particules les unes par rapport aux autres, puis à l'aide des mouvements possibles des particules, dépendamment des états de la matière.
Voici deux images qui pourront t'aider à former ton explication.
Modèle particulaire :
Mouvements des particules :
Solid = solide
Liquid = liquide
Gas = gaz
Vibrational = vibration
Rotational = rotation
Translational = translation
Écris-nous si tu as d'autres questions. 😊
À bientôt sur la Zone d'entraide! 😎
Re: Question
Bonjour!
Dans cet exercice, tu dois ajouter deux adjectifs ou plus aux mots qui sont soulignés dans les phrases. On indique que tu peux utiliser les adjectifs dans le tableau ou des adjectifs de ton choix.
Voici un exemple :
Julie has a pair of shoes.
Julie has a beautiful pair of pink shoes. -> j'ai ajouté les adjectifs « beautiful » et « pink » au mot « shoes » afin de rendre la phrase plus intéressante.
À ton tour d'essayer! :D
Si tu as d'autres questions, n'hésite pas à nous réécrire. Nous te répondrons avec plaisir!
Laurie :)
Re: Question
Salut ArgentEfficace9281 😁
Merci pour ta question!
La masse représente la quantité de matière d’une substance ou d’un objet. Elle se mesure généralement en grammes (g).
Le poids d’un objet représente la mesure de la force avec laquelle la Terre (ou un autre astre) l’attire vers elle. Le poids se mesure en newtons (N).
Apprends-en plus grâce à cette vidéo!
Pour des exercices, c'est par ici.
Écris-nous si tu as d'autres questions. 😊
À bientôt sur la Zone d'entraide! 😎
Re: Question
Bonjour TitanZen1250 !
Merci d'avoir utilisé la zone d'entraide d'Alloprof.
Le mot «nulle» peut appartenir à différentes classes de mots dépendamment du contexte où il est utilisé. Il peut être un adjectif, un pronom ou encore un déterminant.
Voici une fiche pour t'aider : https://www.alloprof.qc.ca/fr/eleves/bv/francais/les-classes-de-mots-primaire-f1710
J'espère t'avoir aidé !