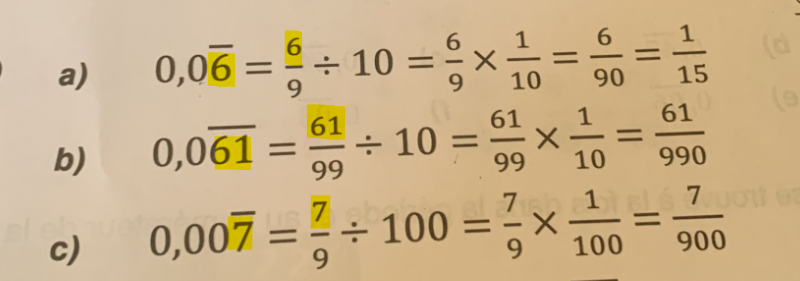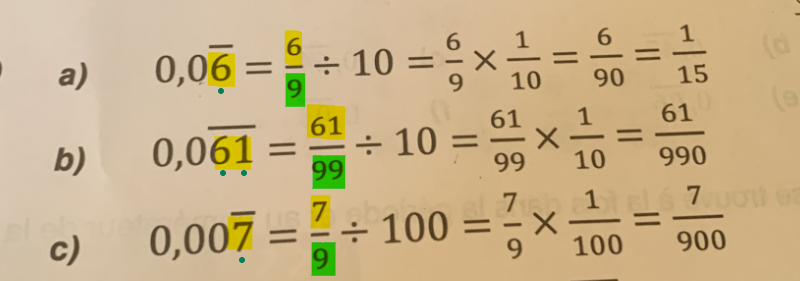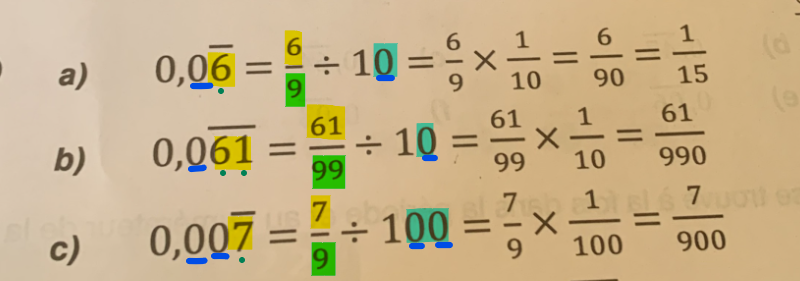Best Of
Re: Question
Bonjour à toi!
Merci pour ta question :)
En effet, ça peut être un choix difficile de changer ou non de programme. Malheureusement, il n'y a pas de bonne ou de mauvaise réponse que nous pouvons te donner!
Mon conseil, c'est d'y aller avec le programme qui t'intéresse le plus. Si c'est LLS, fonce! Il y a toujours des moyens de rattraper des notions que tu n'aurais pas vues en allant à des récupérations ou en parlant à ton enseignant.e.
J'espère que ça peut t'éclairer!
Bonne journée :D
Ariane
Re: Question
Salut LokoriSigma1332!
Merci pour ta question. :)
C'est une super recommandation que tu as là! Je t'invite à la partager directement avec l'équipe technique d'Alloprof en cliquant sur le lien suivant!
Merci pour ton intérêt envers nos jeux!
À bientôt,
Océane :)
Re: Question
Allo MonarqueArtistique5819,
Merci pour ta question!
Les deux options fonctionnent. La multiplication est commutative, tu peux donc la faire dans l'ordre que tu veux.
J'espère t'avoir aidé!
Lea-Kim
Re: Question
Salut!
On te présente une façon de transformer un nombre périodique en fraction. Pour cela, tu dois suivre ces étapes :
1) Identifie le nombre formé par les chiffres où la période est appliquée. Place ce nombre au numérateur.
2) Si ce nombre est formé de 1 chiffre, alors divise-le par 9. S'il est formé de 2 chiffres, divise-le par 99. S'il est formé de 3 chiffres, divise-le par 999. Etc.
3) Dans le développement décimal, trouve le nombre de zéros devant la partie périodique. Cela te permettra de déterminer le multiple de 10 par lequel tu dois diviser. Par exemple, en a) et b), il y a 1 zéro devant les 6, donc on divise par 10. En c), il y a 2 zéros, donc on divise par 100. S'il y avait 3 zéros, on diviserait par 1000. Etc.
4) Tu peux ensuite transformer la division en multiplication par l'inverse, puis effectuer la multiplication de fraction pour trouver la fraction finale équivalente au nombre périodique de départ.
Pour le numéro J), n'oublie pas de considérer la partie entière à la fin. Si tu effectues seulement les étapes 1 à 4 décrites plus haut, tu obtiendras le nombre fractionnaire. Tu peux ensuite transformer ce nombre fractionnaire en fraction si tu le souhaites.
Voici une fiche où tu trouveras une méthode alternative pour transformer un nombre périodique en fraction : De la fraction au nombre périodique et l'inverse | Secondaire | Alloprof
J'espère que c'est plus clair pour toi! Si tu as d'autres questions, n'hésite pas à nous réécrire! :)
Re: Question
Allo MonarqueArtistique5819,
Merci pour ta question!
Oui, ce sont bel et bien des termes semblables. Pour les calculer, on doit seulement les mettre ensemble. On fera donc:
-y-3/5y
Et on obtient : -8/5y
J'espère t'avoir aidé!
Lea-Kim
Re: Question
Salut!
Un terme est un synonyme de mot. Ainsi, trouver un terme dans un texte signifie que l'on cherche à localiser un mot spécifique au sein du texte. Par exemple, si on te demande de trouver le terme "nature" dans un texte, tu dois localiser où ce mot est mentionné.
Si tu as d'autres questions, n'hésite pas à nous réécrire! :)
Re: Question
Salut!
Le signe des coefficients n'est pas un facteur à considérer pour déterminer si deux termes sont semblables ou non. Des termes sont semblables lorsqu’ils ont les mêmes variables (les mêmes lettres) affectées des mêmes exposants.
Ainsi, -2x² et 7x² sont bien des termes semblables, puisqu'ils ont tous deux la variable \(x\) affecté du même exposant, soit 2!
Voici une fiche sur cette notion qui pourrait t'être utile : Algèbre - Expressions algébriques | Alloprof
Si tu as d'autres questions, n'hésite pas à nous réécrire! :)
Re: Question
Salut PerleAimable1529 😁
Merci pour ta question!
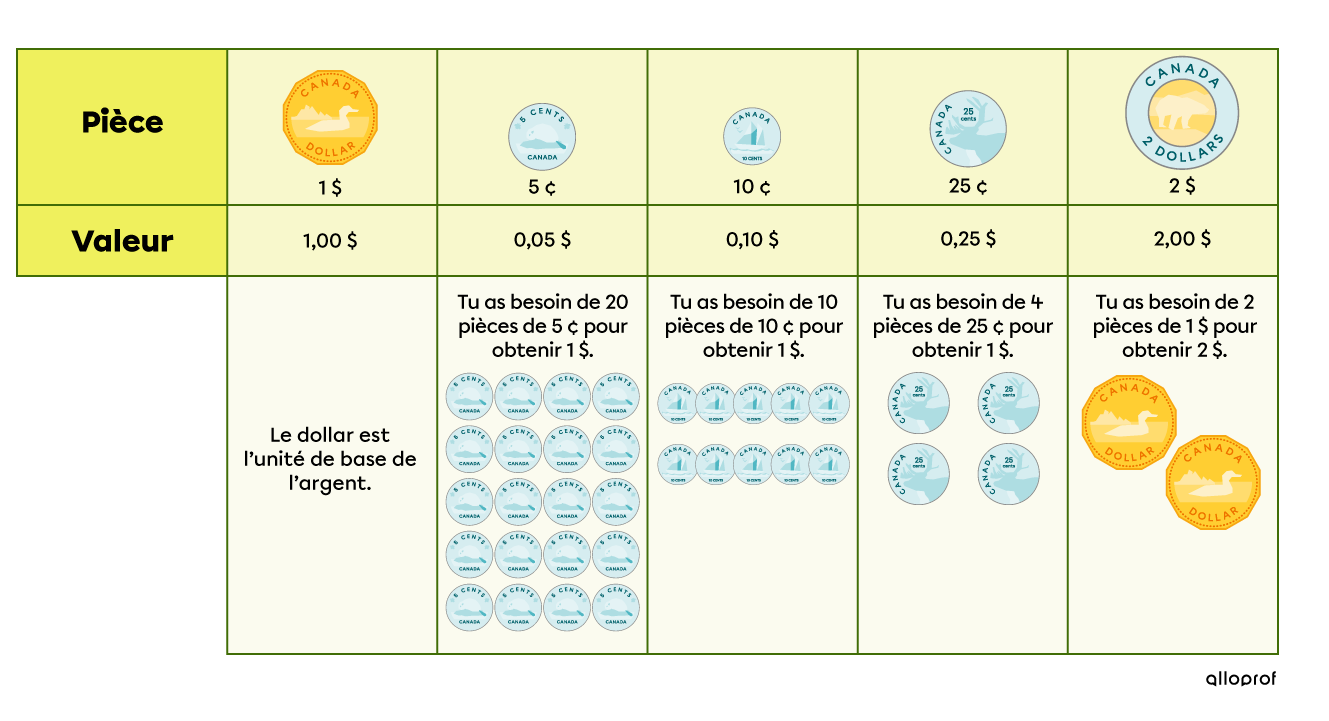
Tu peux faire un rectangle avec un 10$ à l'intérieur, ton enseignant.e comprendra ce que tu as voulu illustrer. Pour les pièces, tu peux faire des cercles avec la valeur inscrite à l'intérieur, comme pour le rectangle.
Voici la liste des billets et des pièces au besoin.
Tu savais qu'il y a déjà eu des billets de 1$, 2$, 25$, 500$ et même de 1 000$ au Canada? Ils n'existent plus aujourd'hui.
Tu peux en voir d'autres modèles ici si ça t'intéresse!
N'hésite pas si tu as d'autres questions 😊
À bientôt 😎