Best Of
Re: Question
Salut!
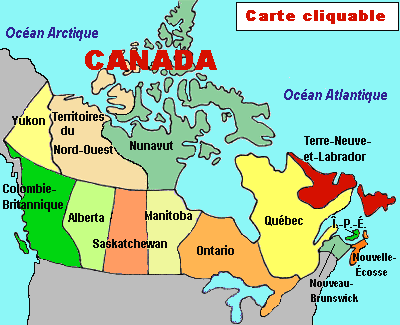
Le Canada est composé de 10 provinces : la Colombie-Britannique, l'Alberta, la Saskatchewan, le Manitoba, l'Ontario, le Québec, le Nouveau-Brunswick, l'Île-du-Prince-Édouard, la Nouvelle-Écosse et Terre-Neuve-et-Labrador, et de 3 territoires : le Yukon, les Territoires du Nord-Ouest et le Nunavut.
Si tu as d'autres questions, n'hésite pas à nous réécrire! :)
Question
Quel appareil fonctionne grâce à la dilatation des solides ? Et quel appareil fonctionne grâce à la dilatation des liquides ?
Re: Question
Bonjour,
Tu peux jouer à Potager en péril sur un Ipad, tu dois seulement t'assurer d'avoir l'application (disponible sur Apple store). Si tu essaies de jouer à ce jeu à partir d'internet, les commandes ne fonctionneront pas.
N'hésite pas à nous réécrire si tu as d'autres questions! :)
Karen
Re: Question
Bonjour! :) Merci pour cette excellente question!
En fait, après quelques recherches, j'ai découvert que le orange est un symbole qui représente une expérience que Phyllis (Jack) Webstad (la personne qui a eu l'idée de cette journée) a vécu.
En effet, lorsque Phyliss était enfant, elle portait un chandail orange pour sa première journée d'école à un pensionnat missionnaire (qui avait pour but de convertir les autochtones). On y déshabillait les enfants de force, donc on lui a enlevé et confisqué son chandail orange.
Le chandail orange renvoie donc à la déshumanisation dont plusieurs personnes autochtones ont été victimes.
J'ai trouvé plusieurs articles à ce sujet, mais ils sont malheureusement en anglais. Si tu veux, tu peux quand même essayer de les lire ou les montrer à tes parents. :)
https://canadiangeographic.ca/articles/survivor-the-story-of-phyllis-webstad-and-orange-shirt-day/
J'espère que ça t'aide un peu! :)
Sarah G
Re: Question
c'est a propos des premières nations et pour les supporter il faut mettre un shirt orange.
Re: Question
Bonjour!
Afin de savoir comment les bébés grandissent et naissent, je te suggère de consulter la fiche ci-dessous! Elle explique la fécondation, la grossesse et l'accouchement! :)
Ces concepts scientifiques sont un peu avancés pour la 6e année. Il est possible que tu ne comprennes pas tout, c'est normal! :D
Si tu as d'autres questions, n'hésite pas à nous réécrire. Nous te répondrons avec plaisir!
Laurie :)
Re: Question
Salut ElfeSage8923!
Merci pour ta question. :)
Il existe plusieurs façons différentes de déterminer le résultat de cette multiplication.
Je te suggère de procéder avec la méthode de multiplication par colonne! Pour t'aider, je te conseille fortement le visionnement de cette vidéo qui t'accompagnera étape par étape dans ton calcul! :D
En espérant que cela répond à ta question. Si tu en as d'autres, n'hésite surtout pas à nous réécrire, il nous fera plaisir de t'aider à nouveau!
À bientôt,
Océane :)
Re: Question
Allo ElfeSage8923!
Pour faire cette multiplication il suffit de faire ceci:
35
x 9
____
315
- Fait tout d'abord le 5 du 35 x 9 = 5x9 qui donne 45.
- Tu écrit 5 en bas de la lignes puis tu mets une retenue de 4 au 3
- Puis 3x9 qui donne 27 tu fera donc à ce moment un calcul mental qui ressemblera à ceci: 27+4= 31
- Tu écris le 31avant le 5 pour faire la réponse de 315!
Re: Question
Bonjour!
Afin de bien comprendre les nombres premiers, je te suggère de consulter la fiche ci-dessous. Elle contient même une vidéo qui explique très bien les nombres premiers! :D
Si tu as d'autres questions, n'hésite pas à nous réécrire. Nous te répondrons avec plaisir!
Laurie :)