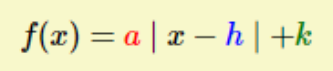Best Of
Re: Question
Bonsoir! :) Nous sommes heureux de savoir que tu apprécies nos services! :)
Les raisons derrières la rébellion des treize colonies sont nombreuses. Toutefois, les deux principales sont économiques et politiques:
- La Grande-Bretagne impose plusieurs taxes (Sugar Act, Tea Act, Stamp Act, Townshend Act)
- No taxation without representation : On taxe, mais les Treize Colonies n'ont pas de représentant au parlement.
Ils sont donc très fâchés.
On t'explique la Révolution américaine dans la vidéo suivante (la vidéo se trouve en bas de la fiche): https://www.alloprof.qc.ca/fr/eleves/bv/histoire/la-revolution-americaine-mise-en-contexte-h1471
Bon visionnement! J'espère que ça t'aidera!
N'hésite pas à revenir nous poser tes questions! Il nous fait toujours plaisir de t'aider! :)
Sarah G
Re: Question
Salut PicComique9971 😁
Merci pour ta question!
C'est un pic-bois qui est comique.
Sous la forme canonique, voici où se situe les différents paramètres.
Alors, pour ta fonction, on doit remettre dans l'ordre affiché ci-haut. On effectue donc quelques changements.
$$f(x)= -2 \left[4-x\right] -9;$$
On commence par remettre x en avant en l'interchangeant avec ce qui lui est additionné ou soustrait (ici +4).
$$f(x)= -2 \left[-x+4\right] -9;$$
Ensuite, on le rend positif avec une simple mise en évidence.
$$f(x)= -2 \left[-1(x-4)\right] -9.$$
Maintenant, on a le b et le h très visibles, sous la forme canonique.
Écris-nous si tu as d'autres questions. 😊
À bientôt sur la Zone d'entraide! 😎
Re: Question
Salut !
Comme l'examen est demain, tu peux en effet revoir les notions clés, mais je suggère une bonne nuit de repos pour pouvoir être à ton meilleur lors de l'examen !
Mais en général, la pratique est la meilleur manière de retenir des concepts et de les maîtriser.
Je te souhaite un bon courage pour ton examen de demain et si tu as d'autres questions, n'hésite pas !
Bonne soirée !
Re: Question
Salut !
En effet la racine carrée d'un nombre réel ne peut pas être négative.
J'espère que cela ait pu t'aider et si tu as d'autres questions, n'hésite pas !
Bonne soirée !
Re: Question
Bonsoir! :) Merci pour ta question!
Tu trouveras deux exercices synthèses en bas de la fiche suivante: https://www.alloprof.qc.ca/fr/eleves/bv/francais/les-classes-de-mots-f1178
On y demande d'identifier les classes de mots. Tu as plusieurs choix, dont les adverbes, les conjonctions et les prépositions.
Voici des exercices plus précis:
- Sur l'adverbe
- Sur la conjonction
- Sur la préposition
Nous n'avons pas d'exercices de différentiation en tant que tels, mais les exercices que je t'ai proposés ci-haut te permettront de mieux comprendre en quoi consiste chacune de ces classes de mots invariables.
Je te donne toutefois des explications et des trucs pour les différencier dans la réponse suivante: https://www.alloprof.qc.ca/zonedentraide/discussion/64026/question/p1
Voilà! :) Bonne révision! N'hésite pas si tu as d'autres questions!
Sarah G
Re: Question
va sur récitus primaire. com sur se site tu pourras avoir tout ses info
Re: Question
Non ce n'est pas pour ça se sont les familles françaises qui se sont installer à la nouvelle France les nouveaux nés qui on peuplé le territoire mes avant sa nous avons crée Québec ville-marie=Montréal et trois rivières j'espère que l'information ta aidé bonne journée à toi''
Re: Question
Salut!
Tu dois te servir du paramètre \(k\) et du signe du paramètre \(a\) pour trouver l'image.
Le paramètre \(k\) est la coordonnée en y du sommet de la fonction.
De plus, si le paramètre \(a\) est positif, alors la fonction est ouverte vers le haut, tandis que s'il est négatif, la fonction est ouverte vers le bas.
L'image de la fonction est donc :
Si tu as d'autres questions, n'hésite pas à nous réécrire! :)
Re: Question
Allo CobraAgile3504,
Merci pour ta question!
Il y a plusieurs innovations! Autant dans la communication, le transport ou la conquête de l'espace.
Nous avons une fiche qui les regroupe! Je t'invite à la consulter: https://www.alloprof.qc.ca/fr/eleves/bv/histoire/technologies-20e-siecle-h1123
J'espère t'avoir aidé!
Lea-Kim
Re: Question
Bonjour OrDelta7782! Une question éthique est une question dont la réponse n'est pas prédéterminée. Cette réponse va varier d'une personne à l'autre selon ses valeurs, ses croyances, ses opinions, etc. Une question éthique amène à réfléchir, à faire des liens. C'est souvent un sujet de débat. J'espère t'avoir aidé.e!