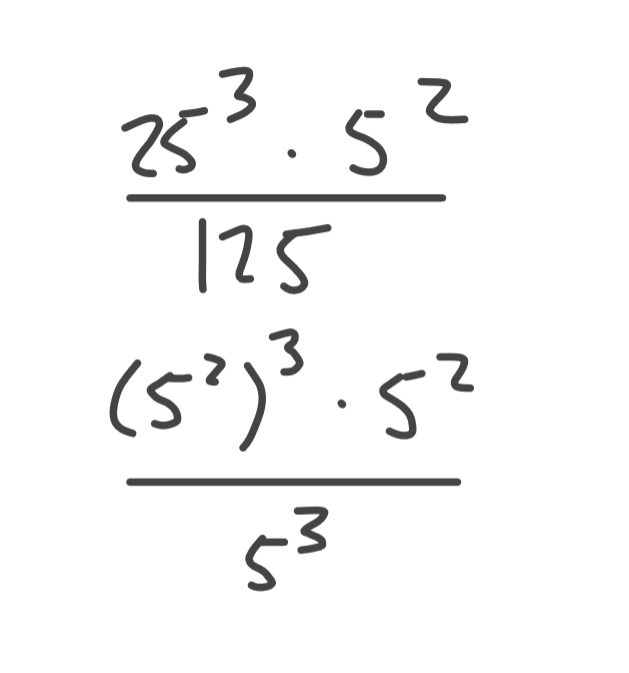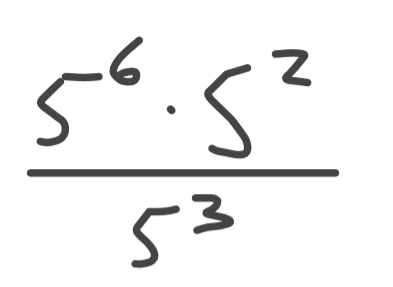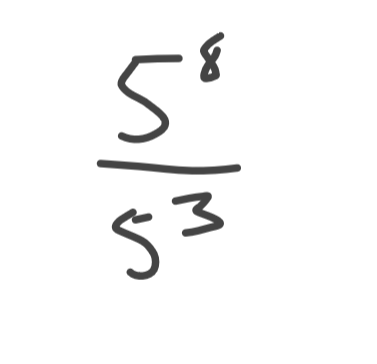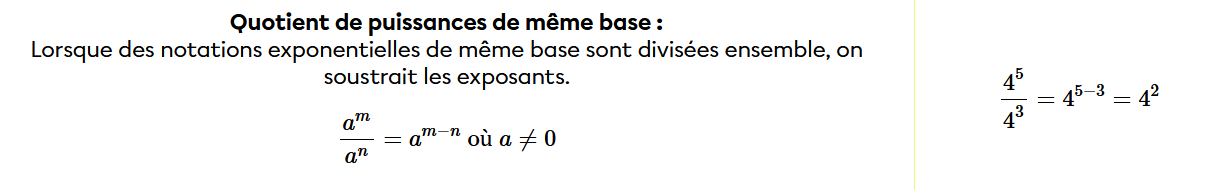Best Of
Re: Question
Bonjour!
Les sous-aspects sont des aspects contenus dans un paragraphe d'aspect.
Par exemple, dans le paragraphe d'aspect 3, on retrouve deux sous-aspect : on aborde l'habitat du dinosaure ainsi que son alimentation! :)
Je te suggère de consulter la fiche ci-dessous. Elle explique bien les aspects et les sous-aspects et donne de nombreux exemples! :D
Si tu as d'autres questions, n'hésite pas à nous réécrire. Nous te répondrons avec plaisir!
Laurie :)
Re: Question
1+1 Tu doit ajouter un 1 , la deuxième stratégie c'est tu dois compter compte 1 ...
Re: Question
Salut ChevalOrange615 😁
Merci pour ta question!
On peut commencer par tout mettre à base 5.
Ensuite, on réduit le plus possible en utilisant ces lois des exposants.
N'hésite pas à réviser les lois des exposants par ici.
Écris-nous si tu as d'autres questions. 😊
À bientôt sur la Zone d'entraide! 😎
Re: Question
Tu dois utiliser la plus petite base possible.
Quel chiffre multiplié plusieurs fois donne 27? Quels sont les diviseurs de 27? Quel est le plus petit?
Re: Question
Allo OnyxRose3352,
Merci pour ta question!
Il est vrai que les mathématiques peuvent sembler plus difficile pour certains. Par contre, comme toutes les autres matières, ça devient plus facile avec de la pratique. Je te conseille donc de te pratiquer à faire des mathématiques et tu verras, ça va devenir plus simple.
Si tu as des questions ou besoin d'exercices supplémentaires, n'hésite pas à nous écrire.
J'espère t'avoir aidé!
Lea-Kim