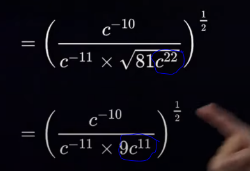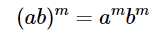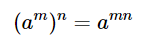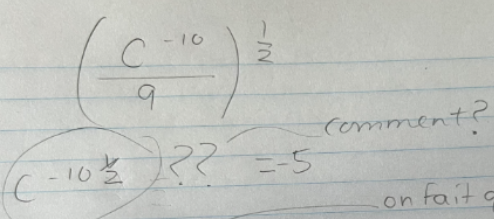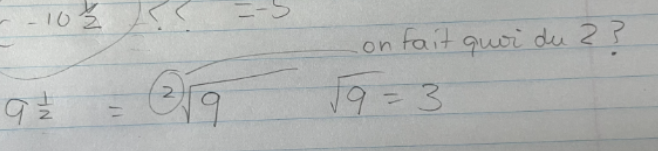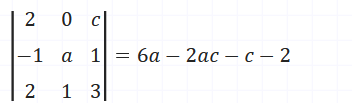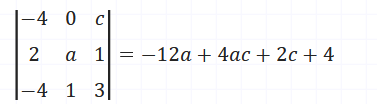Best Of
Re: Question
Salut!
Ici :
La racine carrée peut se réécrire en exposant fractionnaire 1/2 grâce à cette loi des exposants :
On a donc :
$$ \sqrt{81c^{22}}$$
$$ (81c^{22})^{ \frac{1}{2} }$$
L'exposant se distribue sur chaque facteur :
$$ (81)^{\frac{1}{2}}(c^{22})^{\frac{1}{2}}$$
La racine carrée de 81 est 9 :
$$ 9(c^{22})^{\frac{1}{2}}$$
Puis, on peut multiplier les exposants 22 et 0,5 selon cette loi des exposants :
Ce qui nous donne un exposant de 11, car \(22 \times \frac{1}{2}=11\):
$$ 9c^{11}$$
En ce qui concerne ta seconde question, tu dois appliquer les lois des exposants encore une fois.
Ici, tu as l'exposant -10 × ½. Le résultat de cette multiplication est -5, donc :
$$ c^{-10 × \frac{1}{2}} = c^{-5}$$
Une racine carrée peut s'écrire comme ceci \( \sqrt{}\) ou comme ceci \( \sqrt[2]{}\), c'est la même chose! ;) Il faut écrire l'indice lorsqu'il est différent de 2 seulement, donc lorsqu'on a une racine cubique, une racine quatrième, une racine cinquième, etc.
Voilà! J'espère que c'est plus clair pour toi! :)
Re: Question
Salut!
Les nombres premiers sont des nombres divisibles que par 1 ou eux-même. Ex: 1, 3, 7 etc
Un nombre carré est un nombre qui est le résultat d'une multiplication de deux nombres pareils. Ex: 1x1=1, 2x2=4, 3x3=9, 4x4=16
La somme (le total) doit être inférieur ou égal à 25.
Re: Question
Salut WasabiComique8746😁
Merci pour ta question!
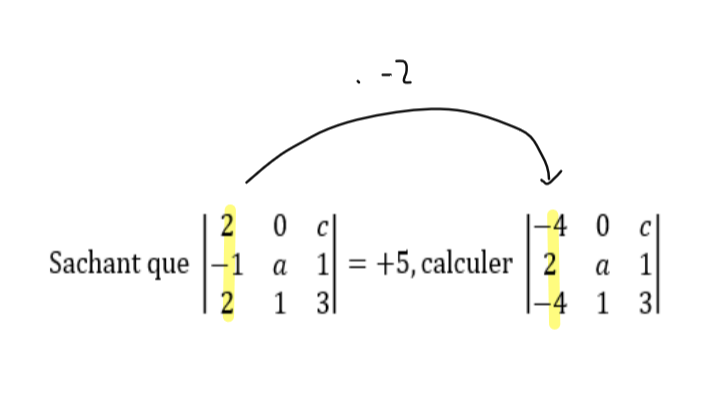
Les matrices!
Comme on peut le voir, ici, on multiplie par -2.
Le déterminant de la première matrice est 6a - 2ac - c - 2 = 5.
Le déterminant que la deuxième matrice est -12a + 4ac + 2c +4. On peut donc sortir le *-2, qu'on avait remarqué au début (avec une simple mise en évidence).
-2 (6a - 2ac - c - 2)
On peut substituer par 5 l'expression de départ, le déterminant de la première matrice.
On a alors -2*5= -10. Cela veut dire que le déterminant de la deuxième matrice est égal à -10.
N'hésite pas si tu as d'autres questions 😊
À bientôt 😎
Re: Question
Salut !
Merci de faire appel au service d'Alloprof ! Dans ce genre d'exercice, il est pertinent de dessiner un schéma de la situation. Ta situation ressemble à la suivante :
Si la boîte est en MRU, cela implique que la vitesse est constante. Et à vitesse constante, la somme des forces est nulle. Pour te simplifier le calcul, tu peux calculer cette somme en un seul axe, celui du mouvement.
$$ F_{x, totale}=F_{x, frottement}+F_{x, tension} $$
La force de frottement se calcul à l'aide de la force normal. Dans ton cas, la force normale se calcule à l'aide de la force gravitationnelle.
$$ F_f=\mu \cdot F_N $$
J'espère que cela ait pu t'aider et si tu as d'autres questions, n'hésite pas !
Bonne soirée !
Re: Question
Bonjour SaturneCandide5365!
Bienvenue dans la Zone.
C'est une très belle question que tu nous soumets là! Idéalement, tu dois d'abord tracer ton diagramme de corps libre pour bien visualiser toutes les forces en présence. Au besoin, consulte cette fiche... https://www.alloprof.qc.ca/fr/eleves/bv/physique/les-diagrammes-de-corps-libre-p1091
Ensuite, tu dois bâtir les 2 équations des forces, en "x" et en "y". Puisque la caisse va se mettre en mouvement aussitôt que la composante de la tension en "x" va surpasser la valeur de la force de frottement, la FRx vaut donc 0 N. La FRy également, puisque la caisse ne se déplace pas à la verticale.
Tu auras également besoin de la formule qui exprime la relation entre la force de frottement, la force normale et le coefficient de frottement. Tu vas la trouver dans cette fiche ...
Finalement, tu devras résoudre le système à deux équations (FRx et FRy) et deux inconnues (T et FN).
Avec ces informations, tu devrais être en mesure de trouver les valeurs de T (la tension dans la corde) et de FN (la force normale).
Merci d'avoir fait appel à nos services.
Bonne soirée.
Re: Question
Pour les arguments, il y a la technique OREO:
O: Opinion
R: Raison
E: Exemple ou explication
O: Opinion final
Voilà!
Re: Question
Salut,
C'est une bonne idée, malheureusement la religion ne fera plus partie du programme de formation de l'école québécoise dès l'an prochain, ce n'est donc pas dans les plans.
Mais n'hésite pas à utiliser la zone d'entraide pour poser tes questions, nous y répondrons avec plaisir.
Karen
Re: Question
Salut!
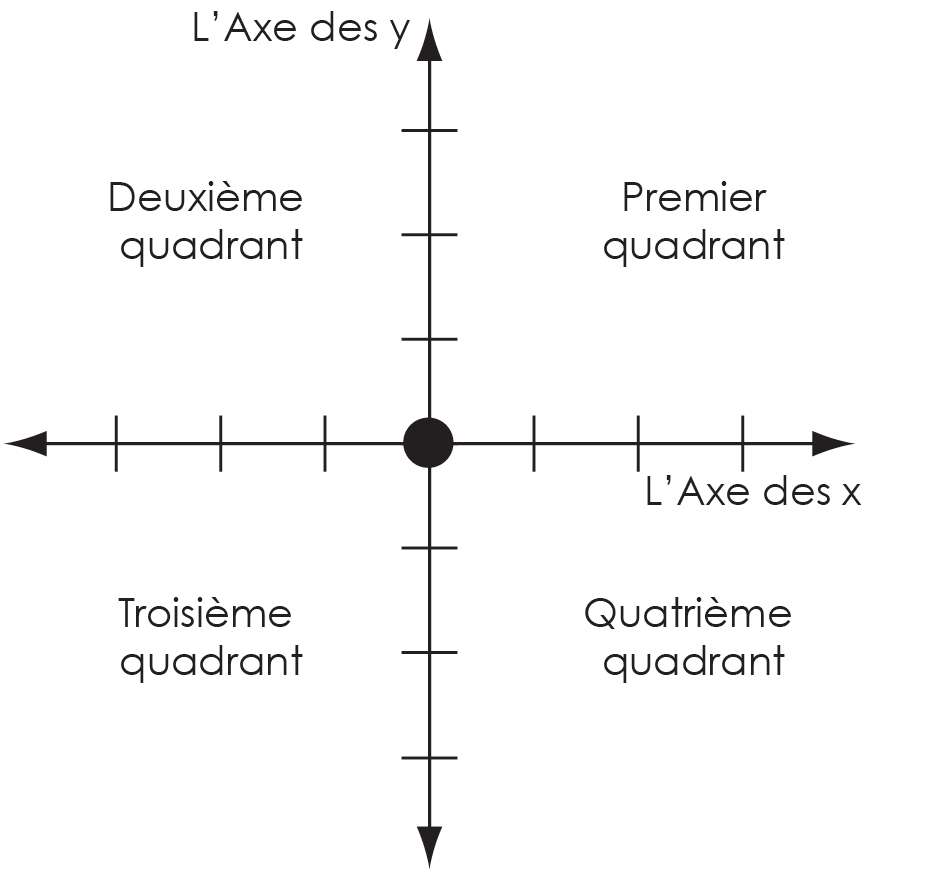
Dans un plan cartésien, les quadrants sont les quatre sections formées par l'axe des x et l'axe des y.
Le premier quadrant est celui en haut à droite, le deuxième est en haut à gauche, le troisième est en bas à gauche, et le quatrième est celui en bas à droite :
Voici une fiche qui pourrait t'être utile : Le plan cartésien | Secondaire | Alloprof
J'espère que c'est plus clair pour toi! :)
Question
Bonjour,
Si on me dit le point A est à l'origine du plan cartésien. Qu'est-ce que cela signifie ?
Merci !
BrachiosaureTimide314