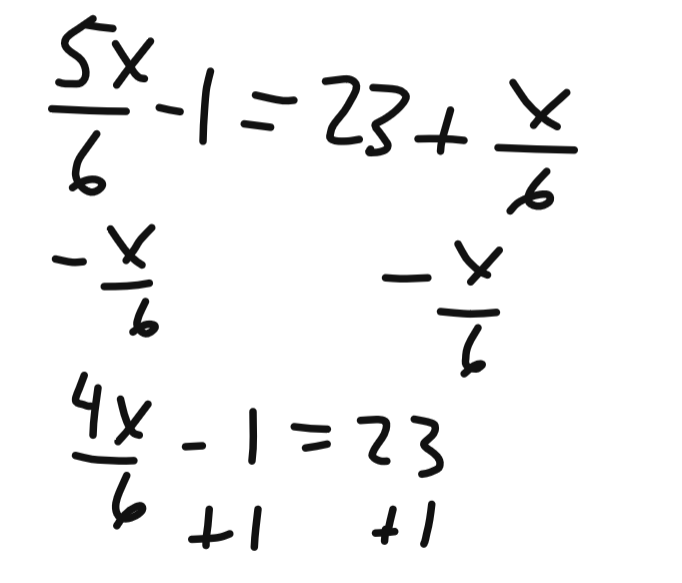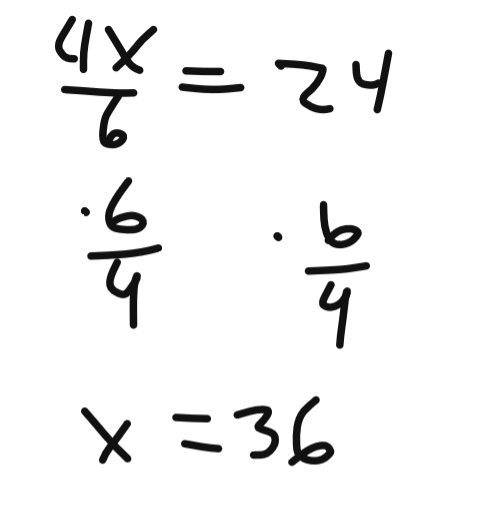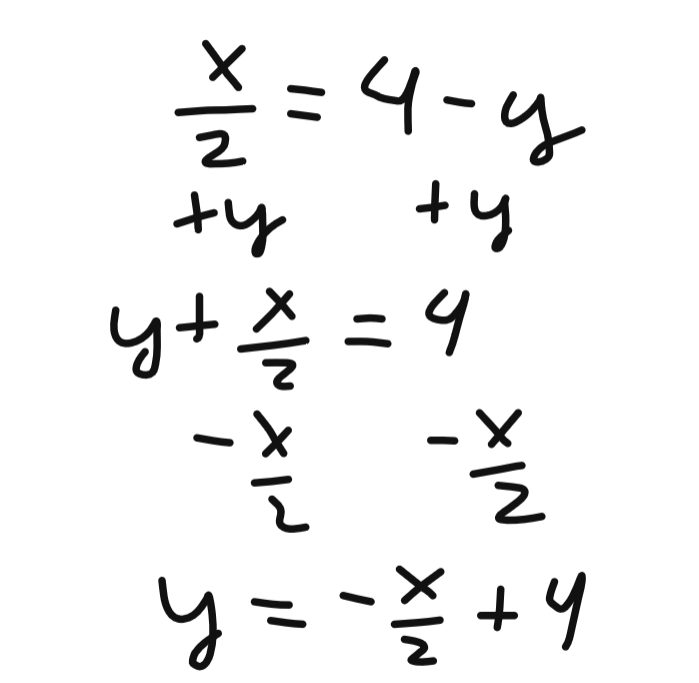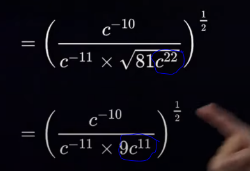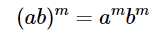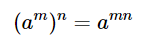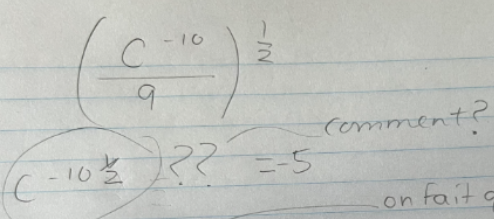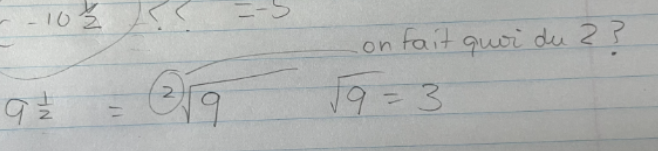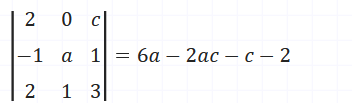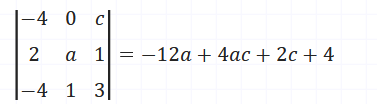Best Of

Bonjour, GomboCalme3167 !

Merci pour ta question d'aujourd'hui !

Pour y répondre, tu vas devoir calculer la fréquence \( \text{F} \) en te servant de la fréquence totale et de la mesure de l'angle donné au centre. En effet,

$$ \frac{\text{F}}{\text{F total}}=\frac{\text{angle}}{360} $$

Donc, $$ \frac{\text{F}}{100}=\frac{\text{angle}}{360} $$

Je te rappelle qu'il y a une relation entre la fréquence \( F \) et l'effectif comme suit:

$$ \frac{\text{Effectif}}{\text{Effectif total}}=\frac{F}{100} $$

Et une autre entre l'effectif et l'angle:

$$ \frac{\text{Effectif}}{\text{Effectif total}}=\frac{\text{angle}}{360} $$ 

https://www.alloprof.qc.ca/fr/eleves/bv/mathematiques/les-tableaux-en-statistique-m1364

Bons calculs !

N’hésite pas à nous recontacter si tu en as besoin. ;)

Salut PoivronOrange3912 😁

Merci pour ta question!

Tu as bien commencé.

Voici où ça a bloqué.

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

N'hésite pas si tu as d'autres questions 😊

À bientôt 😎

Salut!

Tu peux utiliser la méthode de substitution pour résoudre ce système d’équations, comme tu l’as fait au numéro a). Tu auras alors ceci : 

$$ \frac{x^2}{144} - \frac{(2x-40)^2}{81}=1$$

Tu peux ensuite développer (2x-40)², puis diviser la fraction en plusieurs petites fractions qui seront séparées par les signes d’addition ou de soustraction des termes au numérateur.

Je te laisse essayer avec ces indices. Si tu as d’autres questions, n’hésite pas à nous réécrire! :) 

Salut!

Ici :

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

La racine carrée peut se réécrire en exposant fractionnaire 1/2 grâce à cette loi des exposants :

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

On a donc :

$$ \sqrt{81c^{22}}$$

$$ (81c^{22})^{ \frac{1}{2} }$$

L'exposant se distribue sur chaque facteur :

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

$$ (81)^{\frac{1}{2}}(c^{22})^{\frac{1}{2}}$$

La racine carrée de 81 est 9 :

$$ 9(c^{22})^{\frac{1}{2}}$$

Puis, on peut multiplier les exposants 22 et 0,5 selon cette loi des exposants :

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Ce qui nous donne un exposant de 11, car \(22 \times \frac{1}{2}=11\):

$$ 9c^{11}$$

En ce qui concerne ta seconde question, tu dois appliquer les lois des exposants encore une fois.

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Ici, tu as l'exposant -10 × ½. Le résultat de cette multiplication est -5, donc :

$$ c^{-10 × \frac{1}{2}} = c^{-5}$$

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Une racine carrée peut s'écrire comme ceci \( \sqrt{}\) ou comme ceci \( \sqrt[2]{}\), c'est la même chose! ;) Il faut écrire l'indice lorsqu'il est différent de 2 seulement, donc lorsqu'on a une racine cubique, une racine quatrième, une racine cinquième, etc.

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Voilà! J'espère que c'est plus clair pour toi! :)

Salut!

Les nombres premiers sont des nombres divisibles que par 1 ou eux-même. Ex: 1, 3, 7 etc

Un nombre carré est un nombre qui est le résultat d'une multiplication de deux nombres pareils. Ex: 1x1=1, 2x2=4, 3x3=9, 4x4=16

La somme (le total) doit être inférieur ou égal à 25.

Salut WasabiComique8746😁

Merci pour ta question!

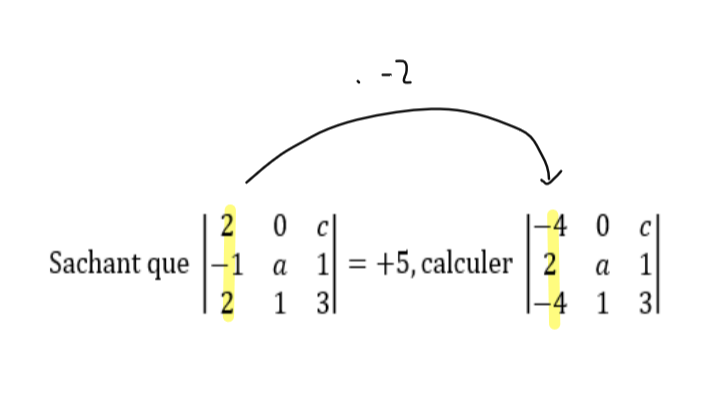
Les matrices!

Comme on peut le voir, ici, on multiplie par -2.

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Le déterminant de la première matrice est 6a - 2ac - c - 2 = 5.

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Le déterminant que la deuxième matrice est -12a + 4ac + 2c +4. On peut donc sortir le *-2, qu'on avait remarqué au début (avec une simple mise en évidence).

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

-2 (6a - 2ac - c - 2)

On peut substituer par 5 l'expression de départ, le déterminant de la première matrice.

On a alors -2*5= -10. Cela veut dire que le déterminant de la deuxième matrice est égal à -10.

N'hésite pas si tu as d'autres questions 😊

À bientôt 😎