Best Of
Re: Question
Salut ElfeHumble179!
Merci pour ta question. 🤩
Je ne crois pas que la personne gagnante soit annoncée au public.
Il est inscrit, dans les règlements du concours, que la personne gagnante "recevra un avis par courriel ou par téléphone dans les quarante-huit (48) heures ouvrables suivant le tirage, afin de lui annoncer qu'[elle] a gagné et de valider ses coordonnées".
On ne connait donc pas, ou pas encore, cette chanceuse personne!
En espérant que cela réponde à ta question. Si tu en as d'autres, n'hésite surtout pas à nous réécrire, il nous fera plaisir de t'aider à nouveau!
À bientôt,
Océane :)
Re: Question
Bonjour PerleChouette8861,
Merci pour ta question!
Est-ce que tu parles bien de la ligne du temps en histoire?
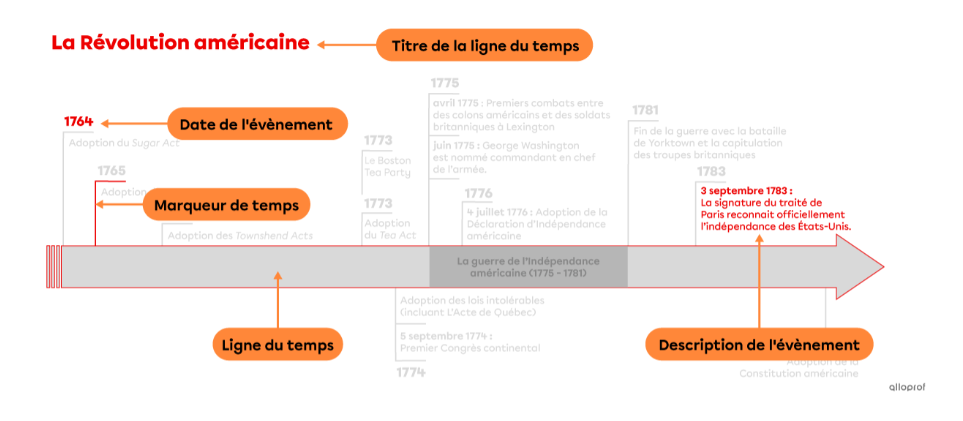
Si oui, la ligne du temps est une représentation de différents événements historiques, où ceux-ci sont situés en ordre chronologique sur une ligne.
Ainsi, en regardant la ligne du temps de gauche à droite, tu peux voir l'ordre d'arrivée des événements du plus ancien au plus récent.
Tu peux voir les différents éléments d'une ligne du temps sur l'image ci-dessous:
Je te laisse cette fiche en référence:
N'hésite pas à nous réécrire si tu as d'autres questions!
Re: Question
Bonjour, OrnithorynqueFormidable6152! :)
Merci pour ta question!
Tu ne dois pas être le seul qui a besoin d'éclaircissements à ce propos, puisqu'un autre jeune nous a déjà posé cette même question! Je t'invite à consulter la réponse en cliquant ici:
N'hésite pas à nous recontacter si des questions persistent. ✨
Iris
Re: Question
Salut GijuHabile4609!
Merci pour ta super question. 🤩
Dans cette phrase, j'aurais tendance à te dire que l'emploi de la virgule est grammaticalement correct, mais que celle-ci n'est pas indispensable à la phrase.
Pour plus d'informations à ce sujet, tu peux consulter cette fiche explicative :
En espérant que cela réponde à ta question. Si tu en as d'autres, n'hésite surtout pas à nous réécrire, il nous fera plaisir de t'aider à nouveau!
À bientôt,
Océane :)
Re: Question
Bonjour PlatineEnthousiaste7177,
Merci pour ta question!
Tu peux accéder à la messagerie lorsque tu es dans la Zone d'entraide, en cliquant sur la petite cloche en haut à droite de ton écran, juste à côté de ton identifiant. Elle ressemble à ça:
N'hésite pas à nous réécrire si tu as d'autres questions!
Re: Question
Salut DiplodocusKappa9249 !
Généralement, lorsqu'il est question de réaction, il faut s'attarder au nombre de mole. Donc, la première étape serait de convertir les masses en nombre de moles à l'aide de la masse molaire de chaque molécule.
$$ n=\dfrac{m}{M} $$
Puis, tu pourras calculer le rapport. J'espère que cela ait pu t'aider et si tu as d'autres questions, n'hésite pas !
Bonne soirée !
Question
Je voudrais m'assurer que:
1: la masse atomique représente les neutrons plus les protons ,
2: le numéro atomique représente le nbr de protons
3: si on fait la masse atomique moins le numéro atomique on aura le nombre de neutron.
Est ce que tout est vrai ou est ce qu'il y a des choses fausses ? Si oui veuillez s'il vous plait corriger ce qui est faux. Merci
Re: Question
Les autochtones deviennent de plus en plus dépendant des biens des Européens comme l'alcool, les armes les pots, etc.
Les Européens crée une nouvelle source de revenus avec la peau d'animal donc, vu que les autochtones apprécient les objets obtenus avec le troc des Européens, chaque clans autochtones vont à la chasse pour de la peau d'animal ce qui crée plus tard une baisse en population de viande et crée une crise.
Tous ça crée des guerres entre clans autochtones pour X, Y.
J'espère que ça t'aide!