Best Of

Salut!

On te donne la mesure du côté du carré en mètres, soit le nombre fractionnaire \(3\frac{1}{4}\).

Puisque l'aire d'un carré se calcule comme ceci :

$$ A=côté^2$$

Alors l'aire de ce carré est :

$$ A=(3\frac{1}{4})^2$$

$$ A=(3\frac{1}{4})\times (3\frac{1}{4})$$

Je te laisse faire le calcul. J'espère que c'est plus clair pour toi! :)

J'ai compris, merci Mme Katia et Mme Mélissa. J'ai aussi compris la dérivée et même son inverse, l'intégrale, j'ai fait mes recherches. La dérivée c'est genre le changement instantanée d'une fonction et l'intégrale est l'aire en dessous de la fonction.

Salut!

Oui, tes étapes sont bonnes, bien joué! :)

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Bonjour PommeAutonome7874,

Tes étapes semblent correctes, mais assure-toi de bien vérifier tes calculs. Il est important de bien comprendre comment calculer le prix unitaire et comment l'appliquer au total de mètres carrés pour obtenir le coût total. N'hésite pas à reprendre tes calculs pour t'assurer que tout est juste.

N'hésite pas à poser des questions!

Bonjour,

Si tu te réfères à mes explications dans ma précédente réponse : 

Le domaine commencerait à -10 et finirait à 3.

L'image serait plutôt de -7 à 6.

Le minimum serait -7 (le y du plus petit point).

Pourrais-tu m'expliquer ce que tu ne comprends pas exactement dans ces notions pour que je puisse mieux te les expliquer ?

Merci

Bonjour,

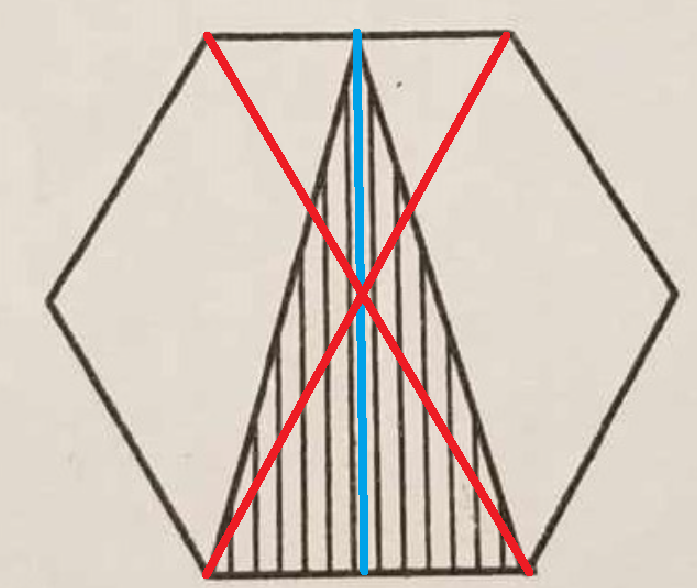
J'image que le problème pour toi c'est de trouvé l'aire de la partie hachurée.

Voici un indice:

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Comme tu peux le voir, la hauteur de ton triangle hachuré et égal à 2 fois la hauteur d'un triangle formant ton hexagone.

Bonne journée :)

N'hésite pas à venir nous voir si tu as encore besoin d'aide.

Bonjour,

L'aire latérale d'un solide est la somme des aires de toutes ses faces latérales, c'est-à-dire les faces qui ne sont pas une base du solide.

Par exemple, pour un prisme, l'aire latérale serait la somme des aires de tous les rectangles qui forment les côtés du prisme.

Pour un cylindre, l'aire latérale serait l'aire du rectangle qui est déroulé pour former le cylindre.

Pour calculer l'aire latérale d'un solide, tu dois trouver l'aire de chaque face latérale individuelle et les additionner.

Voici un lien utile :

N'hésite pas si tu as d'autres questions.

Bonne journée :)

Bonjour,

Ici nous voulons que tu remplisses ta table de valeur et une fois cela fait (pour le b) tu dois dessiner les points obtenus avec ta table de valeur sur ton graphique et relier ses points.

Pour trouver tes points il te suffit de remplacer la valeur de x donné dans ta formule pour trouve le y correspond.

ex : pour x = 10, et avec la formule y = 13.5x + 120, si on remplace x dans la formule :

y = 13.5x + 120 = 13.5 (10) + 120 = 135 + 120 = 155

Donc, on aura le point (10; 155)

Fais cela pour toutes les valeurs de x puis dessine les points obtenus sur ton graphique et relie-les

N'hésite pas si tu as d'autres questions.

Bonne journée

Salut PerleTurquoise1775!

🚗💨 Pour résoudre ce problème, tu peux utiliser la formule suivante: Temps = Distance / Vitesse. En remplaçant les valeurs données (70km pour la distance et 100km/h pour la vitesse), tu pourras trouver combien de temps l'automobiliste a roulé. Bon courage!👨‍🏫📝