Best Of
Re: Question
Bonjour DauphinFantastique379
Merci d'avoir utilisé la zone d'entraide alloprof pour répondre a tes questions
Tout d'abord, la phrase de exclamative sert à exprimer une émotion, un jugement ou un sentiment. Par la suite, la phrase impérative sert à exprimer un conseil, une demande ou un ordre. Finallement, la phrase déclarative permet de donner une information ou une opinion.
Voici une fiche qui pourrait t'aider:
https://www.alloprof.qc.ca/fr/eleves/bv/francais/les-types-de-phrases-f1134
J'espere que cela répond a tes questions
Ne lâche pas!
AzoteEfficace2134
Re: Question
Bonjour, DauphinFantastique379
Merci d'utiliser la zone d'entraide pour te venir en aide.
Concernant la question que tu as posée, une phrase exclamative démontre une émotion ou une réaction surprenante, avec de l'énergie ou de l'enthousiasme, une phrase impérative exprime un conseil, une demande ou un ordre. La phrase déclarative quant à elle, est une phrase ordinaire, qui n'exprime pas vraiment d'émotions ou d'ordre.
Si tu veux en apprendre plus sur le sujet tu peux consulter la fiche suivante :
https://www.alloprof.qc.ca/fr/eleves/bv/francais/la-phrase-de-base-et-ses-constituants-f1129
J'espère que cela répond à ta question.
Bonne étude,
CobraCharismatique5427
Re: Question
Bonsoir PerlePacifique6517,
Le meilleur moyen pour additionner facilement des fractions est de les mettre sur un dénominateur commun, puis d'additionner les numérateurs.
Pour mettre deux fractions sur un dénominateur commun, il faut trouver le PPCM. Voici une fiche pour savoir exactement comment y parvenir:
Ici, le ppm est 10. Pour la première fraction, comme le dénominateur est 5, on va devoir faire 5 x 2 pour arriver à 10. On fait la même opération pour le numérateur: 2 x 2 = 4. La première fraction est maintenant 4/10.
La deuxième fraction, étant déjà sur 10, nous n'y touchons pas.
Nous avons donc 2 fractions: 4/10 et 3/10. Pour les additionner, il faut simplement additionner les numérateurs (4 et 3) et mettre le résultat sur le dénominateur commun (10):
4+3=7 -» 7/10.
Si tu as d'autres questions, n'hésite surtout pas!
PotassiumLucide6364
Re: Question
Salut!
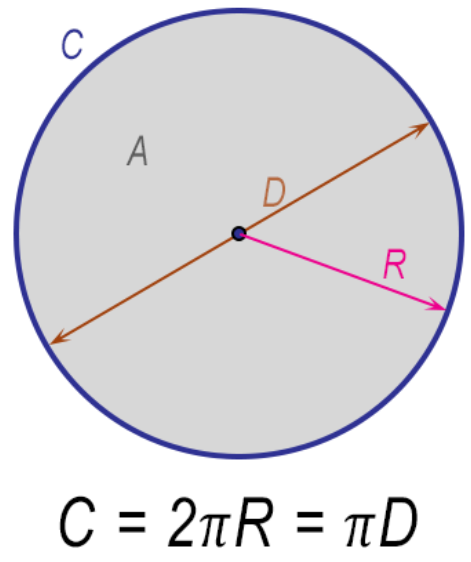
Tout d'abord, avec le diamètre, tu peux calculer la circonférence de la roue.
Si la circonférence est par exemple de 10 cm, cela signifie que la roue effectue 1 tour pour chaque 10 cm parcouru.
Ainsi, tu n'as qu'à diviser 100 000 cm (1 km) par la circonférence que tu auras trouvée pour déterminer le nombre de tours effectuées par la roue pour 1 kilomètre parcouru!
J'espère que c'est plus clair pour toi! N'hésite pas à nous réécrire si tu as d'autres questions! :)
Re: Question
Merci pour ta question!
En fait, indirectement le plateau élévateur du déodorant en bâton est un écrou. En effet, le mécanisme de vis et écrou ne nécessite pas que l'écrou soit immobile, ou que celui-ci soit reconnu comme étant un écrou officiellement. Ainsi, on peut considérer que l'écrou (le plateau élévateur) est immobile dans ce mécanisme et que la vis l'aide à se déplacer en étant immobile.
Cette fiche du site d'Alloprof explique les mécanismes de transformation du mouvement :
N'hésite pas si tu as d'autres questions!
Re: Question
Salut 😁
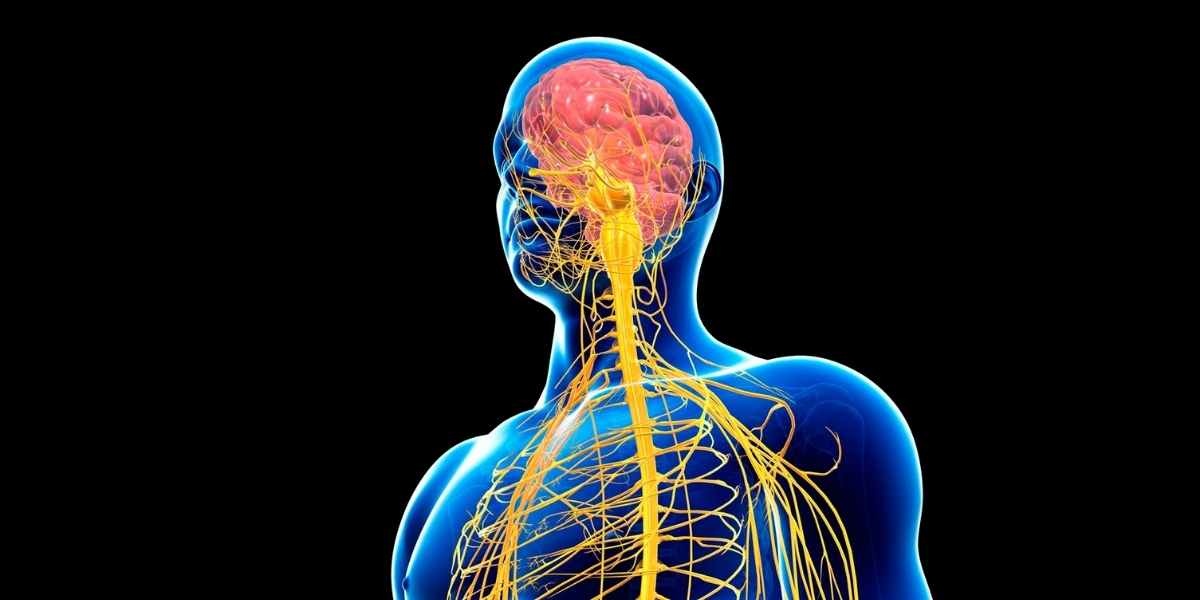
Le système nerveux est un peu comme des fils blancs qui se retrouvent dans le corps un peu partout, comme les branches d'un arbre.
La communication entre le cerveau et les nerfs (les fils blancs) permet de faire toute sorte de choses, comme ressentir la douleur, la douceur ou encore un picotement. 🥴
N'hésite pas si tu as d'autres questions 😊 À bientôt 😎
Re: Question
C'est la partie de ton cerveau qui fait que quand tu est en cours par exemple et que tu fais un examen tres important c'est sa qui va te rendre nerveux
Re: Question
Tu as très bien commencé.
Cependant tu as fait une erreur en déduisant le deuxième zéro de la toute petite parabole. Comme l'axe de symétrie est en x = 25 le deuxième zéro est (30,0)
Re: Question
Merci pour ta question!
Lors de l'acte volontaire, le parcours de l'influx nerveux est :
Cerveau → Nerfs moteurs → Muscles
OU, si le mouvement est plus bas que la tête Cerveau → Tronc cérébral → Moelle épinière → Nerfs moteurs → Muscles
Lors de l'acte involontaire, le parcours de l'influx nerveux est :
Nerfs sensitifs → Tronc cérébral → Nerfs moteurs
Lors d'un réflexe, le parcours de l'influx nerveux est :
Organes sensitifs → Nerfs sensitifs → Moelle épinière → Nerfs moteurs → Muscle
Cette fiche du site d'Alloprof explique précisément le parcours de l'influx nerveux dans ces trois situations :
N'hésite pas si tu as d'autres questions!
Re: Question
Bonjour!
Nous avons justement une fiche qui explique bien la multiplication! Elle contient même des vidéos que tu peux regarder pour mieux comprendre! :D
Voici le lien :
Si tu as d'autres question, n'hésite pas à nous réécrire. Nous te répondrons avec plaisir!
Laurie :)