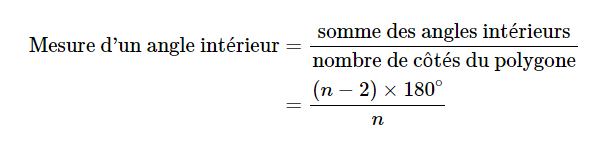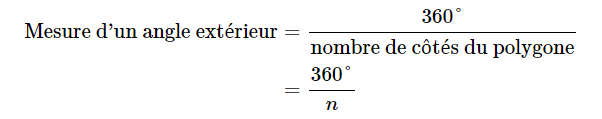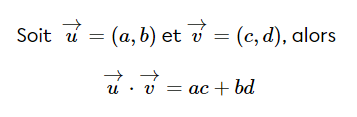Best Of
Re: Question
Bonjour ! :) Je vais tenter de mon mieux de répondre à tes questions.
- Puisque les usagers sont inscrits automatiquement au concours lorsqu'ils ou elles posent une question sur la Zone d'Entraide, il nous est impossible de prévoir le nombre de participant.es en avance. De ce fait, nous ne sommes pas en mesure de te donner un pourcentage ; cela dépend de l'achalandage de la ZE, qui varie selon plusieurs critères (si les élèves sont en périodes d'examens ou non, si les écoles ont fait la promotion des services Alloprof, si les écoles ont fait la promotion du concours, etc.)
- Alloprof est une organisation d'aide aux devoirs qui est en place depuis 1996. Elle est souvent mise de l'avant par les écoles et par le Ministère de l'Éducation, duquel nous recevons des subventions. :) Si tu souhaites en savoir plus sur l'organisation et te rassurer, tu peux chercher sur les web les nombreux articles de journaux à propos de notre plateforme. Le concours n'est donc pas une arnaque, je te rassure! :) C'est un bon réflexe par contre de se renseigner et de remettre en question ce que l'on voit sur Internet ☺. D'ailleurs pour participer au concours, tu n'as pas à payer quelque chose ni à entrer tes infos (avec cette question que tu viens de nous poser, tu es inscrit.e) ! :) Je t'invite à lire les règlements.
- Selon les règlements, non, ce ne sera que la première personne qui aura un prix (il n'y a qu'un.e gagnant.e). Par contre, comme tu peux le voir dans les règlements, si la personne ne réclame pas son prix, il y aura un autre nom tiré.
- Le gagnant ou la gagnante sera contacté.e en privé lorsque nous annoncerons le gagnant. Si il ou elle accepte le prix et accepte que l'on mette de l'avant ses informations (prénom et ville), une annonce sera sûrement faite sur notre page Facebook. C'est ce qui semble avoir été fait lors des dernières années. Tu peux voir ceci dans les règlements encore une fois. :)
- Tu pourrais féliciter la gagnante/le gagnant en faisant une publication sur la Zone d'Entraide, certainement :) C'est gentil de ta part !
Re: Question
Salut!
On ne te demande pas de trouver le volume de chaque solide, mais plutôt leur rayon. Pour cela, tu peux poser l'équation du volume total, soit :
$$ Volume_{total} = volume_{cylindre} + volume_{cône} $$
$$ 120\pi= volume_{cylindre} + volume_{cône} $$
Puis remplacer le volume du cylindre et celui du cône par leur formule de volume respective, soit :
Ce qui nous donne :
$$ 120\pi = A_{b}\times h_{cylindre}+ \frac{A_{b}\times h_{cône}}{3}$$
Puisque l'aire de la base est un cercle et que la formule d'aire d'un cercle est πr², nous avons alors :
$$ 120\pi= \pi r^2\times h_{cylindre}+ \frac{\pi r^2\times h_{cône}}{3}$$
Nous savons que la hauteur du cylindre est de 8 m et que celle du cône est de 16 m. Nous pouvons insérer ces données dans notre équation :
$$ 120\pi = \pi r^2\times 8+ \frac{\pi r^2\times 16}{3}$$
Il ne reste plus qu'à résoudre cette équation pour trouver la valeur de l'inconnu r, le rayon du solide.
Si tu le souhaites, tu peux ensuite calculer le volume du cône et celui du cylindre en utilisant le rayon que tu auras trouvé et les formules de volume de ces solides.
J'espère que c'est plus clair pour toi! Reviens nous voir si tu as d'autres questions! :)
Re: Question
Salut!
En anglais, le mot "renard" se dit "fox". Tu peux utiliser Google traduction pour traduire tous les mots que tu souhaites dans d'innombrables langues.
Si tu as d'autres questions, n'hésite pas à nous réécrire! :)
Re: Question
Salut!
Oui, le mot "banane" en anglais se dit "banana".
Reviens nous voir si tu as d'autres questions! :)
Question
Bonjour,
Comment résoudre cette équation?
Je ne sais pas quoi faire après.
Re: Question
Salut!
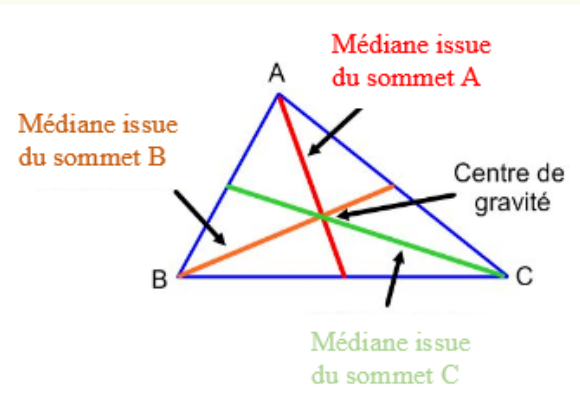
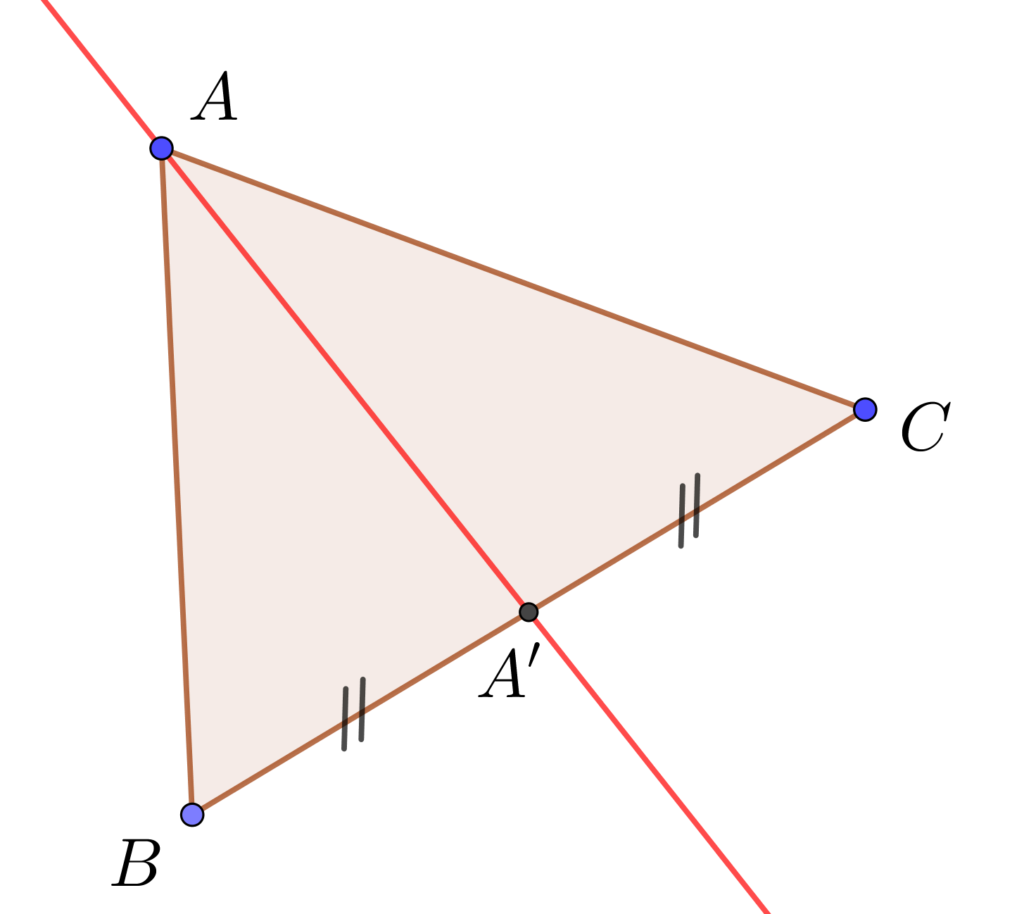
Une médiane est une droite reliant un sommet d'un triangle au point milieu du côté opposé.
Pour tracer une médiane à partir d'un sommet, tu dois mesurer le côté opposé, puis identifier le point milieu qui sépare en deux côtés égaux ce segment opposé. Par exemple, si le segment BC de la figure ci-dessous mesure 6 cm, alors le point milieu de ce segment sera à 3 cm de du sommet B et à 3 cm du sommet C. Ensuite, tu n'auras qu'à relier ce point milieu au sommet initial.
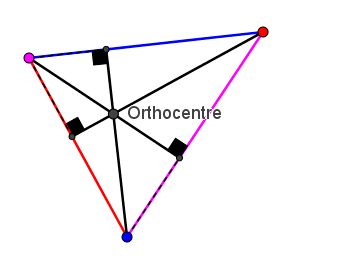
La hauteur est également un segment reliant un sommet à son côté opposé, mais formant un angle droit avec celui-ci, et n'étant pas nécessairement au milieu de ce côté opposé.
Ainsi, pour différencier une médiane d'une hauteur, tu dois vérifier si la droite coupe le côté opposé en deux segments égaux (médiane), et si ce n'est pas le cas, vérifier qu'un angle droit est formé avec le côté opposé (hauteur).
Je t'invite à consulter les fiches suivantes, elles expliquent la démarche à suivre pour tracer les différentes droites remarquables d'un triangle :
- La construction d'une médiane | Secondaire | Alloprof
- La construction d'une hauteur | Secondaire | Alloprof
Ainsi que cette fiche présentant une définition pour chacune de ces droites remarquables : Les droites remarquables | Secondaire | Alloprof
Concernant ta seconde question, tu peux utiliser la formule suivante pour trouver le nombre de côtés du polygone à partir de sa somme des angles intérieurs.
Pour trouver la mesure d'un angle intérieur et extérieur, tu as les formules suivantes :
J'espère que c'est plus clair pour toi! Reviens nous voir si tu as d'autres questions! :)
Re: Question
Salut!
Tout d'abord, le début de ta démarche est bon, bien joué! :)
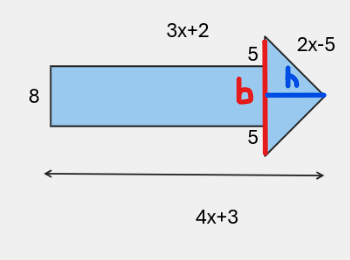
Tu as la bonne formule d'aire du triangle, soit \(A=\frac{bh}{2}\). Tu dois alors trouver la mesure de la base et de la hauteur. En d'autres mots, tu dois trouver ces mesures :
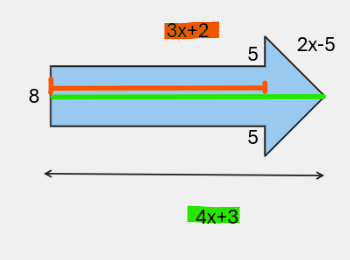
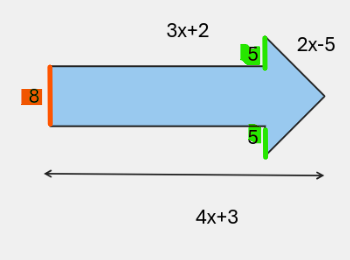
Pour trouver la hauteur du triangle, tu dois soustraire la mesure en orange suivante de la mesure en vert :
Pour trouver la base du triangle, tu dois additionner les mesures suivantes en vert et orange :
Une fois que tu connaitras la base et la hauteur, tu seras en mesure de calculer l'aire du triangle!
Si tu as d'autres questions, n'hésite pas à nous réécrire! :)
Question
Pourriez-vous m'aider, SVP ?
J'ai un oral à faire bientôt. Je ne suis pas très bonne en anglais, surtout à l'oral, donc il y a un fort probable que je pourrais échouer.
J'ai plusieurs problèmes :
— J'oublie tout ce que je veux dire quand tout le monde me regarde droit dans les yeux;
— Je stress tellement que j'ai des problèmes à parler normalement, donc cela me fait perdre des points ;
— Aussi, l'oral n'est pas avec un support visuel ! ! ! ! !
Svp, dites-moi qu'est ce que je dois faire!
Merci!
Re: Question
Bonjour ! :)
Il est normal d'être parfois stressé.e pour un oral. Heureusement, nous avons conçu plusieurs fiches avec de nombreux trucs pour préparer les exposés oraux!
Voici quelques conseils personnels :
- Pratique toi à la maison devant un miroir pour essayer de gérer ta gestuelle et tes expressions.
- Au lieu de regarder les autres élèves dans les yeux, balaye la classe des yeux ou regarde au fond de la classe (le mur).
- Essaie de te déplacer un peu en avant (marche doucement de gauche à droite, avance, recule, change ta posture). Cela va te faire paraître plus naturel et va aussi t'aider à évacuer ton stress.
- Rappelle-toi que c'est correct d'être stressé.e. Je sais que c'est difficile à faire et à te dire, mais cela ne veut pas dire que ton exposé est mauvais et cela ne veut surtout pas dire que les gens s'en rendent compte! :)
- Essaie de passer en premier (si tu veux). Comme ça, tu ne te compareras avec personne, tu auras moins de temps à stresser avant ton exposé et les enseignant.es sont souvent un peu plus indulgents ;) Dans tous les cas, cela te permettra de pouvoir profiter du reste de la période et d'écouter tes camarades. :D
Tu veux savoir un secret ? À chaque fois que je donne un premier cours, moi aussi je suis HYPER stressée ! Je tremble, j'ai la bouche pâteuse et j'ai l'impression que tout tourne à l'entour de moi. C'est normal :) Après quelques minutes ou quelques fois, on devient plus à l'aise.
Essaie de prétendre que tu expliques la matière à tes amis ou à ta famille. Ça risque de t'aider ! :D
Bon exposé ! :) Tu vas y arriver !
Sarah G
Re: Question
Salut!
Si la norme du vecteur U est 6, alors on a l'équation suivante :
$$ 6 = \sqrt{U_{x}^2+U_{y}^2}$$
où \(U_{x}\) et \(U_{y}\) sont les composantes du vecteur U.
De plus, le produit scalaire de deux vecteurs se calcule comme ceci :
Ainsi, si U•V est 13, alors on a l'équation :
$$ 13 =U_{x}V_{x} + U_{y}V_{y}$$
Puisqu'on connait les composantes \(V_{x}\) et \(V_{y}\) du vecteur V, soit (-8,3), alors on peut les insérer dans notre équation précédente pour avoir :
$$ 13 =-8U_{x}+ 3U_{y}$$
On a alors 2 équations et deux inconnus. Tu peux donc résoudre ce système d'équations pour trouver les composantes \(U_{x}\) et \(U_{y}\) du vecteur U.
Si tu as d'autres questions, n'hésite pas à nous réécrire! :)