Best Of
Re: Question
Bonjour!
Dans ce paragraphe, on explique que des personnes décident de devenir des religieux. Les religieux sont ceux qui s'occupent de l'éducation et des soins de santé des catholiques. Ils sont donc très importants! Imagine, sans les religieux de l'époque, ce serait comme ne pas avoir de médecins, d'infirmière et d'enseignants aujourd'hui!
J'espère t'avoir aidé à mieux comprendre! Si tu as d'autres questions, n'hésite pas à nous réécrire. Nous te répondrons avec plaisir!
Laurie :)
Question
Bonjour
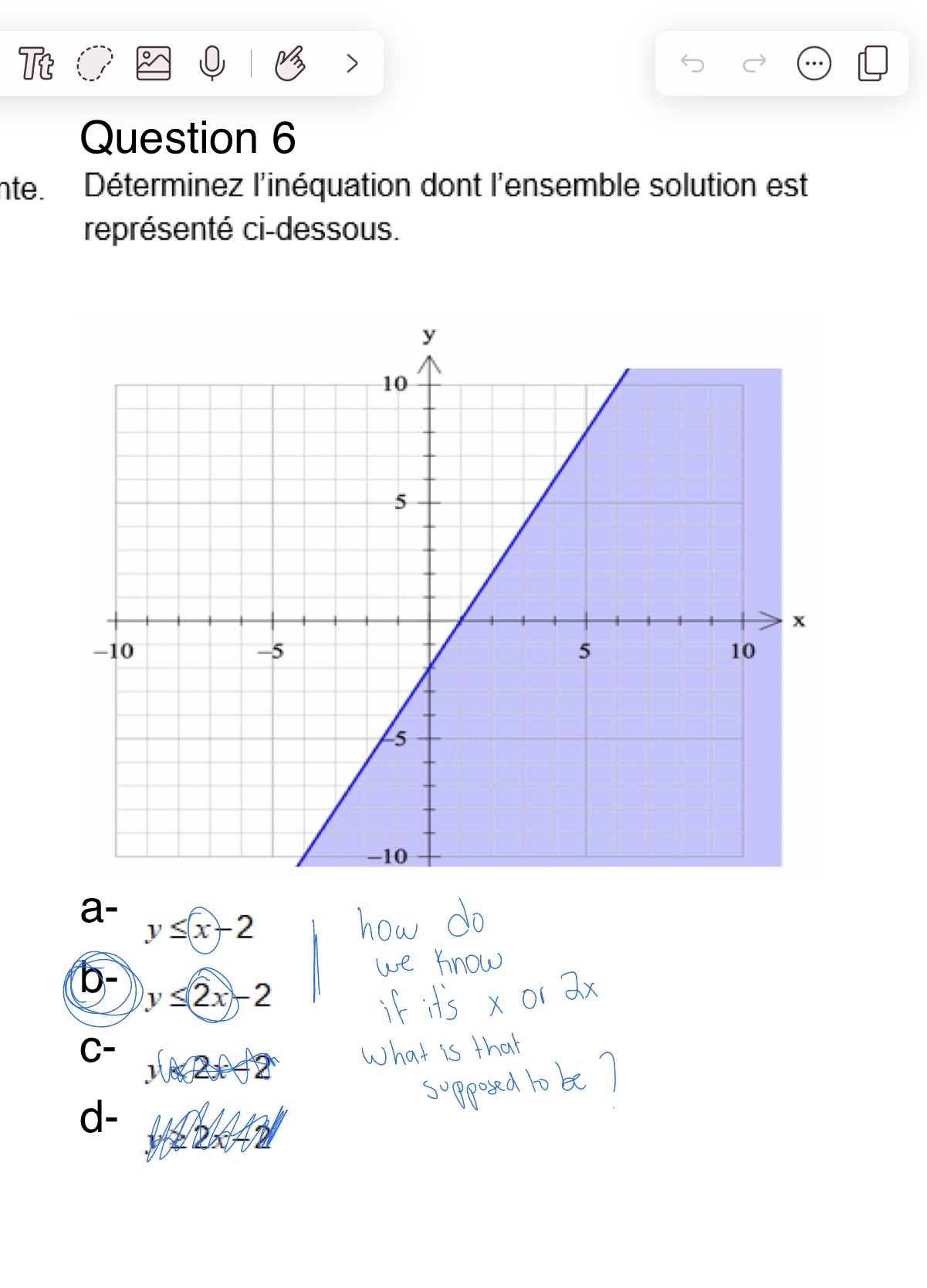
Ici je ne sais pas comment c’est 2x et pas x.
Comment dois je calculer pour trouver l’inéquation.
Question
Bonjour !
Demain, j'ai un examen d'histoire. Mais je ne comprends rien du tout ce paragraphe, pouvez-vous m'aider s.v.p ?
Merci et bonne soirée :D
Re: Question
Bonjour,
Tout dépend de quelle sorte de dessin tu parles mais si c'est un paysage commence par le derrière.
Pour le visage je ne sais pas comment te l'expliquer.Désolée
De rien
Question
Pourquoi la colonisation de saint Laurent était si lente dans 1608 à 1663
Question
Au déclenchement de la Guerre de la Conquête, qui a l'avantage, techniquement?
Re: Question
Bonjour!
Il est possible de transformer une subordonnée en groupe nominal en éliminant le subordonnant et en le remplacer par un nom. Voici un exemple avec une subornée complétive :
Justin espère qu'il gagnera la course.
Devient :
Justin espère gagner la course.
J'espère t'avoir aidé! Si tu as d'autres questions, n'hésite pas à nous réécrire. Nous te répondrons avec plaisir!
Laurie :)
Re: Question
Bonsoir, j'espère que tu vas bien :-)
Il est difficile de retracer l'origine officielle du Coran, puisque cela fait plusieurs années. Par contre, il aurait été écrit par Mahomet, mais ce n'est pas certain.
J'espère que cela répond à tes questions.
Bonne soirée!
Audrey
Re: Question
Bonsoir BB8Artistique2069
Tu aurais pu rechercher dans Google mais c'est pas grave. La capitale du Maroc c'est Rabat et si tu veut savoir il y a 1,959,388 habitants à Rabat.
DiamantHumoristique2503 ^v^
Re: Question
Salut LuneLogique1546,
Merci d'avoir utiliser la zone d'entraide d'Alloprof pour répondre à ta question.
Un segment est une partie de la droite.
Fait attention! Ce n'ai pas toute la droite, seulement une partie.
J'espère que cela t'aide.
Ne lâche pas!
WasabiSupra1286