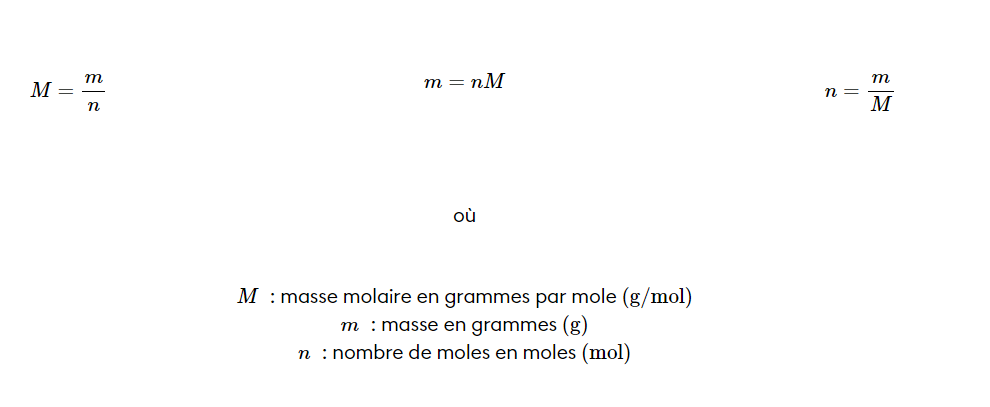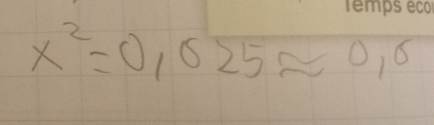Best Of
Re: Question
Bonsoir à vous !
Merci pour votre question. :)
En fait, dans ce problème, on souhaite ultimement savoir combien de fois l'aire d'un rectangle peut "entrer" dans l'aire de la grande surface.
Pour ce faire, il faut :
- Trouver l'aire totale de la grande surface. Celle-ci correspond à la mesure de la base multipliée par la mesure de la largeur. Il faut toutefois s'assurer que les deux mesures ont les mêmes unités !
- Trouver l'aire d'un rectangle. Celle-ci correspond à la mesure de la base multipliée par la mesure de la largeur.
- Diviser la mesure d'aire de la grande surface par la mesure d'aire d'un rectangle. Il faut toutefois s'assurer que les deux mesures ont les mêmes unités !
- Si la réponse de cette division est un nombre entier (sans virgule), cela signifie qu'il n'est pas nécessaire de couper de rectangle pour recouvrir la surface. La réponse indique ainsi le nombre de rectangles nécessaires pour recouvrir entièrement la surface.
- Si la réponse est un nombre décimal (avec virgule), cela signifie qu'il faudra couper un rectangle pour recouvrir entièrement la surface.
En espérant que cela éclairera votre fille ! N'hésitez surtout pas à nous réécrire si vous avez d'autres questions !
Océane :)
Re: Question
Merci pour ta question!
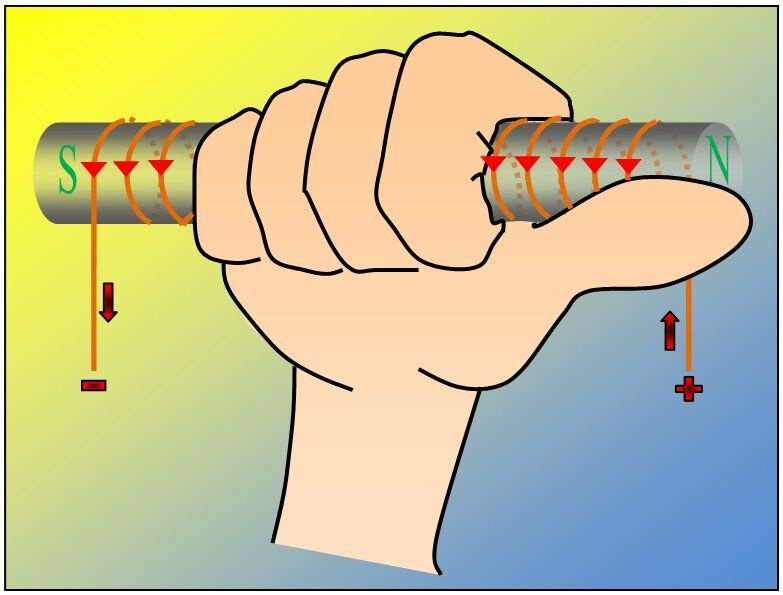
Tu peux utiliser la règle de la main droite. Selon cette règle, le pouce de la main droite pointe le pôle nord et la direction des doigts pointe le sense du courant.
Ainsi, tu n'as qu'à positionner ton pouce droit pour pointer le nord et ainsi déterminer la direction du courant.
Cette fiche du site d'Alloprof explique la règle de la main droite :
N'hésite pas si tu as d'autres questions!
Re: Question
Τu as besoin de te rappeler que
l'aire totale d'un cylindre = aire de deux bases + aire latérale
aire latérale d'un cylindre = 2π·rayon·hauteur
aire de la base d'un cylindre = π·rayon²
Re: Question
Salut!
Tu dois utiliser l'équation suivante pour trouver le nombre de moles :
comme ceci :
$$ n = \frac{5}{M_{H_{2}O}}$$
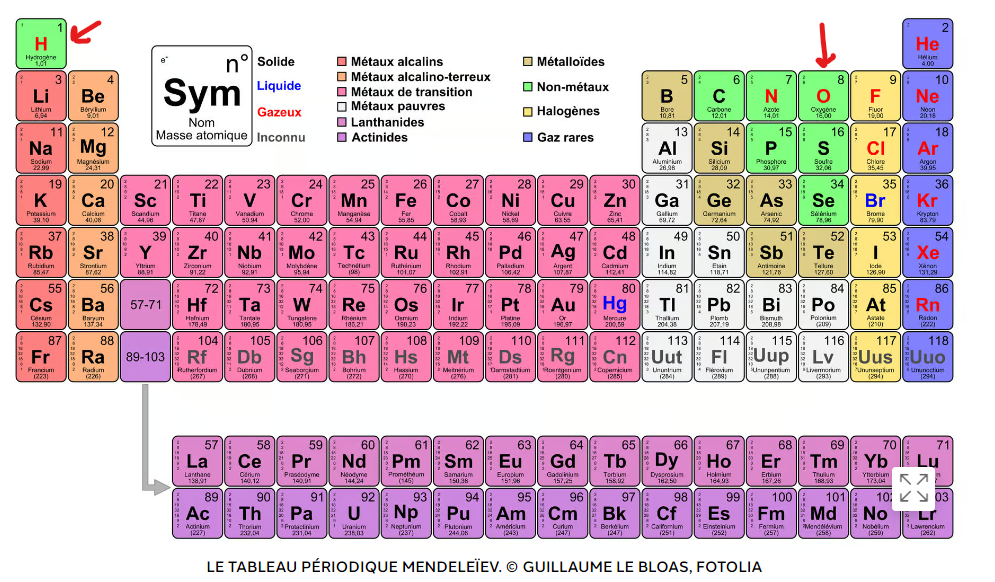
Pour trouver la masse molaire de l'eau, donc de \(H_{2}O\), tu dois te servir de ton tableau périodique :
$$ M_{H_{2}O} = 2\times M_{H} + M_{O}$$
$$ M_{H_{2}O} = 2\times 1,01 + 16=18,02 ~g/mol$$
Nous pouvons alors trouver le nombre de moles d'eau :
$$ n = \frac{5}{18,02}=0,27747~mol$$
Un mole d'eau contient \(6,022 \times 10^{23}\) molécules d'eau (nombre d'Avogadro). Ainsi, 0,27747 mole d'eau contient :
$$0,27747~ mol \times 6,022 \times 10^{23} ~particules/mol = 1,67 \times 10^{23} ~particules$$
Il y a donc \(1,67 \times 10^{23}\) molécules de \(H_{2}O\) dans 5 g d'eau. Puisque chaque molécule de \(H_{2}O\) possède 2 atomes d'hydrogène, alors il y a \(1,67 \times 10^{23} \times 2 =3,34 \times 10^{23}\) atomes d'hydrogène dans 5 g d'eau.
Voici des fiches sur ces notions qui pourraient t'être utiles :
J'espère que c'est plus clair pour toi! :)
Re: Question
Salut ThonSigma563 !
Merci pour ta question. :)
Ce groupe de mot est un groupe prépositionnel. Effectivement, son noyau est la préposition "dans" et sa fonction est complément de phrase.
Pour en apprendre davantage sur le groupe prépositionnel, je t'invite à consulter cette fiche !
N'hésite surtout pas à nous réécrire si tu as d'autres questions !
Océane :)
Re: Question
Salut NeptuneTenace1734 !
Merci pour ta question. :)
Je te réfère à cette fiche explicative qui contient tous nos meilleurs trucs pour étudier en histoire ! Tu y trouveras définitivement une méthode efficace qui te permettra d'être prêt.e pour mercredi !
N'hésite surtout pas à nous réécrire si tu as d'autres questions et bon succès dans ton examen !
Océane :)
Re: Question
Bonjour JupiterAimable,
Merci pour ta question!
Je n'ai malheureusement pas de résumé de cahier de sciences à te proposer. Cependant, Alloprof propose des vidéos sur les lois de Kirchhoff:
Ainsi qu'une fiche explicative sur la loi d'Ohm:
Voici aussi un répertoire de révision sur toute la matière couverte en sciences de secondaire 4!
STE:
ST:
N'hésite pas si tu as encore besoin d'aide:)
Kylan
Re: Question
Bonsoir JupiterAimable5315!
En plus des suggestions qui t'ont été données, je te suggère de consulter le répertoire de révision de ST de 4e secondaire. Tu pourras y trouver tous les sujets couvert par le programme ainsi les exercices et les vidéos que tu peux consulter. Tu as l'embarras du choix. Voici le lien pour y arriver:
Bon succès pour la réussite de ton cours!
N'hésite pas à nous écrire si tu as d'autres questions!
ThonLucide8631
Re: Question
Salut!
Ta démarche est excellente au numéro a), tu as seulement oublié de faire la racine carrée de 0,625 pour avoir la valeur de x.
$$ x^2 = 0,625$$
$$ \sqrt{x^2} = \sqrt{0,625}$$
$$ x ≈0,79$$
Pour le b), tu dois calculer f(0,4), c'est-à-dire la valeur de y lorsque x=0,4.
Si tu as d'autres questions, n'hésite pas à nous réécrire! :)
Re: Question
Salut!
Tout d'abord, tu dois trouver l'équation de la fonction exponentielle de Julien ainsi que celle de Juliette.
Pour Juliette, on nous dit que le montant initial est de 1000$ et que le taux d'intérêt composé annuel est de 10%. Nous pouvons traduire cela en l'équation ci-dessous :
$$C_{n~Juliette}=1000(1+0,10)^n$$
$$C_{n~Juliette}=1000(1,1)^n$$
Pour Julien, on sait que le montant initial est de 1000$ et que le taux d'intérêt composé annuel est de 8 %. Nous avons alors l'équation suivante :
$$C_{n~Julien}=1000(1+0,08)^n$$
$$C_{n~Julien}=1000(1,08)^n$$
Cependant, puisque Juliette fait son placement un an après Julien, nous allons alors calculer le montant que possède Julien un an après le début de son placement afin que la variable n soit le nombre d'années écoulées depuis le placement de Juliette.
$$C_{n~Julien}=1000(1,08)^1$$
$$C_{n~Julien}=1000(1,08)$$
$$C_{n~Julien}=1080$$
Julien possède donc 1080$ au moment où Juliette fait son placement. Nous allons poser cela comme notre valeur initiale. L'équation de Julien devient alors :
$$C_{n~Julien}=1080(1,08)^n$$
Par exemple, si Julien a fait son placement en 2020 et Juliette en 2021, la variable n représente le nombre d'années écoulées depuis 2021. Puisque Julien possède 1080$ en 2021, alors ce montant sera notre valeur initiale.
Si nous n'avions pas changé le montant initial (si nous avions gardé le 1000$ comme montant initial), alors la variable n pour l'équation de Julien serait le nombre d'années écoulées depuis 2020 et la variable n pour l'équation de Juliette serait le nombre d'années écoulées depuis 2021, ce qui ne nous permet pas de faire les prochains calculs!
Ensuite, on veut trouver le nombre d'années écoulées lorsque le capital accumulé sera le même pour les deux amis. En d'autres mots, on cherche la valeur de la variable \(n\) lorsque \(C_{n~Julien}=C_{n~Juliette}\). Tu dois donc résoudre cette équation :
$$1080(1,08)^n=1000(1,1)^n$$
Voici le début de la résolution :
$$\frac{1080}{1000}(1,08)^n=(1,1)^n$$
$$1,08(1,08)^n=(1,1)^n$$
En appliquant les lois des exposants, nous avons :
$$(1,08)^{n+1}=(1,1)^n$$
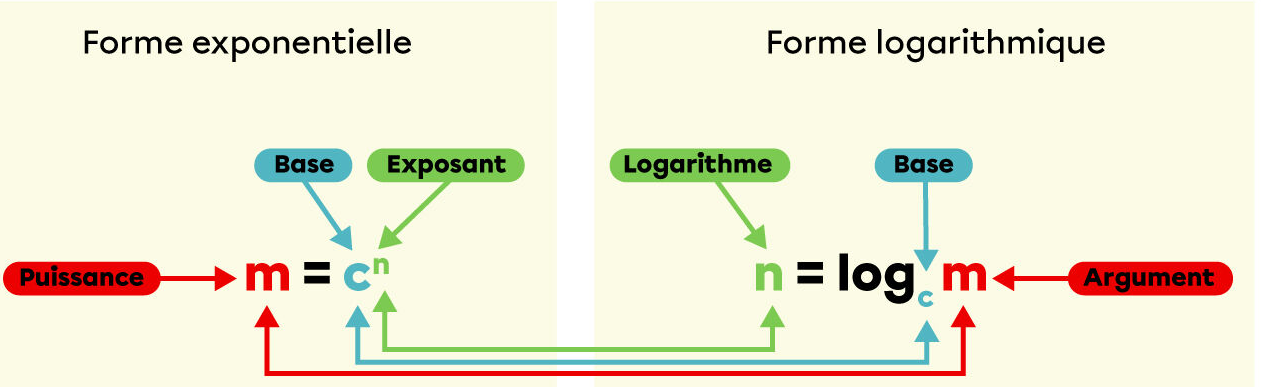
Tu dois ensuite transformer la forme exponentielle en forme logarithmique.
Je te laisse continuer. N'oublie pas d'additionner 1 à la valeur de n que tu auras trouvée, puisqu'on te demande de trouver le nombre d'années écoulées depuis le placement de Julien, alors que notre variable n représente le nombre d'années écoulées depuis le placement de Juliette!
Voici des fiches sur ces notions qui pourraient t'être utiles :
- Le taux d'intérêt composé | Secondaire | Alloprof
- La résolution de problèmes impliquant la fonction exponentielle | Secondaire | Alloprof
- Les logarithmes | Secondaire | Alloprof
J'espère que c'est plus clair pour toi! :)