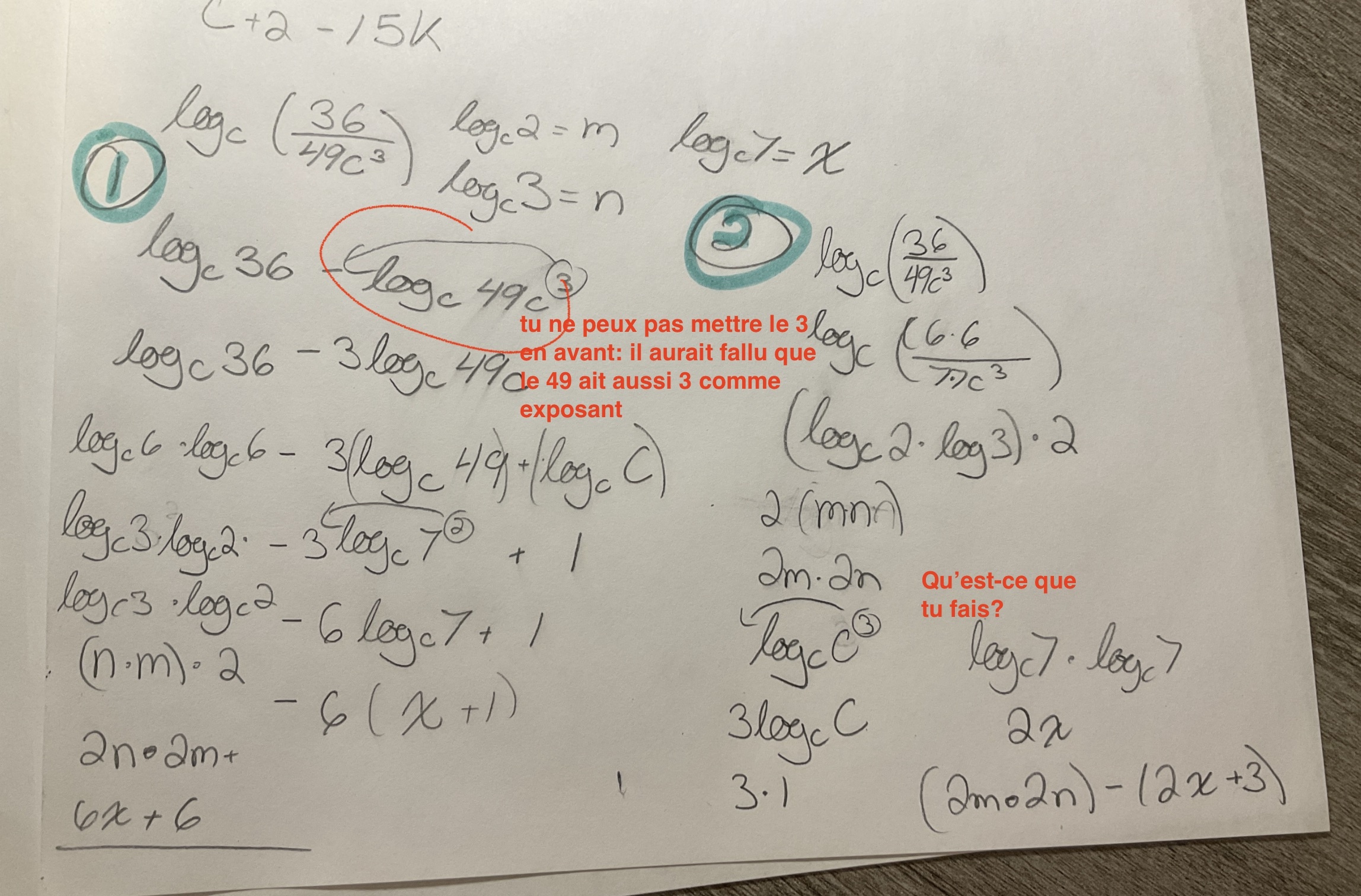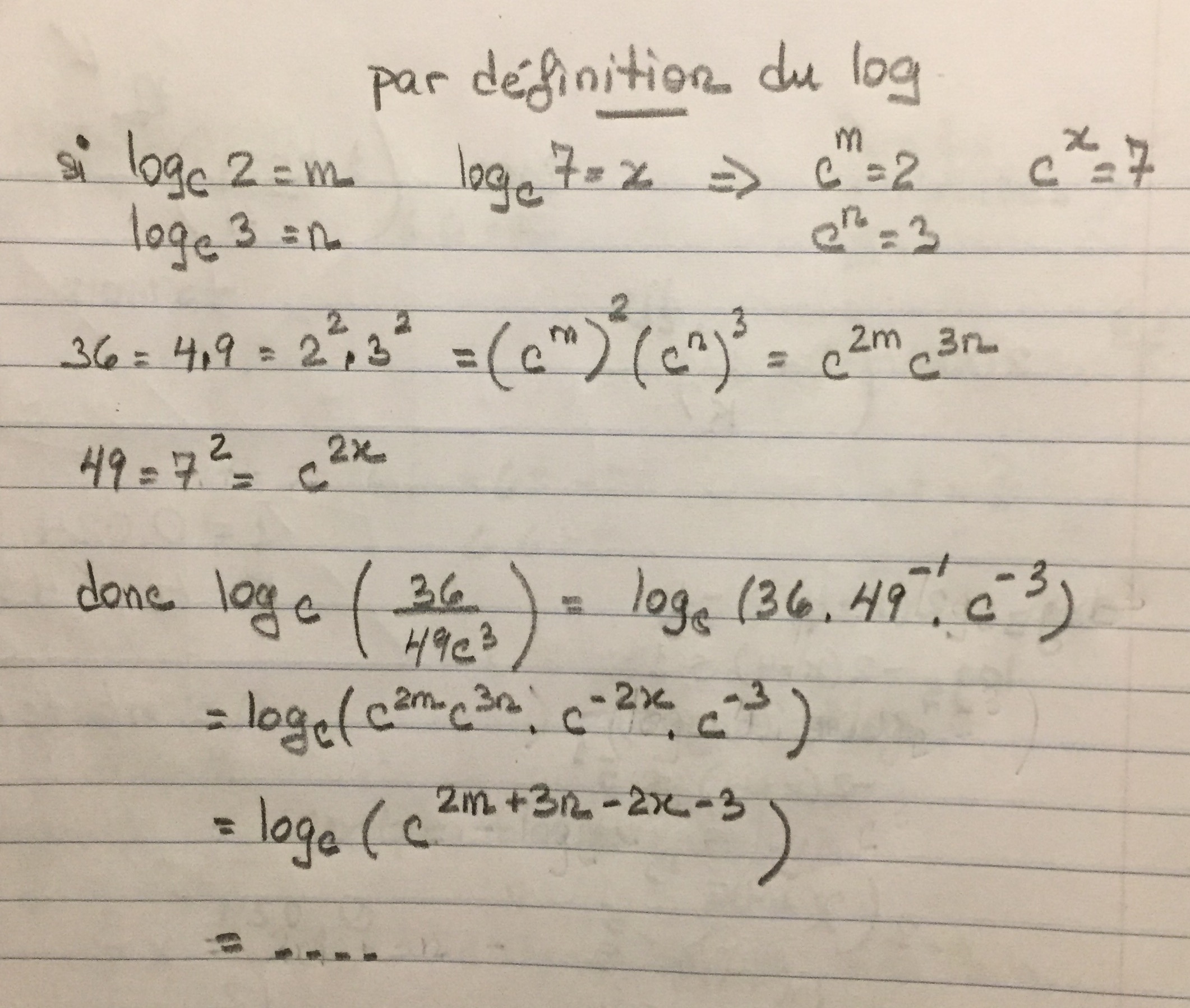Best Of
Re: Question
Bonsoir ! :)
Plusieurs élèves ont de la difficulté à apprendre leurs tables par cœur. C'est pourquoi nous avons conçu cette fiche qui te donne plusieurs trucs pour apprendre tes tables : https://www.alloprof.qc.ca/fr/eleves/bv/mathematiques/trucs-pour-apprendre-les-tables-par-coeur-m1423.
Tu peux aussi te pratiquer tout en t'amusant en jouant à nos deux jeux :
https://www.alloprof.qc.ca/fr/eleves/bv/jeux/meteormath-2
Tu es capable ! :D
Sarah G
Re: Question
Bonsoir, ArgentTranquille7674,
Merci de solliciter nos services.
Afin de tout connaitre concernant l’aire et le périmètre, je t’invite à cliquer sur les liens ci-dessous.
N’hésite pas à nous réécrire si tu as d’autres questions!
Émilie
Re: Question
Bonsoir, AluminumMirifique8596,
Merci de solliciter nos services.
Tes calculs me semblent être justes et adéquats.
Bonne continuité!
Émilie
Re: Question
Bonsoir, ParulineRose3048,
Merci de solliciter nos services.
Malheureusement, les membres de l’équipe d’Alloprof n’ont pas comme mandat de corriger les productions écrites des élèves.
Cependant, je peux te dire que ton texte est très bien écrit. Je t’invite à revoir la dernière phrase de ton deuxième paragraphe puisque je crois que tu devrais retravailler le sens de ta phrase afin qu’elle soit plus claire.
Continue ton bon travail et n’hésite pas à nous réécrire si tu as d’autres questions!
Émilie
Question
Dans un texte, il y a des thèmes. Comment faire pour bien le justifier?
Re: Question
Tu ne devrais pas garder toute ton étude pour le lendemain mais tu devrais étudier les trucs que tu as le plus de mal pour avoir une chance de passer ton examen
Bonne chance !!!
Re: Question
Salut LuneLibre3627!
Merci d'avoir utilisé la zone d'entraide pour répondre à tes questions.
D'abord, je te conseille de ne pas tout laisser à la dernière minute. Divise plutôt tes notions dans la semaine (par exemple faire 15 minutes d'exercices de mathématiques chaque jour est plus efficace que de faire 3 heures la veille).
Néanmoins, je t'invite à consulter la fiche ci-dessous qui t'offre des astuces pour rendre tes révisions plus efficaces:
Nous sommes toujours là pour t'aider!
Bon examen :)
PoivronRouge571
Re: Question
Bonjour TyrannosaurePhilosophe,
Merci de faire appel à nos services! :)
Pour connaitre les différents changements d'état, je te conseille de lire cette fiche :
Tu y trouveras des informations complètes sur les six changements d'état ainsi que des exemples.
Pour bien les retenir, je te suggère de refaire le schéma de changements de phases. Également, tu peux te faire une feuille de notes complètes qui résume la matière ou tu peux te faire des cartons de révision.
N'hésite pas à nous réécrire si tu as d'autres questions! :)
Marilee
Re: Question
A moins que j'ai mal interprété tes calculs, je dirais que ni l'une ni l'autre est bonne.
Une manière plus simple il me semble:
Note: on peut procéder de différentes façons en autant qu'on respecte les lois des logarithmes