Best Of
Question
Bonjour, auriez-vous des exercices pour pratiquer la différence entre la réflexion spéculaire et diffuse ? Merci beaucoup.
Re: Question
Salut, LithiumSigma6463! :)
Merci pour ta question.
Non, le compte rendu n'est pas comme un texte narratif. Ils portent tous les deux des rôles et des objectifs différents.
Un compte rendu rend compte de faits réels, d'une réunion, d'un événement, d'un livre (compte rendu de lecture) de manière objective et neutre.
Un texte narratif raconte plus une histoire racontée par un narrateur. Il s'agit d'un texte qui décrit une succession de faits qui s'enchaînent. Il présente un ou des personnages qui évolue(nt) dans un temps donné et un lieu donné.
Lors de la rédaction d'un compte rendu, il vaut mieux élaborer un texte fluide, continu, seulement interrompu par d’éventuels intertitres si le confort du lecteur le demande. Le style question/réponse est, en principe, à éviter. Le découpage en paragraphes se détermine en fonction des thèmes sélectionnés durant la précédente phase de préparation.
Voici notre fiche sur le compte rendu:
N'hésite pas à nous réécrire si tu as d'autres questions!
Iris
Re: Question
Salut AiglePacifique4611!
Voici la réponse à ta question.
La majorité de la production hydroélectrique du Québec se fait dans la Baie-James en raison de la capacité de production immense de ce complexe, de sa flexibilité pour équilibrer le réseau électrique, et de la décision de développer les ressources du nord suite au rejet des projets dans le sud. De plus, la construction de ce grand chantier a permis à Hydro-Québec de se développer et a fourni à la province une source d'énergie abondante et peu coûteuse.
J'èspère que ça t'aide! ;3
Emma.
Re: Question
Salut!
Tu peux multiplier des grands nombres en les plaçant l'un en dessous de l'autre, puis en multipliant le premier chiffre du nombre en bas par chaque chiffre du nombre en haut.
Voici un exemple :
Je t'invite à consulter cette fiche pour plus de détails : Multiplier des nombres | Primaire | Primaire | Alloprof
Si tu as d'autres questions, n'hésite pas à nous réécrire! :)
Re: Question
Salut!
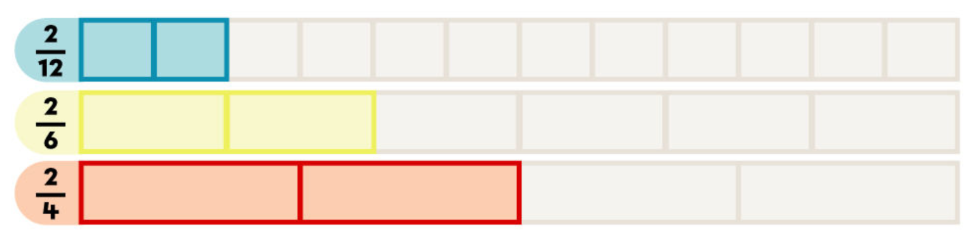
Lorsque les fractions ont toutes le même numérateur, ce sont les dénominateurs qui vont nous permettre de déterminer si une fraction est plus petite ou plus grande qu’une autre.
Par exemple, préfèrerais-tu manger 2 pointes d'une pizza coupée en 12 pointes équivalentes (2/12), ou 2 pointes d'une pizza coupée en 4 (2/4)? Si on a très faim, alors on choisira assurément la seconde option, puisque nos deux pointes seront beaucoup plus grosses!
Donc, lorsque les numérateurs sont identiques, plus le dénominateur est grand, plus la fraction est petite.
Si les dénominateurs ne sont pas pareils, alors tu dois transformer les fractions en des fractions équivalentes pour qu'elles aient toutes le même dénominateur. Tu pourras ensuite comparer les fractions en comparant les numérateurs. En résumé, pour ordonner des fractions ayant des dénominateurs différents, tu dois suivre ces étapes :
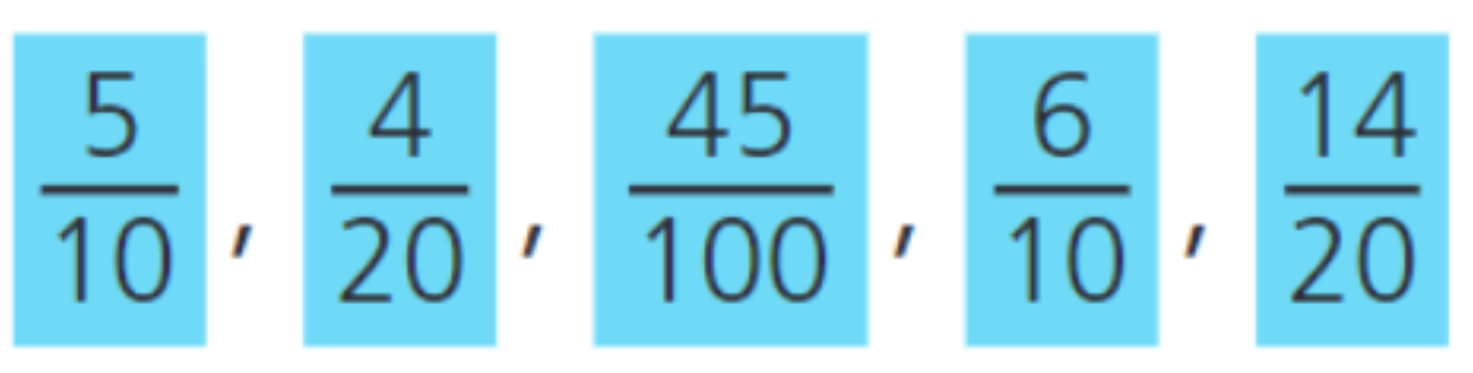
Par exemple, si nous voulons ordonner ces fractions :
On doit transformer les fractions afin que leur dénominateur devienne 100. Voici un exemple :
$$ \frac{4}{20} = \frac{?}{100}$$
Pour trouver le numérateur de la fraction équivalente, on se pose la question suivante : par quoi on multiplie 20 pour avoir 100? La réponse est 5. Ainsi, puisqu'on a multiplié le dénominateur 20 par 5, alors on doit aussi multiplier le numérateur par 5 :
$$ \frac{4\times 5}{20\times 5} = \frac{20}{100}$$
Nous avons ainsi transformé 4/20 en une fraction équivalente dont le dénominateur est 100. Tu dois faire cela pour toutes les fractions dont le dénominateur n'est pas déjà 100. Puis, tu pourras ordonner les fractions initiales.
Voici une fiche sur cette notion qui présente plusieurs exemples similaires : Ordonner des fractions et des nombres fractionnaires | Secondaire | Alloprof
J'espère que c'est plus clair pour toi! N'hésite pas si tu as d'autres questions :)
Re: Question
Salut!
C'est une bonne question! :)
« Postsecondaire » désigne ce qui se situe après les études secondaires. Lorsque tu vois un élève sur la zone qui a un niveau « post secondaire», cela veut dire que cet élève a, généralement, terminé ses études secondaires.
Le postsecondaire inclut divers établissements d'études supérieures comme les cégeps, les universités ainsi que les centres de formations professionnelles.
N'hésite pas à nous réécrire si tu as d'autres questions! :)
Re: Question
Salut CoccinelleRomantique2641!
Merci pour ta question. 🤩
Tu n'es pas la seule personne qui se questionne sur le sujet! Je t'invite donc à consulter la super explication qui a été donnée à cette question semblable à la tienne. 😄
En espérant que cela réponde à ta question. Si tu en as d'autres, n'hésite surtout pas à nous réécrire, il nous fera plaisir de t'aider à nouveau!
À bientôt,
Océane 💫
Re: Question
Bonjour Coucoumignon
Je comprends que cette erreur peut être difficile à trouver, car, en français, on dit "Ne regarde pas mon devoir, c'est tricher". Or en anglais, on écrit le verbe "regarder" (look) comme ceci :
Looking at something. (regarder à quelque chose)
Donc, dans ta phrase, tu as utilisé le verbe selon sa forme en français.
Exemple:
Forme fautive: I look my phone.
Forme correcte: I look at my phone.
J'espère avoir pu t'aider! Si tu as d'autres questions, n'hésite pas à nous réécrire!
Re: Question
Salut!
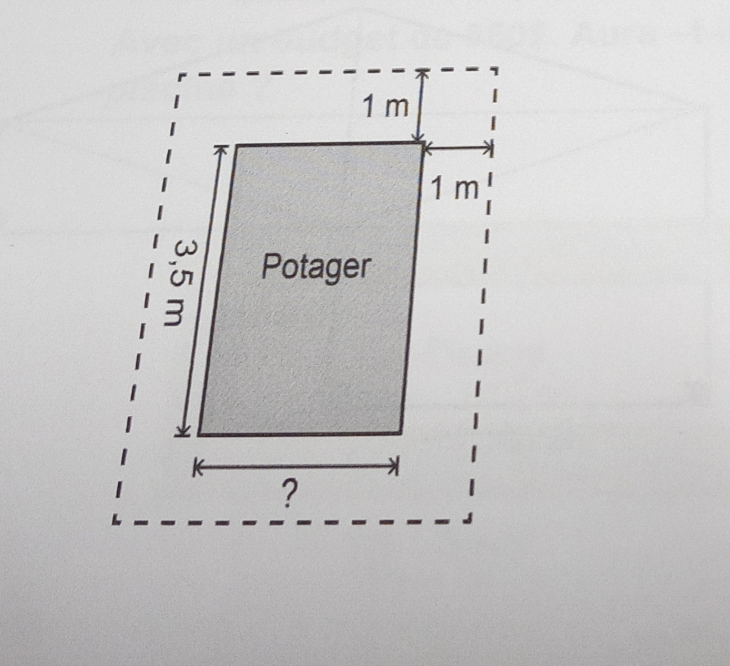
On te dit que 7,62 m = 23,99$. Tu peux imaginer qu'en magasin, les paquets de grillage se vendent à 7,62 m chacun.
On sait qu'on a payé 76,06$. Donc, si tu divises ce montant par 23,99$, tu peux trouver le nombre de paquets de 7,62 m achetés.
Ensuite, tu multiplies ce nombre de paquets par 7,62 m pour avoir la longueur totale de grillage acheté, et tu y soustrais 3,86 m (les restants) pour déterminer la longueur de grillage posée.
Tu auras alors le périmètre du rectangle en pointillé :
Je te laisse continuer avec ces indices. Si tu as d'autres questions, on est là! :)
Re: Question
Salut LoupAlpha4750!
Merci pour ta question. 🤩
À ma connaissance, il n'y a pas d'endroit où tu peux consulter les explications que tu as publiées.
Par contre, la prochaine fois que tu publies une explication, tu peux te noter le pseudo de l'élève que tu as aidé ou encore la question à laquelle tu as répondue afin de rechercher dans l'outil de recherche de la Zone!
En espérant que cela réponde à ta question. Si tu en as d'autres, n'hésite surtout pas à nous réécrire, il nous fera plaisir de t'aider à nouveau!
À bientôt,
Océane :)