Best Of

Pour le premier, voici comment procéder

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

et c'est toujours une bonne idée de regarder si tes calculs se tiennent (fais toi un graphe oui c'est plus long mais ta compréhension va en bénéficier)

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Note: sur Alloprof tu as plus de chances d'avoir des réponses à tes problèmes en faisant une requête pour chacun d'entre eux.

Pour la deuxième question :

La question concerne l’intersection d’un cercle et d’une parabole. Le cercle est défini par l’équation x exposant 2 + y exposant 2 - 1 = 0 et la parabole est définie par x exposant 2 = 4ay. Nous devons trouver toutes les valeurs réelles de a pour lesquelles la parabole et le cercle n’ont qu’un seul point en commun.

Pour résoudre ce problème, nous devons résoudre simultanément les deux équations. Cela signifie que nous devons trouver une valeur de a pour laquelle il n’y a qu’une seule solution à l’équation x exposant 2 + y exposant 2 - 1 = 0 et x exposant 2 = 4ay. C’est un problème complexe qui nécessite une compréhension solide des mathématiques, en particulier de l’algèbre et de la géométrie analytique.

Je vais essayer de simplifier le processus autant que possible. Voici comment nous pouvons procéder :

Exprimez y en fonction de x à partir de l’équation de la parabole : y = x exposant 2/(4a).

Remplacez y dans l’équation du cercle par l’expression obtenue à l’étape 1.

Vous obtiendrez une équation en x qui dépendra du paramètre a. Cette équation sera du second degré.

Un cercle et une parabole ont un seul point en commun si et seulement si l’équation du second degré obtenue à l’étape 3 a une unique solution. Cela se produit lorsque le discriminant de cette équation est nul.

Mettez le discriminant égal à zéro et résolvez l’équation obtenue pour trouver les valeurs de a.

Bonjour, je suis ravi de vous aider avec les devoirs de mathématiques de votre enfant. Pour la première question :

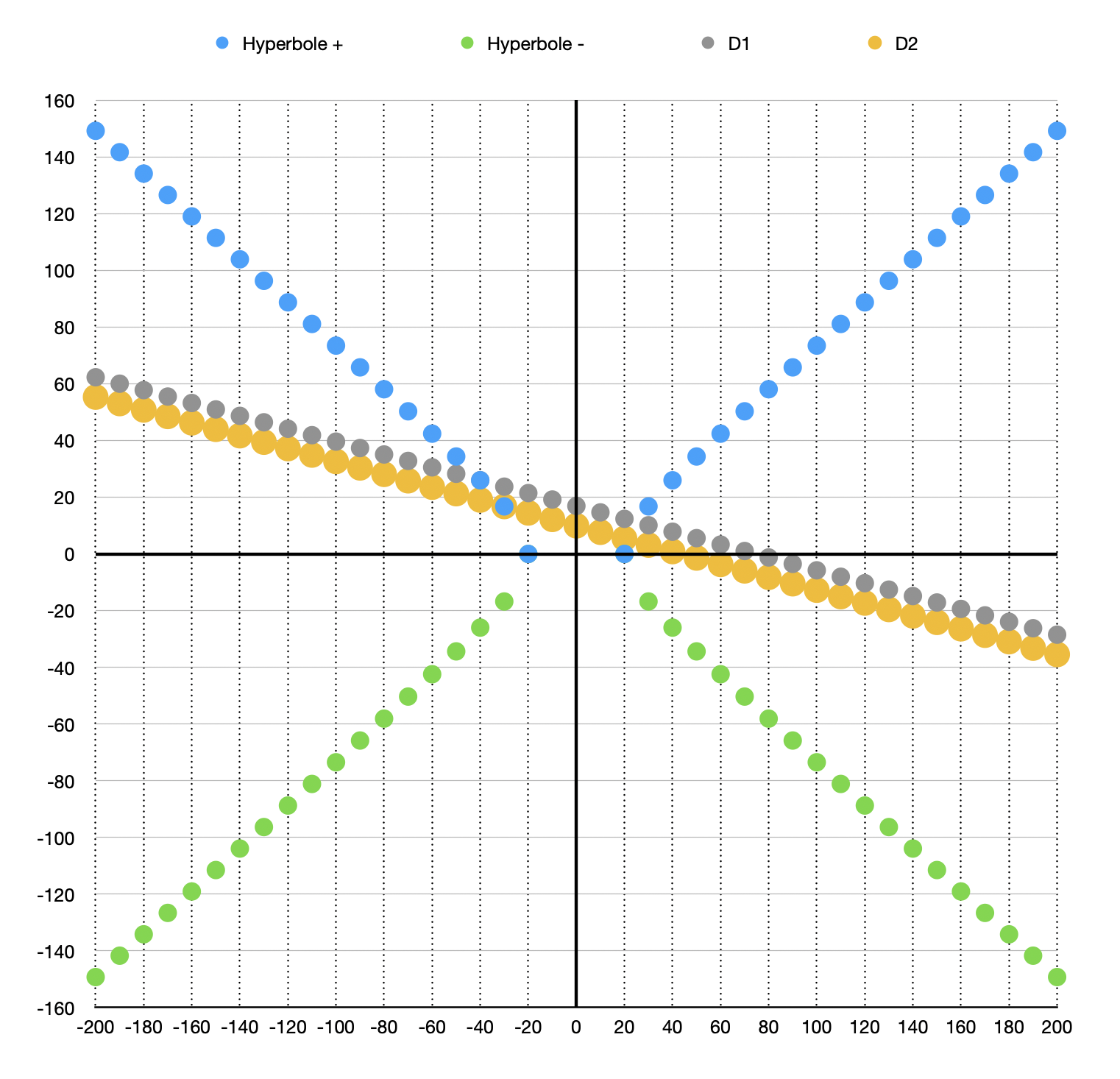
La question que vous avez partagée concerne une hyperbole dont l’équation est

x exposant 2 y exposant 2

-------------- (Fract.) - -------------- (Fraction)

400 225

Cette hyperbole est croisée par deux droites parallèles. L’une d’elles rencontre l’hyperbole aux points (-40, 15√3) et (25, -45/4). L’autre rencontre l’hyperbole en un point ayant -30 pour abscisse et un zéro positif.

Pour trouver les coordonnées du second point de rencontre de cette droite avec l’hyperbole, nous devons d’abord comprendre que puisque les deux droites sont parallèles, elles ont la même pente. Nous pouvons donc trouver la pente de la première ligne en utilisant les deux points donnés et l’utiliser pour trouver le deuxième point sur la deuxième ligne.

La pente (m) est donnée par la formule

y indice 2 - y

m = ---------------------------- (Fraction)

x indice 2 - x indice 1

En utilisant les points (-40, 15√3) et (25, -45/4), nous obtenons :

−45 ÷ 4 − 15√3

m = -------------- (Fraction)

25 − (−40)

Maintenant que nous avons la pente, nous pouvons utiliser le point (-30, y) sur la deuxième ligne pour trouver y. Nous savons que l’équation d’une ligne est donnée par

y - y indice 1 = m (x - x indice 1)

En substituant m, x et x_1 dans cette équation, nous pouvons résoudre pour y. Cela nous donnera les coordonnées du second point de rencontre de cette droite avec l’hyperbole.

Salut!

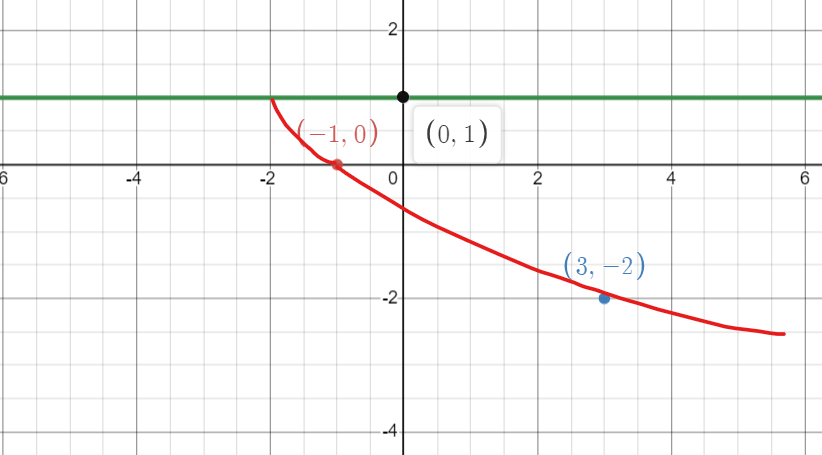
On sait que le paramètre k est 1, puisque le sommet est à y=1.

On te donne aussi 2 points de la fonction, soit (-1,0) et (3,-2).

En plaçant la droite y=1 (droite qui contient le sommet de la fonction) et les points donnés sur un graphique et en les reliant, on obtient ceci :

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Les points sont donc à droite du sommet à y=1, ce qui nous permet de conclure que b est positif.

Notre règle :

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

devient donc :

$$ f(x) = a\sqrt{+(x-h)} +1$$

$$ f(x) = a\sqrt{x-h} +1$$

Il nous reste 2 paramètres à trouver, soit a et h. On connait justement 2 points de la fonction. Il nous reste plus qu'à insérer les coordonnées de ces points dans notre règle, puis résoudre un système d'équations pour trouver a et h :

$$ 0 = a\sqrt{-1-h} +1$$

$$ -2 = a\sqrt{3-h} +1$$

Je te laisse terminer. J'espère que c'est plus clair pour toi! :)