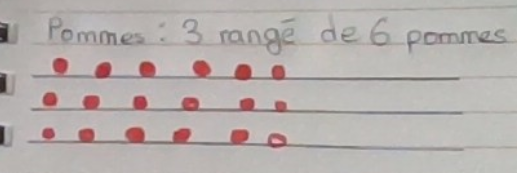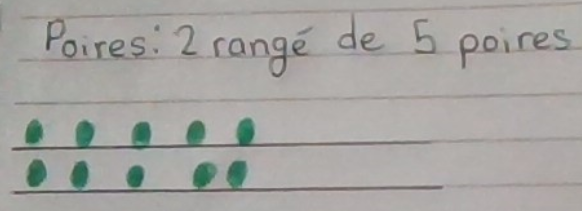Best Of

Salut Souris !

Premièrement, on vas commencer par combien y a-t-il de pommes au total. On sait qu'il y a 3 rangé de 6 pommes. Cela veut dire que dans chaque 3 rangé il y a 6 pommes. Voici un image :

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Donc pour savoir combien y a-t-il de pommes au total, on devait faire une multiplicatiton : 3 X 6.

Deuxiement, on sait qu'il y a 2 rangé de 5 poires et on devait trouver combien de poires y a-t-il au total.

Cela veut dire que dans chaque 2 rangé il y a 5 poires.

Voici un image :

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Donc pour savoir combien de poires y a-t-il au total on devait aussi faire une multiplication: 2 X 5.

Finalement, après avoir la réponse de 2 X 5 et 3 X 6, tu devait faire une addition pour savoir combien il y a de fruit en tout.

-Perche

on a la formule

Quand tu as une division d'un polynôme ou toute autre expression par une fraction, il faut considérer le polynôme ou l'expression au numérateur comme une fraction divisée par 1, et revenir a une grande fraction du type fraction divisée par fraction et appliquer la formule

(a/b):(c/d)=(ad)/(bc)

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Parce que le nombre positif et negatif sont possible. 5 au carré ca donne 25 et (-5) au carré ca donne aussi 25. Mathématiquement, en algebre mettons, il faudrait toujours indiquer les deux solution (ex. racine(25) = 5 ou -5)

Pourquoi on dit habituellement racine(25) = 5 ? Souvent la valeur négative n'est pas possible (hors du domaine) Par exemple, si jai une fonction qui me donne le volume de ma maison, le volume physique doit etre positif. Si tu veux etre exact il faudrait, dans ta résolution, que tu mentionnes les deux solutions possibles et que tu indiques que tu élimine une des deux et pourquoi.

Pour la fonction racine carrée, c'est une convention. C'est toujours un résultat positif parce que c'est définit ainsi.

Salut !

Désolé si tu n'as pas trouvé l'aide souhaitée !

Voici quoi consulter :

J'espère que le tout t'aidera, sinon réécris-nous !

Bonsoir bonsoir GalaxieEmpathique5265 !

Remarque que x + a apparaît à plusieurs reprises dans l'expression. On peut ainsi utiliser une substitution z pour simplifier l'expression :

$$ 2(x+a)^2+5(x+a)+2 $$

$$ 2z^2+5z+2 $$

Maintenant, il faut factoriser l'expression en utilisant la méthode produit-somme :

Pst! 4 et 1, car 4×1=4 et 4+1=5 ...

2z^2 + 4z + z + 2

2z(z+2) + 1(z+2)

Les deux termes ont un facteur commun de (z+2) :

(z+2)(2z+1)

Maintenant après avoir factorisé, il faut réintroduire x (x + a qu'on a remplacé par z) dans l'expression :

$$ (x+a+2)((2(x+a))+1) $$

Si on simplifie davantage :

$$ (x+a+2)(2x+2a+1) $$

Voilà !

De plus, je te présente notre fiche sur les méthodes de factorisation !

J'espère que le tout est plus claire maintenant !

Regarde le problème la tête reposée un peu plus tard.

Note que pour les vecteurs unitaires il y a plusieurs choix possibles: les coefficients qui les multiplient vont changer leur orientation.

Bonjour.

15: Quand tu fais une T1, il faut que la somme des deux nombres avec lesquels tu vas factoriser soit égale au B, ici 6. Après avoir trouvé une des possibilités, multiplie ensemble les deux nombres pour avoir ton C. Par exemple, 3+3 = 6, donc 3 et 3 peuvent être utilisés en facteurs dans x^2 + 6x + C. (x+3) (x+3) = x^2 + 6x + 9. 9 serait donc une de tes réponses, je te laisse trouver les autres.

Rappel: Les nombres naturels sont sans décimaux et positifs.

16 : Pour ne pas être mêlé, remplace (x+a) par x, factorise normalement, et remplace x par (x+a) à la fin.