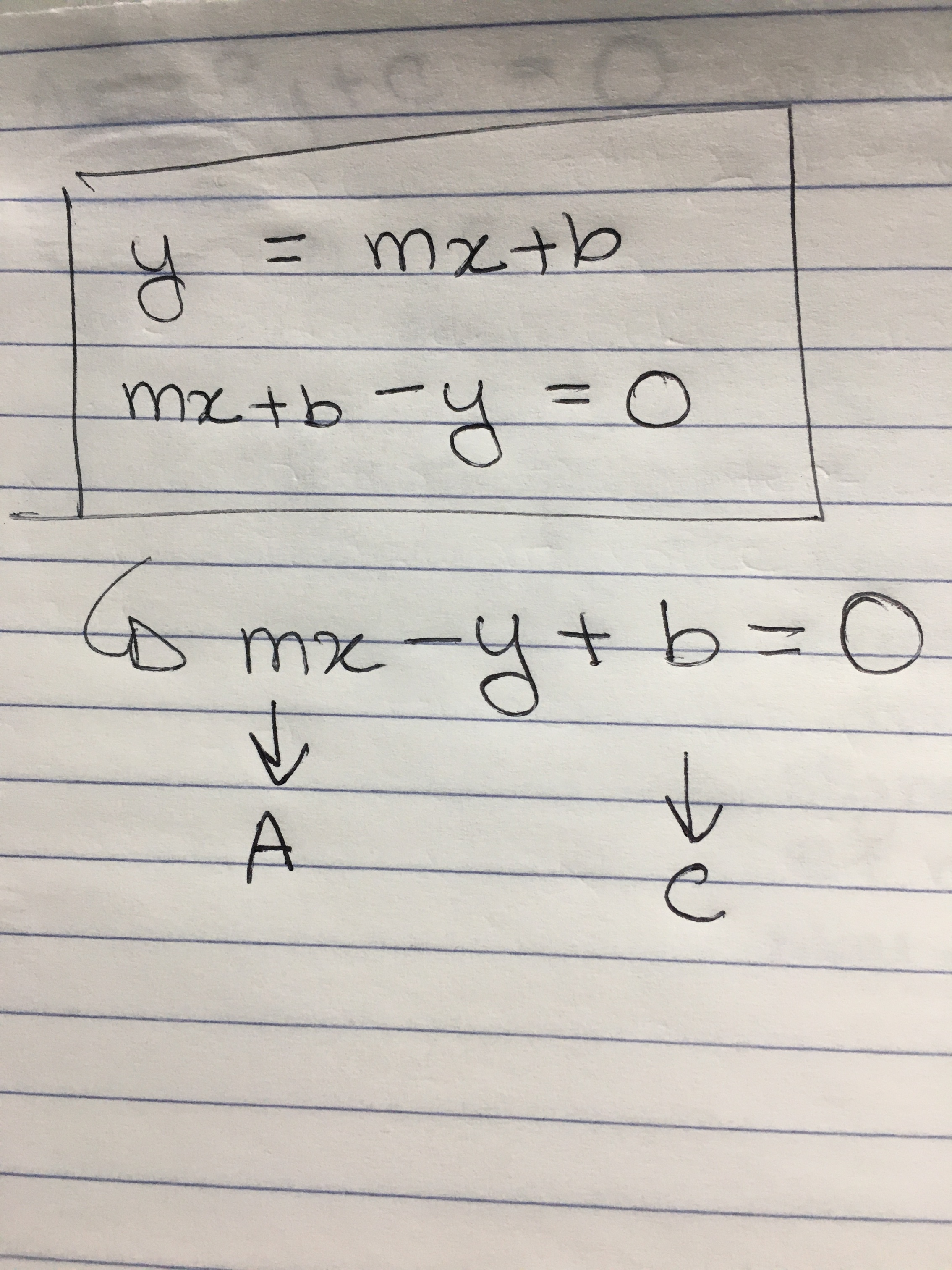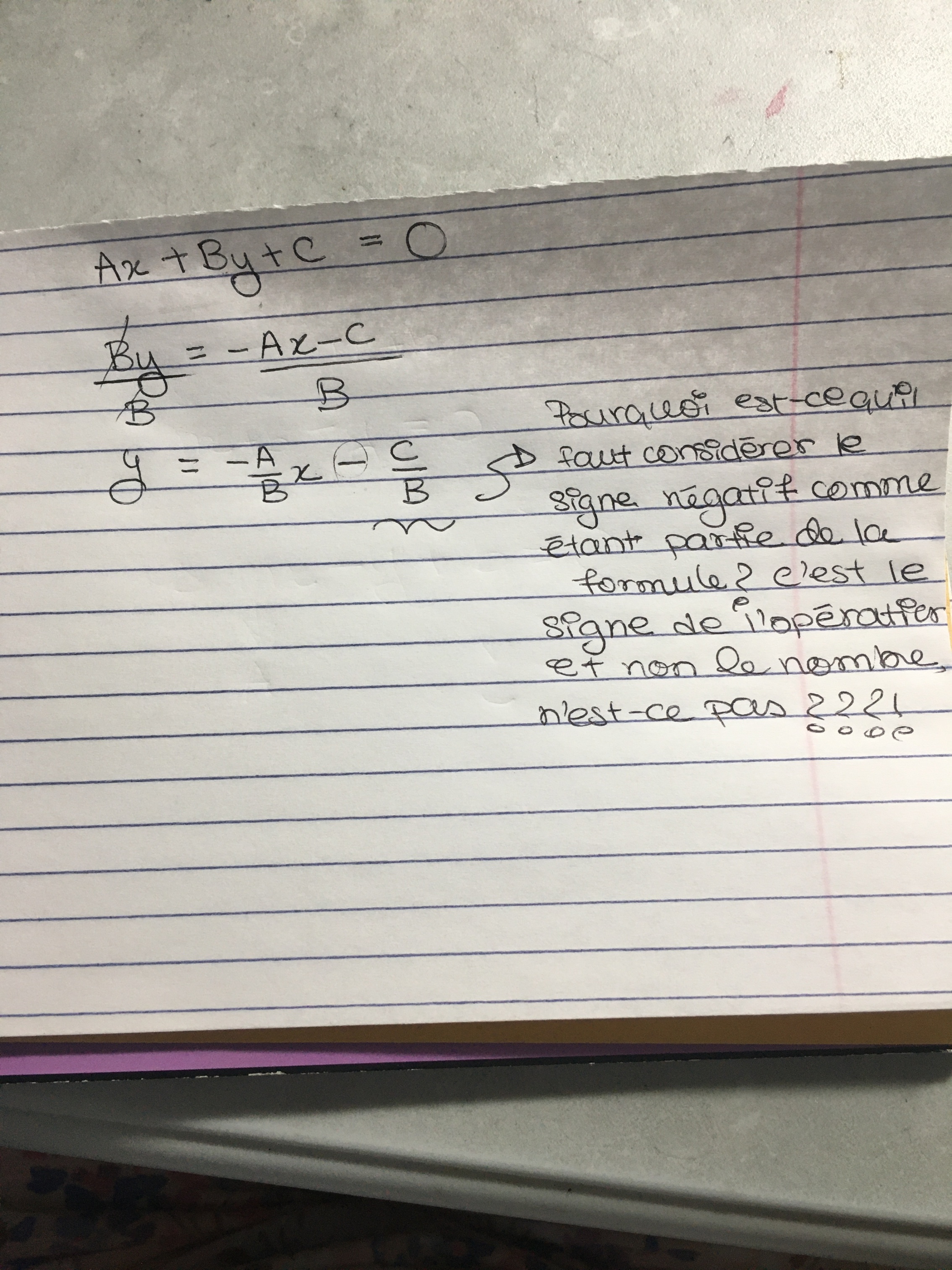Best Of
Question
Re-benjour!
Tout d'abord, merci beaucoup à Mme Katia de m'expliquer avec détail mes questions. Je commence à y voir un peu clair maintenant.
Pourtant, je voudrais clarifier mes autres doutes:
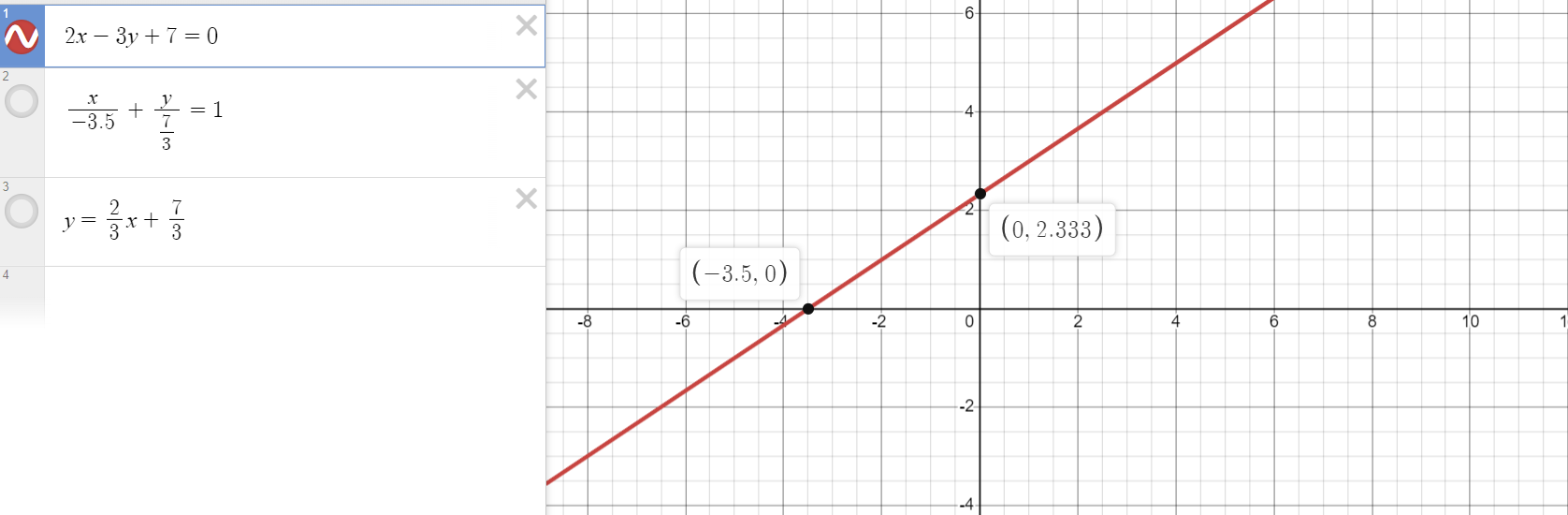
1) Comme vous l'avez dite, on a manipulé la même règle algébriquement pour avoir trois différentes formes qui représentent la même droite. Si c'est le cas, alors pourquoi est-ce dans la forme générale, on ne dit pas que A = m et C=b, puisqu'on a juste déplacé les nombres de l'autre côté de l'égalité? Pourquoi est-ce qu'on a placé de nouveaux coefficients (A,B et C) alors que c'est la même règle qu'on a manipulé? Si m n'est pas égale à A, donc comment j'obtinedrais la même droite, car la pente a changé.
Voici un essai que j'ai fait pour mieux représenter ma question:
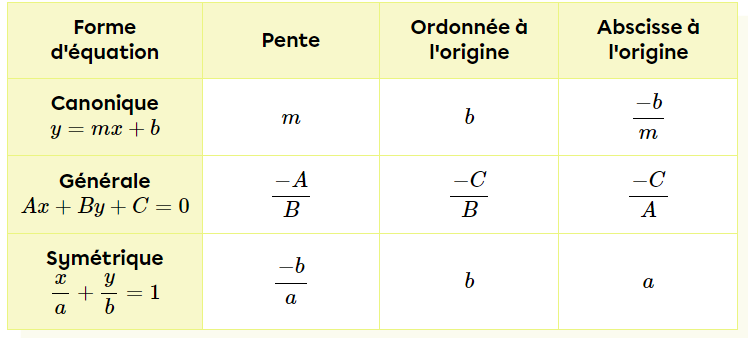
2) Par rapport au tableau qui résume les formules pour trouver les paramètres de l'équation, j'ai une GRANDE confusion: Pourquoi est-ce qu'il faut considérer/inclure le signe négatif comme étant partie de la formule pour calculer b (ordonnée à l'origine) ? C'est le signe de l'oprération et non le nombre, n'est-ce pas?
Voici une photo:
3) Je n'avais jamais pu poser cette question qui a été fortement ignoré par tous mes profs :( La voici:
Admettons que j'ai l'opération suivante:
12 - 5 (Si j'ai 12 chocolats, et que j'en soustrais 5, je ne vais pas dire que j'ai enlevé -5 chocolats. Sinon, ça devient 12- - 5).
Donc, ici, si le signe au milieu sert à indiquer l'opération à effectuer, soit la soustraction, alors comment est-ce que le signe négatif peut appartenir à 5? Mon prof m'avait dit que chaque nombre a son signe à gauche. Mais, je n'arrive toujours pas à comprendre comment un symbole d'opération mathématique peut appartenir à un nombre qui le suit? Quel serait donc le symbole mathématique? Est-ce qu'une signe joue ces deux rôles à la fois? J'en suis complètement mélangée.
4) Juste pour s'assurer: Les trois différentes formes de l'équation représentent la même droite car c'est la même règle écrite d'une manière différente, n'est-ce pas?
Désolée de vous achaler encore une fois.
Merci beaucoup pour votre aide Mme Katia et bonne soirée à vous! Je vais essayer de mon mieux de comrendre et d'appliquer vos conseils et supers explications.
Re: Question
Bonjour,
Ici tu dois trouver 3 nombres qui se suivent et dont la somme est 7 325.
ex trouver les trois nombres consécutifs dont la somme est 3003 :
1000 + 1001 + 1002 = 3003
À ton niveau, tu ne peux y aller que par essai-erreur et par logique.
Bonne journée
Re: Question
Tu l'as trouvé !
Ton raisonnement est juste.
Pour déterminer combien de tours chacune des roues a fait pour que les dents marquées en rouge se trouvent de nouveau vis-à-vis, nous pouvons utiliser le concept de "plus petit commun multiple" (PPCM) des nombres de dents de chaque roue.
La grande roue compte 33 dents, et la petite en compte 15. Le PPCM de 33 et 15 est le plus petit nombre de dents pour lequel les dents marquées en rouge se retrouveront en face l'une de l'autre.
Bonne journée :)
Re: Question
Merci pour ta question!
Tu peux prendre note que cet échange sera archivé à des fins d'amélioration de nos services et de recherche.
Rappelle toi que :
$$ 1\:mole = 6•10^{23}\:particules $$
Peu importe la particule en jeu, la quantité d'une mole est fixe.
Ainsi, la réponse à cette question est 6 x 10^23.
Cette fiche du site d'Alloprof explique la notion de mole :
N'hésite pas si tu as d'autres questions!
Re: Question
Bonjour,
La façon la plus simple, serait de prendre les nombres de départ soit 630, 450 et 270 et de les diviser par le nombre de boites (90) pour trouver la composition des boites.
donc,
450 / 90 = 5 n
270 / 90 = 3 b
630 / 90 = 7 l
Bonne journée :)
Re: Question
Salut à toi !
Merci pour ta question. :)
Par cet exercice, tu dois trouver le bon pronom (je, tu, il/elle, nous, vous, ils/elles) et accorder adéquatement le verbe qui l'accompagne.
Ainsi, si l'on prend le a), le verbe penser est accordé à la deuxième personne du singulier, soit tu. Il faut donc écrire "Quand penses-tu pouvoir donner un coup de main pour mon déménagement?".
Pour t'aider, je t'invite à consulter cette fiche !
N'hésite surtout pas à nous réécrire si tu as d'autres questions !
Océane :)
Re: Question
Salut!
Le nombre de participant du concours sera le nombre de gens qui posent une question, peu importe le nombre de questions qu'ils posent (alors même si tu poses 100 questions, tu as toujours une chance).
À chaque fois que tu poses une question, les professeurs d'Alloprof vérifient si ta question ne comprend pas de problèmes comme des niaiseries ou si c'est une question ayant un lien avec tes études.
Si ta question passe le ''test'', elle sera automatiquement vérifiée.
: )
Re: Question
Salut!
Tout d'abord, merci pour tes questions! Ça nous fait un grand plaisir de t'aider, et sache qu'il n'existe pas de questions insensées ou trop longues! ;)
1) Si les trois formes d'équation d'une droite (fonctionnelle, symétrique et générale) sont différentes les unes des autres, pourquoi est-ce qu'on peut passer d'une forme à l'autre?
On peut passer d'une forme à une autre parce qu'il s'agit toujours de la même droite! La forme est différente, c'est-à-dire que la façon d'écrire l'équation de cette droite est différente, mais cela reste toujours la même droite, il est donc normal que l'on puisse interchanger de forme avec quelques manipulations algébriques.
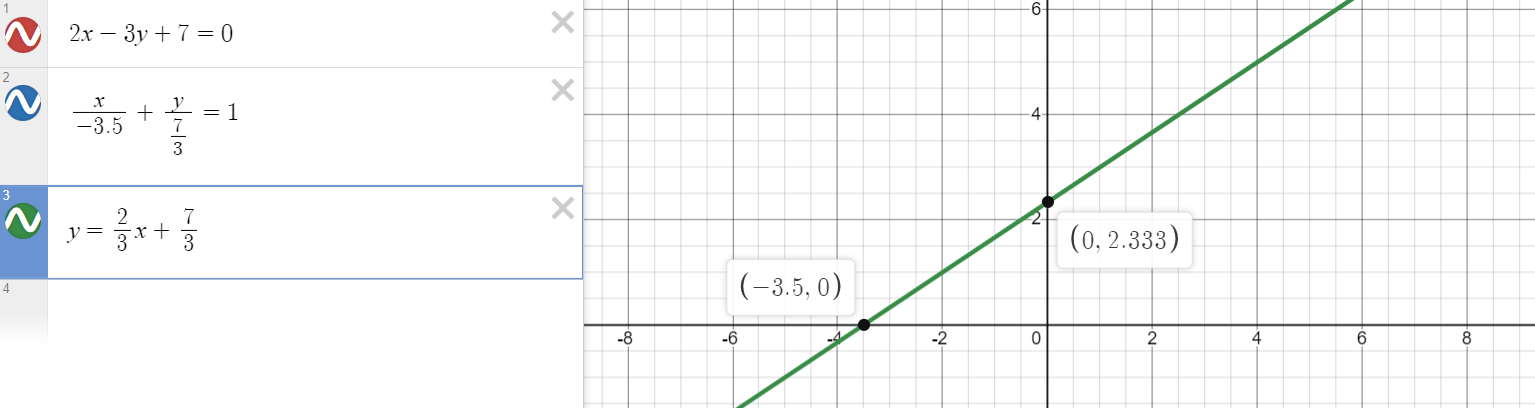
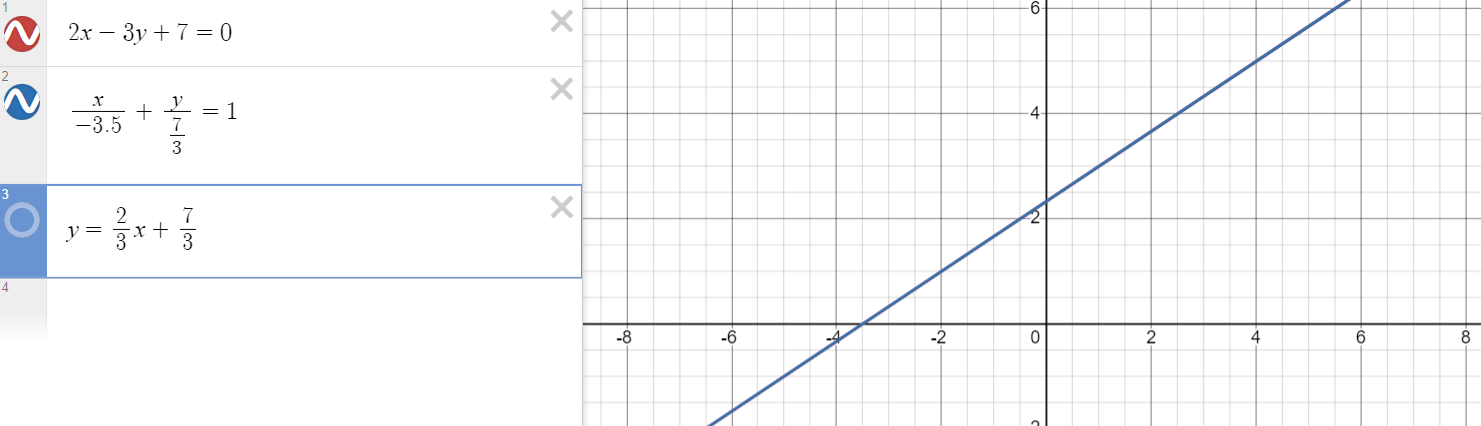
Si tu dessines le graphique d'une droite sous forme fonctionnelle, symétrique ou générale, tu obtiendras la même droite :
2) Comment les différentes formes de l'équation d'une droite peuvent donner la même valeur de x pour son y et vice-versa, lorsqu'on cherche les coordonnées? Si on passe d'une règle à l'autre, ça ne reste plus la même règle.
Faux, c'est la même règle, elle est juste écrite différemment! Puisque c'est la même droite, il est donc normal qu'on obtienne les mêmes coordonnées (x, y), peu importe la forme de l'équation choisie pour les calculer!
3) De plus, je ne comprends absolument pas lorsque mon prof répète que les trois formes de l'équation sont la même chose (mais la forme symétrique donne 1 comme résultat, la forme générale donne 0 et la forme fonctionnelle donne y).
Ton prof a raison. Lorsqu'il affirme que les trois formes de l'équation sont la même chose, il dit ainsi que ces trois formes représentent la même chose...la même droite!
Il ne faut pas que tu voies le côté droit de l'égalité comme un résultat. Ce n'est pas que la forme symétrique "donne 1 comme résultat", le 1 est là simplement pour permettre d'avoir l'abscisse à l'origine et l'ordonnée à l'origine comme dénominateur dans les fractions contenant les variables x et y, ce 1 ne veut rien dire en tant que tel, la droite n'est pas "égale à 1". Même chose pour la forme générale, le 0 permet de donner une signification à nos paramètres A, B et C, des paramètres qui nous permettent de calculer la pente, l'ordonnée à l'origine ou l'abscisse à l'origine. S'il y avait un autre nombre autre que 0, alors il ne s'agirait pas de la forme générale et donc les coefficients devant les variables x et y ne représenteraient pas nos paramètres A et B et ne voudraient rien dire, ils ne nous permettraient pas de calculer la pente, l'ordonnée à l'origine ou l'abscisse à l'origine.
Les différentes formes d'équations sont comme des moules que l'on utilise pour voir clairement certains paramètres de notre droite. La forme symétrique sert à identifier rapidement l'ordonnée et l'abscisse à l'origine et la forme canonique (fonctionnelle) permet de trouver sans calcul la pente et l'ordonnée à l'origine.
Par exemple, si on te demande de trouver la pente de la droite \( \frac{x}{3}+\frac{y}{4}=2\), tu pourrais décider de transformer le côté gauche de l'équation en un 1 afin d'obtenir la forme symétrique, puis calculer la pente avec les paramètres b et a (pente = -b/a). Tu pourrais également décider de transformer l'équation en forme canonique pour obtenir le paramètre m qui représente la pente, ou encore de transformer en forme générale et calculer la pente avec les paramètres -A/B. Dans tous les cas, tu obtiendras la même réponse. Voilà donc l'utilité des différentes formes d'écriture d'une droite.
Voici une fiche sur cette notion qui pourrait t'être utile : Les formes d'équation d'une droite | Secondaire | Alloprof
J'espère que c'est plus clair pour toi, sinon, n'hésite pas à nous réécrire! :)
Re: Question
Bonjour ! :) Quelle bonne question !
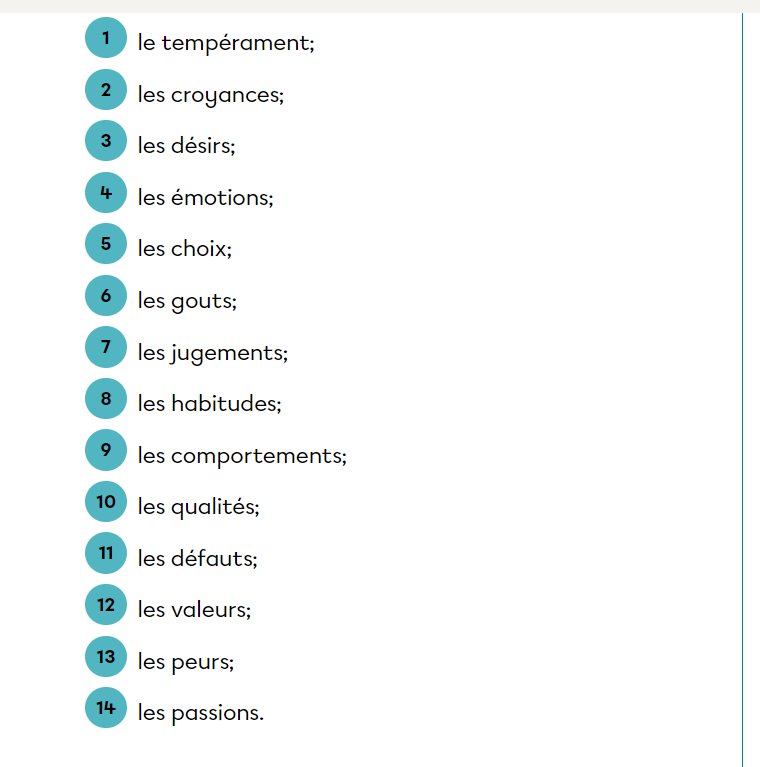
Les caractéristiques psychologiques d'un personnage regroupent BEAUCOUP de choses.
Je dirais que les traits de caractères seraient surtout les habitudes, goûts, tempérament et valeurs.
Un trait de caractère est quelque chose propre à une personne, peu importe le contexte. Certaines des caractéristiques psychologiques peuvent varier (ex : émotions).
J'espère que ça répond à ta question ! :D
Sarah G