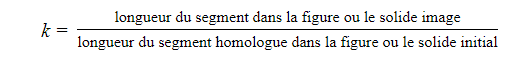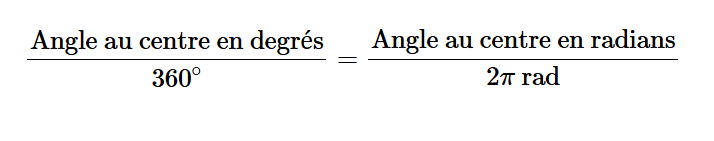Best Of
Re: Question
bonjour,
Le rapport entre la taille réelle et la taille sur le dessin est le même pour Malek et Tiffany:
\[ \frac{taille\ réelle\ de\ Malek}{taille\ sur\ le\ dessin\ de\ Malek}=\frac{taille\ réelle\ de\ Tiffany}{taille\ sur\ le\ dessin\ de\ Tiffany} \]
\[ \frac{168\ cm}{... \ mm}=\frac{?\ cm}{...\ mm} \]
Re: Question
Bonjour Jason,
Ici, il est question du rapport de similitude. Puisqu'on a affaire à des mesures de longueurs, celui-ci serait k.
Tu dois trouver le rapport k entre la mesure fictive et réelle de Malek.
Ce rapport se trouve comme suit:
Par la suite, utilise le produit croisé. Divise 142 (la mesure fictive de Tiffany) par le rapport trouvé pour calculer sa mesure réelle.
k/1 = 142 / mesure réelle de Tiffanny
Je t'invite à consulter la fiche Les rapports de similitude, d'aire et de volume (k, k², k³) | Alloprof .
Merci pour ta question ! Au plaisir d'avoir pu t'aider :)
Re: Question
Bonsoir WapitiAlpha6501! 😊
Merci pour ta question!
Tu as bien remarqué que les molécules n’ont pas les mêmes propriétés que les atomes qui les composent. Et c’est tout à fait normal! 😉
Quand deux atomes se lient ensemble, ils échangent ou partagent des particules qu’on appelle des électrons.
Les électrons, ce sont de toutes petites particules qui tournent autour du noyau de l’atome.
Ces électrons sont super importants, car ce sont eux qui déterminent le comportement chimique des atomes.
Par exemple :
- Si un atome perd des électrons, il va se comporter d’une certaine façon,
- Tandis qu’un atome qui gagne des électrons va avoir un comportement différent!
Et une fois qu’ils sont liés ensemble dans une molécule, ils ne réagissent plus du tout comme avant.
- C’est pour ça que les molécules ont des propriétés nouvelles, qui correspondent aux propriétés des nouvelles atomes mais qui sont différentes de celles des atomes pris séparément.
J’espère que ça t’aide à mieux comprendre! 😊
N’hésite pas à revenir si tu as d’autres questions!
Bonne soirée! 🌙
Re: Question
Salut Kali,
Merci pour ta question!😊
À partir de l'aire totale, tu peux retrouver la mesure de l'aire latérale en faisant la soustraction entre l'aire totale et l'aire des bases.
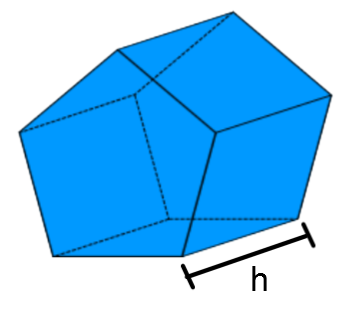
À partir de l'aire latérale, tu peux retrouver la hauteur de ton solide, puisqu'un côté correspond à cette hauteur. Voici un exemple :
Si tu as l'aire de la base, tu peux retrouver la mesure d'un des côtés du rectangle qui forme une partie de l'aire latérale avec la hauteur.
Tu dois isoler une variable dans l'équation, voici comment faire. La formule de l'aire de la base dans cette situation correspond à :
Si tu utilises la formule avec les informations qui te sont fournies dans ton énoncé, tu as un seul inconnu qui doit trouver. Disons que, dans notre situation, on recherche la mesure d'un côté du polygone, c'est-à-dire la variable c.
Pour trouver sa valeur, tu dois remplacer dans la formule les données qui te sont fournies et faire les opérations inverses afin d'avoir une équation sous la forme c = ...
Posons cette équation comme exemple :
$$10 = \frac{2\times3\times c}{2}$$
La première étape serait de multiplier par deux des deux côtés afin de retirer la division par deux à droite. On obtient :
$$20 = 2\times3\times c$$
Si on fait la multiplication devant le c, on obtient ceci :
$$20 = 6 \times c$$
On fait la division par 6 des deux côtés pour isoler 6, on obtient :
$$\frac{10}{3} = c$$
Nous avons isolé la variable c.
Dans notre situation, nous avons maintenant la mesure du côté qui forme le rectangle de l'aire latérale. Il nous reste plus qu'à isoler la variable h avec l'aire du rectangle. Le principe est le même que pour l'exemple plus haut.
J'espère que ça t'aide et n'hésite pas à nous réécrire si tu as d'autres questions!😉
Anthony B.
Re: Question
Bonjour, AvocatInoubliable4560!
Tu dois regarder la base de la pyramide. Pour la première en haut, la base est un triangle, donc la pyramide va être à base triangulaire. Ta réponse va dépendre de la forme que ta pyramide avait à la base.
Re: Question
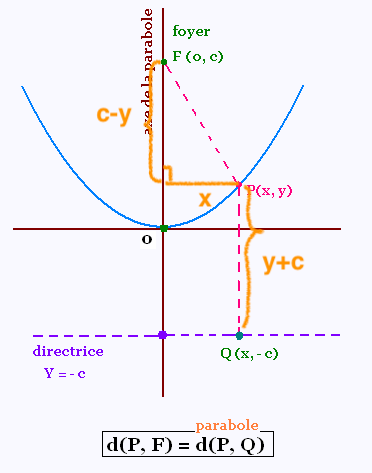
Pour prouver que d(P,F) = d(P,Q)
ou encore mFP = mPQ pour un point quelconque (x,y) sur la courbe
on a mFP² = (c-y)² + x²
et mPQ² = (y+c)²
donc mFP² = mPQ²
si et seulement si (qu'on représente par le symbole <=>)
(c-y)² + x² = (y+c)²
<=> c² -2cy + y² + x² = y² + 2cy + c²
<=> -2cy + x² = 2cy (après simplification)
<=> x² = 4cy
qui est vrai puisque c'est l'équation de la courbe: la parabole centrée à l'origine de foyer (0,c)
donc l'énoncé initial (d(P,F) = d(P,Q)) est vrai
Re: Question
Bonsoir OpaleTurquoise456! 😊
Merci pour ta question!
Commençons par bien identifier les données :
- La distance focale (lf) est de 9 cm. Comme il s’agit d’un miroir divergent, on n’oublie pas que cette valeur est négative : donc lf = -9 cm.
- La hauteur de l’objet (ho) est de 6 cm.
- Le grandissement est 3 fois plus petit, donc G = 1/3 = 0,33.
Ce qu’on cherche, c’est la distance de l’objet (do). Pour y arriver, on va passer par quelques étapes!
En regardant les formules disponibles ici:https://www.alloprof.qc.ca/fr/eleves/bv/physique/les-equations-des-miroirs-p1045 , on voit que :
do = lo + lf
Mais ici, il nous manque lo, soit la distance de l’image. Heureusement, on peut la trouver grâce à la formule du grandissement :
G = -lf / lo
On remplace :
0,33 = -(-9) / lo
Donc :
lo = 9 / 0,33 = 27 cm
Maintenant qu’on connaît lo, on peut revenir à la formule de départ :
do = lo + lf
do = 27 + (-9) = 18 cm
Ton objet est donc placé à 18 cm de ton miroir!
J’espère que ça t’aide! Si tu as d’autres questions, n’hésite pas à revenir nous voir, on est toujours là pour toi. 😊
Bonne soirée! 🌙
Re: Question
Bonjour OpaleTurquoise456,
Merci d'utiliser la Zone d'entraide !
Pour un miroir convexe, la distance focale est négative. Ici, on a : f=-25 cm
L'image se forme derrière le miroir à 11 cm, ce qui veut dire d= -11 cm
( Signe négatif, car par convention, on prend comme positif le côté '' réel'' devant le miroir )
La formule du miroir est : 1/f=1/d ( distance de l'objet au miroir ) + 1/d (distance de l'image au miroir )
Le grandissement s'exprime ainsi : M= hi ( hauteur de l'iamge/ ho (hauteur de l'objet = 6,0 cm)
En effectuant les calculs pour trouver la distance de l'objet et le grandissement , on obtient environ 3,36 cm.
Voici une fiche explicative : https://www.alloprof.qc.ca/fr/eleves/bv/physique/les-miroirs-plans-p1043
Félicitations, tu avais raison !
N'ésite pas à revenir nous voir si tu as d'autres questions :)
CigogneNoble4278
Re: Question
Merci pour ta question!
Pour la partie b, tu peux utiliser les valeurs de 11,89 et 18,29 m afin de trouver les orientations maximales et minimales que doit avoir la balle afin de toucher le sol à cette distance.
Commençons par transformer la vitesse de 160 km/h en m/s :
$$ 160\:km/h = 44,44\:m/s $$
Établissons ensuite les composantes de la vitesse en x et en y en fonction de l'angle d'inclinaison du service (theta) :
$$ v_x = 44,44cos(\theta) $$
$$ v_y = 44,44sin(\theta) $$
Puis, trouvons l‘expression du déplacement de la balle horizontal :
$$ 11,29 = 0 + 44,44cos(\theta)t $$
Puis, trouvons l'expression du déplacement vertical :
$$ 0 = 1 - 44,44sin(\theta)t + \frac{1}{2}(-9,81)t^2 $$
On doit trouver la valeur de theta qui fait en sorte que les deux expressions sont simultanément vraies. Pour ce faire, isolons t dans chaque équation :
$$ t = \frac{11,29}{44,44cos(\theta)} $$
$$ t = \frac{44,44sin(\theta) ± \sqrt{(44,44sin(\theta))^2-4•1•(-4,90)}}{2•1} $$
Puis, tu peux établir une égalité entre les deux valeurs de t et isoler la valeur de theta! Tu peux faire la même chose pour la valeur de 18,29 m pour trouver l'angle minimal.
Cette fiche du site d'Alloprof explique la résolution de systèmes d'équation linéaire :
N'hésite pas si tu as d'autres questions!
Re: Question
Bonjour OrComique4346,
Merci pour ta question :)
La première chose à faire pour résoudre ces questions est de localiser les valeurs en terme de radians. Par exemple, on sait que pi ≈ 3,14 te que 3pi/2 ≈ 4,71. Comme pi < 4 < 3pi/2, ça signifie que cette valeur se trouve dans le troisième quadrant!
Tu peux aussi convertir l'angle (qui est en radian) en degrés pour mieux le situer dans le plan cartésien. Tu peux faire cela avec cette formule:
Par exemple, 4 rad équivaut à environ 229,18◦.
N'hésite pas si tu as d'autres questions :)
Sandrine