Best Of
Re: Question
🤨 uh oh
Au centre centre de la terre, il y a le noyau
🟡
Ce qui entoure le noyau est le manteau
🟠🔥
Et la lithosphère est l'enveloppe de la terre.
🟤🌳🌴
Je pense pas que ça aide, mais c'est au cas où que tu ne sais plus c'est quoi la lithosphère 🫥
Ah- voici l'explication meilleure⬇️:
Re: Question
Avec de la pratique tu peux les connaitre.
Astuce pour les connaitre:Tu prends une table, exemple la table de 6.
Tu écris sur une feuilles: 6x1, 6x2, 6x3.... jusqu'a 12.
Ensuite tu trouves les reponses, tu regardes ou ta fait tes fautes et tu recommences la meme table jusqu'a temps que tout soit bon.
J'espere que ca a pu t'aider! (J'ai utilisée cette technique de la répétion pour les apprendre et ca marche!)
Bonne soirée! :)
Re: Question
Salut à toi brave moussaillon! 😁
Ça nous fait plaisir que tu utilises Alloprof!
Le numéro 1 est bon. Pour les autres, il semble y avoir plusieurs erreurs. Ce n'est pas grave, on recommence!
Je te montre un technique peut-être plus rapide ici!
Prenons le numéro 2 en exemple.
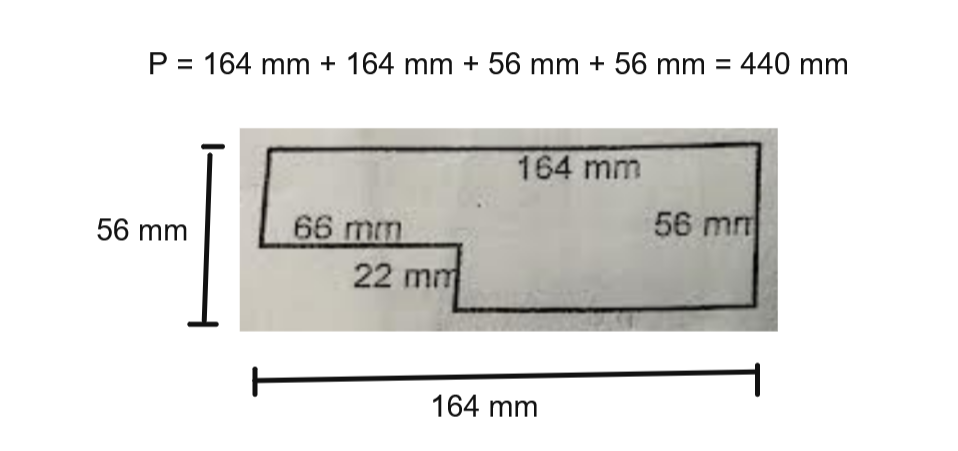
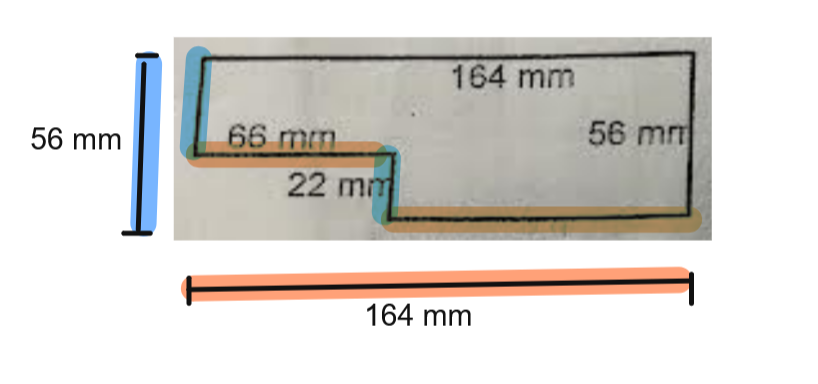
Vu que la somme des deux petits côtés donne 56 mm et que la somme des deux grands côtés donne 164 mm, on peut directement faire 164 mm + 164 mm + 56 mm + 56 mm pour trouver la mesure du périmètre.
Je te le montre plus en détails ici.
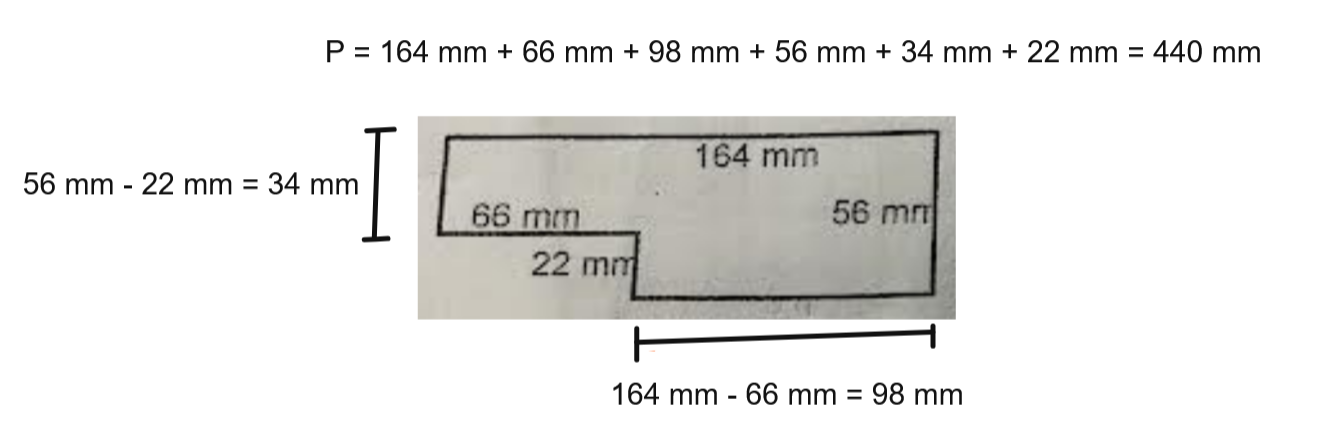
Il y aurait un autre moyen en calculant les soustractions pour trouver les réelles valeurs de tous les côtés, mais c'est plus long et ce n'est pas nécessaire pour trouver le périmètre. Ce le serait pour l'aire en contrepartie. C'est sûr que ça donne le même résultat!
On le fait.
Tu vois, ça donne le même résultat, mais la chaine d'opérations est plus longue pour trouver le périmètre et ça demande deux étapes de plus pour calculer les côtés manquants.
Je te laisse faire les corrections! Courage, ça va le faire!
Écris-nous si tu as d'autres questions. 😊
À bientôt sur la Zone d'entraide! 😎
Re: Question
Salut à toi brave moussaillon! 😁
Ça nous fait plaisir que tu utilises Alloprof!
D'abord, je te laisse ici une gamme de vidéos super pour réviser.
Si les récupérations sont disponibles sur l'heure du midi en sciences, tu pourrais toujours demander de l'aide à ton enseignant.e.
Sur cette fiche, tu pourras consulter toutes les étapes afin de manipuler adéquatement un microscope (dans la section Manipulations). Il faut vraiment y aller étape par étape pour un maximum de précision.
Écris-nous si tu as d'autres questions. 😊
À bientôt sur la Zone d'entraide! 😎
Re: Question
Bonjour!
Le dernier monde de Magimot est un peu différent. En effet, il n'a pas de fin! Tu peux continuer de jouer jusqu'à ce que tu n'aies plus de vie. Le but est de tuer le plus de monstres possible! :D
Si tu as d'autres questions, n'hésite pas à nous réécrire. Nous te répondrons avec plaisir!
Laurie :)
Re: Question
Salut PerleAdorable!
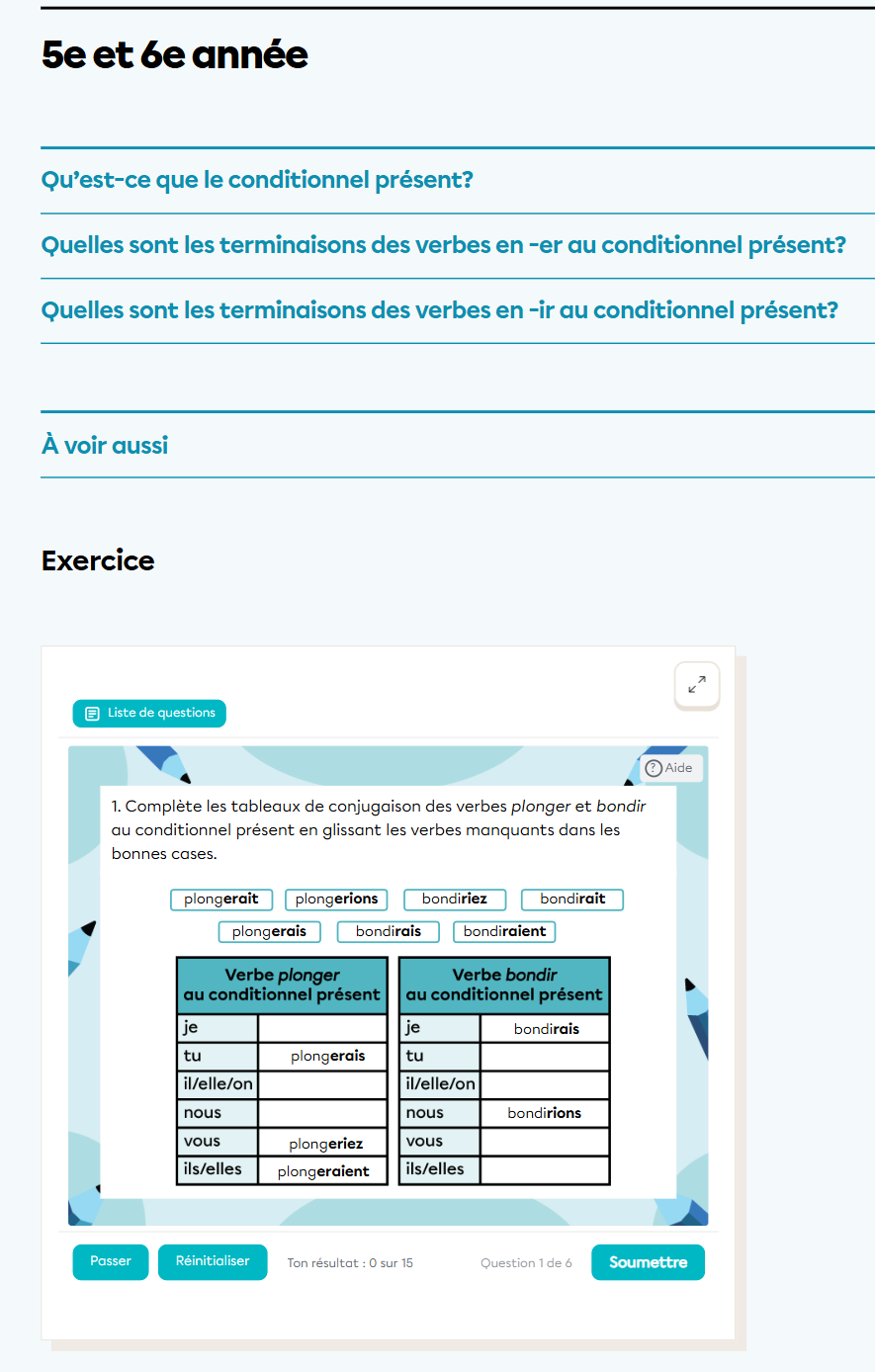
Je te suggère 2 pages vraiment complètes pour ces 2 temps de verbes. Je te laisse un aperçu de ce qui est couvert avec ces pages :
https://www.alloprof.qc.ca/fr/eleves/bv/francais/le-conditionnel-present-primaire-f1888
Reviens-nous si tu veux des conseils plus pointus!
Andréanne et l'équipe d'AlloProf! :)
Re: Question
Bonjour PerleAdorable,
Merci de faire appel à la zone d'entraide,
La plupart des verbes du 1er groupe utilisent pour le futur simple:
-erai
-eras
-era
-erons
-erez
-eront
comme terminaison et:
-erais
-erais
-erait
-erions
-eriez
-eraient
comme terminaison du 1er groupe au conditionnel présent.
Bonne étude.
ZincZen pro de la zone d'entraide.
Re: Question
Bonjour AnanasJaune9863,
Merci pour ta question :)
La masse de ta voiture peut influencer plusieurs facteurs. Par exemple, une voiture plus légère réduit la friction et permet de parcourir une plus grande distance. Une voiture plus lourde en revanche permet plus de stabilité et offre une meilleure traction (adhérence des roues).
En effet, si la voiture est trop légère, elle risque de patiner (perte de traction) ou d’être déséquilibrée. Mais si elle est trop lourde, l’énergie de la trappe à souris sera insuffisante pour la faire avancer loin. Le mieux est donc de chercher un équilibre en testant et en ajustant la masse afin d'avoir une performance optimale!
N'hésite pas si tu as d'autres questions :)
Sandrine
Re: Question
Bonjour DiplodocusDelta7583,
Merci pour ta question :)
Le cycle de la lithosphère est un processus continu d’expansion, de transformation et de recyclage des plaques tectoniques. Il joue un rôle dans l’évolution de la surface terrestre et dans la formation des reliefs. Plusieurs phénomènes contribuent à ce cycle:
- Formation de la lithosphère au niveau des dorsales océaniques
- Destruction et recyclage de la lithosphère lorsqu'il y a subduction des plaques
- Érosion qui peut entrainer la formation de nouvelles roches sédimentaires
- Volcanisme qui participe à la création de nouvelle croûte
Tous ces processus dynamiques transforment et renouvellent les roches et les plaques lithosphériques au fil du temps.
N'hésite pas si tu as d'autres questions :)
Sandrine
Re: Question
Salut!
Oui, c'est la bonne réponse, bon travail! :)
Si tu as d'autres questions, n'hésite pas à nous réécrire! :)