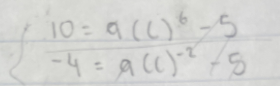Best Of
Re: Question
Bonjour, il existe différents types d'alimentation qui diffèrent selon l'espèce de mammifère. Certains sont herbivore et d'autres carnivores.
ChevalSociable6277
Question
Dans quel type d'eau (eau salée ou eau douce) y a-t-il un risque de noyade plus élevé ?
Re: Question
Salut LionCalme8200 😁
Merci pour ta question!
Il y a d'abord le baleineau, le bébé baleine, né de l'accouplement. C'est assez similaire à l'être humain, car les baleines sont aussi des mammifères! Le temps de gestation (bébé dans le ventre de la mère) est presque le même (10-12 mois), un peu plus long de trois mois.
La femelle accouche environ 1 fois tous les 2-3 ans. Ce bébé mesure déjà 7 m! (TechnoSciences, 2025)
Ensuite, la baleine atteint sa maturité sexuelle à environs 5 ans. Puis, peut faire des bébés à son tour.
Apprends-en plus sur la baleine ici.
Écris-nous si tu as d'autres questions. 😊
À bientôt sur la Zone d'entraide! 😎
Re: Question
Bonsoir! :)
C'est parce qu'ils n'ont pas de jambes!
(une petite blague hihi!).
De manière plus sérieuse, je peux te dire que les jeux fonctionnent de mon côté. Pourrais-tu nous réécrire en nous disant quel jeu ne fonctionne pas pour toi et quel est le type d'appareil que tu utilises (tablette ou ordinateur) svp? :)
À tout de suite!
Sarah G
Re: Question
Bonsoir! :) Merci de faire appel à nos services!
Voici quelques trucs pour s'améliorer en orthographe:
- Lire!!! Plus tu vois des mots, plus tu auras tendance à t'en souvenir. :)
- Varier tes techniques d'études. Tu peux réécrire tes mots, les épeler à voix haute, te faire poser des questions par tes parents, te confectionner des petites cartes de style «jeu de mémoire».
- Jouer à nos jeux éducatifs! Magimot en est un! https://www.alloprof.qc.ca/fr/eleves/bv/jeux/magimot
Nous te partageons plusieurs autres trucs dans la fiche suivante: https://www.alloprof.qc.ca/fr/eleves/bv/francais/ameliorer-sa-competence-d-ecriture-f1398
Tu es capable! :D
Si tu as d'autres questions, n'hésite pas à nous écrire!
Sarah G
Re: Question
Bonjour PamplemoussePacifique,
Merci pour ta question!
Chaque point du graphique de la vitesse en fonction du temps correspond à une vitesse instantanée aux temps t = 1s, t = 2s, etc.
Pour trouver cette vitesse instantanée, il suffit de diviser le changement de position par l'intervalle de temps correspondant.
Pour plus d'informations:
N'hésite pas si tu as encore besoin d'aide:)
Kylan
Re: Question
Bonjour FraiseAdorable5247,
Merci pour ta question :)
Une bonne façon de visualiser ce phénomène est de l'analyser sous deux angles: scalaire et vectoriel.
La première chose à observer est que la vitesse vectorielle initiale est de -5 m/s: cela signifie que la vitesse est de 5 m/s dans le sens négatif de l'axe des x. La vitesse finale quant à elle est de -2 m/s, donc la voiture va à la fin à 2 m/s dans le sens négatif de l'axe des x.
D'un point de vue scalaire, lorsqu'on regarde simplement la grandeur des vitesses, on voit que la voiture passe de 5 m/s à 2 m/s, c'est-à-dire qu'elle va de moins en moins vite ou qu'elle décélère.
Comme le signe des vitesses est négatif, on peut affirmer que la voiture décélère pendant qu'elle roule dans le sens négatif de l'axe des x :)
N'hésite pas si tu as d'autres questions :)
Sandrine
Re: Question
C'est tes fractions. Donc si j'ai comme expression 4/8, je peux simplifier cette fraction et la réponse serait de 1/2. Car si je divise 4 par lui-même et 8 par 4 j'obtiens 1/2. Tu dois avoir les plus petit chiffre en bref en haut et en bas.
Re: Question
Salut!
Il s'agit d'une fonction exponentielle, puisque l'asymptote est horizontale. :)
Ta démarche débute bien, tu essaies de résoudre le système d'équations suivant, ce qui est la bonne chose à faire.
Cependant, tu ne peux pas éliminer les -5 en divisant les équations (on additionne 5, on ne le multiplie pas).
Tu dois d'abord rassembler les constantes dans chaque équation :
$$ 10=a(c)^6 - 5$$
$$ 10+5=a(c)^6 - 5+5$$
$$ 15=a(c)^6 $$
et
$$-4=a(c)^{-2}-5$$
$$-4+5=a(c)^{-2}-5+5$$
$$1=a(c)^{-2}$$
Tu peux donc résoudre le système :
$$ 15=a(c)^6 $$
$$1=a(c)^{-2}$$
Je te laisse terminer le calcul. Si tu as d'autres questions, n'hésite pas! :)