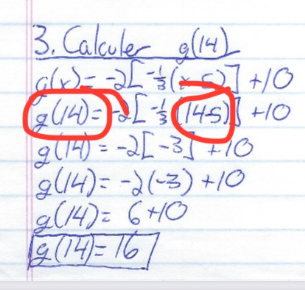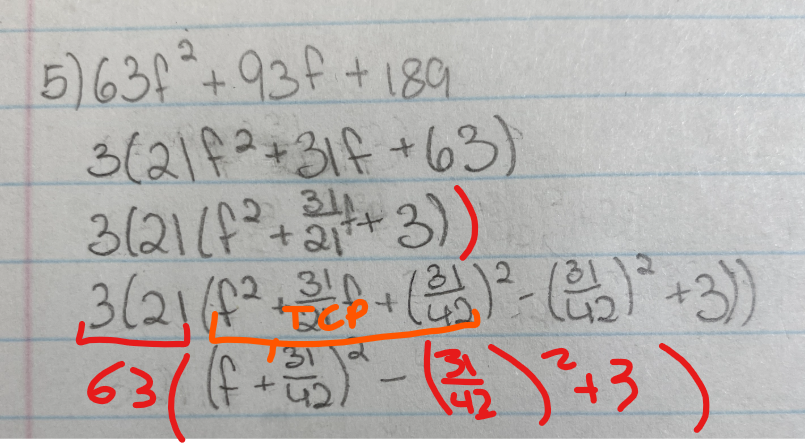Best Of

Salut !

La pondération des examens du ministère valent pour 10% de la note finale pour la sixième du primaire. Autrement dit, si tu as de bonnes notes pendant ton année scolaire, tu devrais réussir ta sixième année.

Si tu as d'autres questions, n'hésite pas !

ne tiquiète pas tu ne va pas redoubler juste pour cet exam les examen du minister ne valent que 10 % de ta note finale a la troisième étapes donc non tu ne va pas redoubler pour sa.

*ps: ses ma prof qui me la dis donc ses professionel se que je te di ;)

jéspère tavoir aidé bye

Bonjour! Je suis en 6e année et comme vous savez nous avons nos examens de minister. Alors aujourdhui on a eu un examen de minister de math et moi je suis sur que jai eu moitié faux. Alors si jai une tres mauvaise note dans cette examen mais dans mes autres examens de minister ( francais et maths) jai des bonne notes comme 80 - 90 est ce que cest possible de repeter notre 6e année? Ah oui et cette examen etait un resolution de problem ou on avait droit au calculatrice et aide memoire. SVP repondez le plus vite possible. Merci Je stress beacoup Svp quelqun repond vite jattend depuis 1 heur

Bonjour à toi!

Merci de faire appel à nos services :D

Dans un problème comme celui-ci, il est nécessaire de construire une équation algébrique!

La première étape est de poser les variables. Dans ce cas, il y a deux nombres de pièces que tu ne connais pas: le nombre de pièces de 10 sous, le nombre de pièces de 5 sous et le nombre de pièces de 25 sous. Le plus facile afin de choisir une variable est de trouver le nombre de pièces qui lie les trois ensemble. Je m'explique! Dans le nombre de pièces de 25 sous, ils font référence au nombre de pièces de 10 sous et dans le nombre de pièces de 5 sous, ils y font référence également. Il s'agit donc d'une bonne variable!

Par la suite, il faut déterminer toutes nos équations algébriques, en fonction de l'énoncé.

Ainsi, sachant que x= nombre de pièces de 10 sous, on peut établir que:

1/2 x = nombre de pièces de 5 sous

x + 6 = nombre de pièces de 25 sous

Finalement, tu dois te poser la question: comment je peux trouver ma valeur de x? Qu'est-ce qui relie tous mes équations? Dans ce cas, il s'agit du montant total! Il faut construire la dernière équation, qui comprend:

(Le nombre de pièces de 5 sous x 0,05$)+(le nombre de pièces de 10 sous x 0,10$) + (le nombre de pièces de 25 sous x 0,25$)+ (le nombre de pièces de 1$ x 1$) + (le nombre de pièces de 2$ x 2$)= montant total

Tu remarqueras que j'ai mis les 5 sous en dollars! Il est important de le faire, pour avoir la même unité partout.

Je te laisse compléter le numéro en effectuant la méthode de la balance pour trouver la valeur du x.

N'hésite pas si tu as d'autres questions, ce sera un réel plaisir pour moi de t'aider :D

Élizabeth

Salut!

En fait, on ne prend pas le couple (3, 10) spécifiquement pour trouver le k et (10, 14) spécifiquement pour trouver le a, il n'y aurait aucune logique qu'un couple soit choisit pour trouver un paramètre et pas l'autre.

Dans notre règle, il y a 2 paramètres manquants, soit a et k. Puisqu'on connait 2 points, on peut donc insérer les coordonnées de ces points dans l'équation, puis résoudre un système d'équations pour trouver les deux inconnus :

$$10=a[-\frac{1}{3}(3-5)]+k$$

$$14=a[-\frac{1}{3}(10-5)]+k$$

En résolvant ce système d'équations, on peut trouver a et k.

Or, ce qui arrive ici, c'est que dans la première équation, notre partie entière se simplifie jusqu'à obtenir 0, ce qui fait en sorte que le paramètre a est éliminé, et donc la première équation nous donne directement la valeur de k, donc la résolution du système est plus rapide qu'à l'habitude.

Si on avait plutôt eu, par exemple, les points (12, 10) et (10, 14) , alors on aurait eu ceci :

$$10=a[-\frac{1}{3}(12-5)]+k$$

$$14=a[-\frac{1}{3}(10-5)]+k$$

En simplifiant les deux équations, on a :

$$10=-3a+k$$

$$14=-2a+k$$

On résout ensuite ce système avec la méthode de résolution de notre choix (comparaison, substitution, réduction) pour trouver a et k. Ainsi, on peut constater qu'un point n'est pas attribué à un paramètre spécifique en particulier, comme on aurait pu le penser avec nos points originaux et la façon dont la démarche a été présentée ;)

En résumé, pour résoudre ce genre de numéro, insère les coordonnées des deux points dans l'équation, puis simplifie ces équations (résous la partie entière). Si un des paramètres est éliminé en cours de route avec une multiplication par 0 comme dans ce cas-ci, alors tant mieux, le calcul sera simplement plus rapide :D Sinon, tu dois utiliser les méthodes de résolution des systèmes d'équations.

En ce qui concerne ta seconde question, on cherche g(14), c'est-à-dire la coordonnée en y du point à x=14. Écrire g(14) dans l'équation ici :

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

signifie simplement qu'on cherche l'image du point à x=14. On aurait aussi pu écrire (bien que cette notation soit moins privilégiée) :

$$y=-2[-\frac{1}{3}(x-5)]+10$$

et résoudre pour trouver y, qui correspond à g(14), l'image du point à x=14.

En résumé, pour n'importe quelle type de fonction, lorsqu'on cherche l'image d'un point, on remplace x dans f(x) par la coordonnée en x de ce point, mais cela n'affecte pas les calculs, on aurait aussi pu écrire \(y\).

J'espère que c'est plus clair pour toi! :)

Salut!

Tu n'as rien fait de mal, ta démarche est excellente! :D

Tu as ceci :

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Il te reste à calculer -(31/42)²+3, ce qui va effectivement de donner un nombre positif.

Si tu as d'autres questions, n'hésite pas à nous réécrire! :)