Secondary V • 1yr.
Bonjour,
J'auarais version d'aide pour ce numéro. Il faut calculer la hauteur de l'image du drain. Par contre, je ne sais pas quoi faire. Aussi, ils me Disney d'utiliser Les propriétés des triangles rectangles
Merci beaucoup et bonne journée!






Explanation verified by Alloprof
This Explanation was verified by a member of the Alloprof team.
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
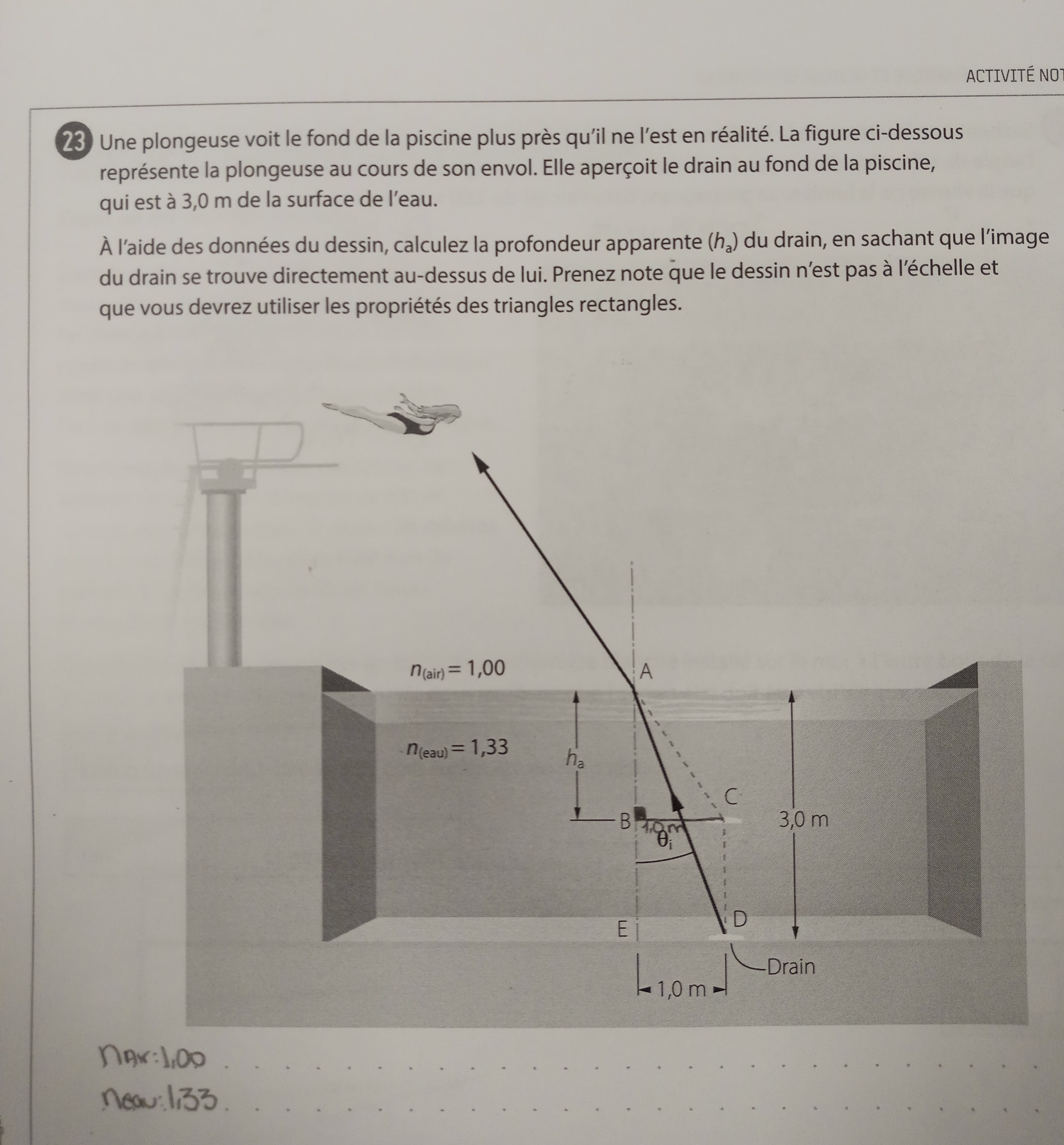
On à le passage du rayon lumineux de l'eau à l'air.
Le rayon s'accompagne d'une réfraction d'angle r par rapport à la normale
Neau sin(θ)=Nair sin(r)
sin(r) =(Neau/Nair ) sin(θ)
sin(r)=(1.33/1) sin(θ)
θ aussi a déterminer
Dans le triangle rectangle AED on a tan(θ)=10/30
coté opposé sur cote adjacent
tan(θ)=0.333
avec la machine à calculer on obtient θ=18.45°
On revient à notre formule
sin(r)=(1.33/1) sin(θ)
sin(r)=(1.33/1) sin(18.45°)
sin(r)=0.42 , machine a calculer r=24.87°
Le rayon luminaux émergeant de la surface de l'eau semble provenir du point C (image virtuelle de D) et se propager en ligne droite.
dans le triangle ABC
tan(r)=mBC/mAB
mAB=mBC/tan(r) mAB=Ha
Ha=10/tan(24.87°)
Ha=21.6 m
Donc la piscine semble moins profonde.