Populaires
Re : Question
Bonjour RubisRouge5076 !😊
Pour étudier en vue de ton examen de demain, concentre-toi sur les idées principales :
- Relis tes notes et souligne les mots-clés importants (culture, langue, lois, armée, routes, etc.).
- Fais un petit résumé avec les éléments essentiels.
- Explique la matière à voix haute dans tes propres mots.
Tu peux aussi effectuer cette révision sur la romanisation :
Bonne étude et bon examen demain ! 💪
Re : Question
Salut!
On te dit que son salaire horaire initial est de 18,50$, et qu'elle a une augmentation de 6%.
Donc, tu dois calculer le 6% de 18,50$ pour trouver de combien son salaire horaire augmente, puis tu devras additionner cette augmentation à 18,50$ pour déterminer son salaire horaire final après l'augmentation (ou tu peux simplement calculer le 106% de 18,50$, ce qui te donnera directement le salaire horaire final après augmentation).
Pour calculer le pourcentage d'un nombre, tu dois multiplier les deux nombres. Voici un exemple, on veut calculer le 28% de 50 :
$$ 0,28 \times 50 = 14$$
Tu peux également utiliser une proportion, comme ceci :
$$ \frac{28}{100}=\frac{?}{50} $$
Puis effectuer un produit croisé :
$$ 28 \times 50 \div 100 = 14$$
Je t'invite à consulter la fiche suivante pour plus d'exemples : Le « tant pour cent » et le « cent pour cent » | Secondaire | Alloprof
Finalement, pour connaitre le salaire hebdomadaire, tu n'auras qu'à multiplier le salaire horaire par 37,5 heures.
Si tu as d'autres questions, n'hésite pas à nous réécrire! :)
Re : Question
Bonjour RubisRouge5076 !
Voici une révision sur la romanisation :
Bonne pratique !
Re : Question
Bonjour, LoupDynamique8419
Pour une présentation sur un animal ça varie selon l'espèce et l'animal. Mais, en général tu peux parler de sa reproduction par exemple combien de bébé il a, combien de temps il reste avec ces parents, tu peux aussi parler de son espérance de vie ou de fun fact que personne ne sait sur ton animal ça peux toujours être intéressant.
voici quelques idées général:
- Habitat : où l’animal vit (forêt, mer, désert, etc.)
- Alimentation : ce qu'il mange et comment il se nourrit.
- Caractéristiques physiques : Sa taille, sa couleur et ses caractéristiques particulières.
- Comportement : comment il se déplace et s'il vit seul ou en groupe.
- Adaptations : ce qui le rend spécial (griffes, camouflage, vitesse, etc.)
- Rôle dans la nature : pourquoi il est important
- Menaces : ce qui nuit à l'espèce (par exemple, la pollution, la chasse).
- Faits intéressants : anecdotes, records et faits surprenants
Passe une bonne soirée,
Question
Est ce que c’est possible d’être accepter en science nature dans un cegep fort du genre bois de Boulogne avec une moyenne pas très haute, comme 75% de moyenne général?
Re : Question
Pour le P, c'est les parentese. tu dois calculer le P en premier. Apres, c'est le E pour exposant comme si j'ai un deux puis en haut j'ai un petite deux tu dois faire 2x2. Pour le M et D c'est multiplication et division. Le premier que tu voit c'est le premier que tu dois calculer. Et le A et S c'est addition et soustraction. le premier que tu voit tu doit le calculer.
Bonne journnée!
Question
Je m'en vais au secondaire c'est quoi le passage du primaire au secondaire car je suis stresser.En plus,je suis deja inscri a une ecole
Re : Question
Salut C3POBeta7641,
Merci d'avoir pris le temps de nous écrire aujourd'hui, surtout en cette semaine de la persévérance scolaire, et j'espère que tu vas bien.
Voici la réponse que mon collègue Louis-Philippe a donné à une question similaire (référence : https://www.alloprof.qc.ca/zonedentraide/discussion/2515 ).
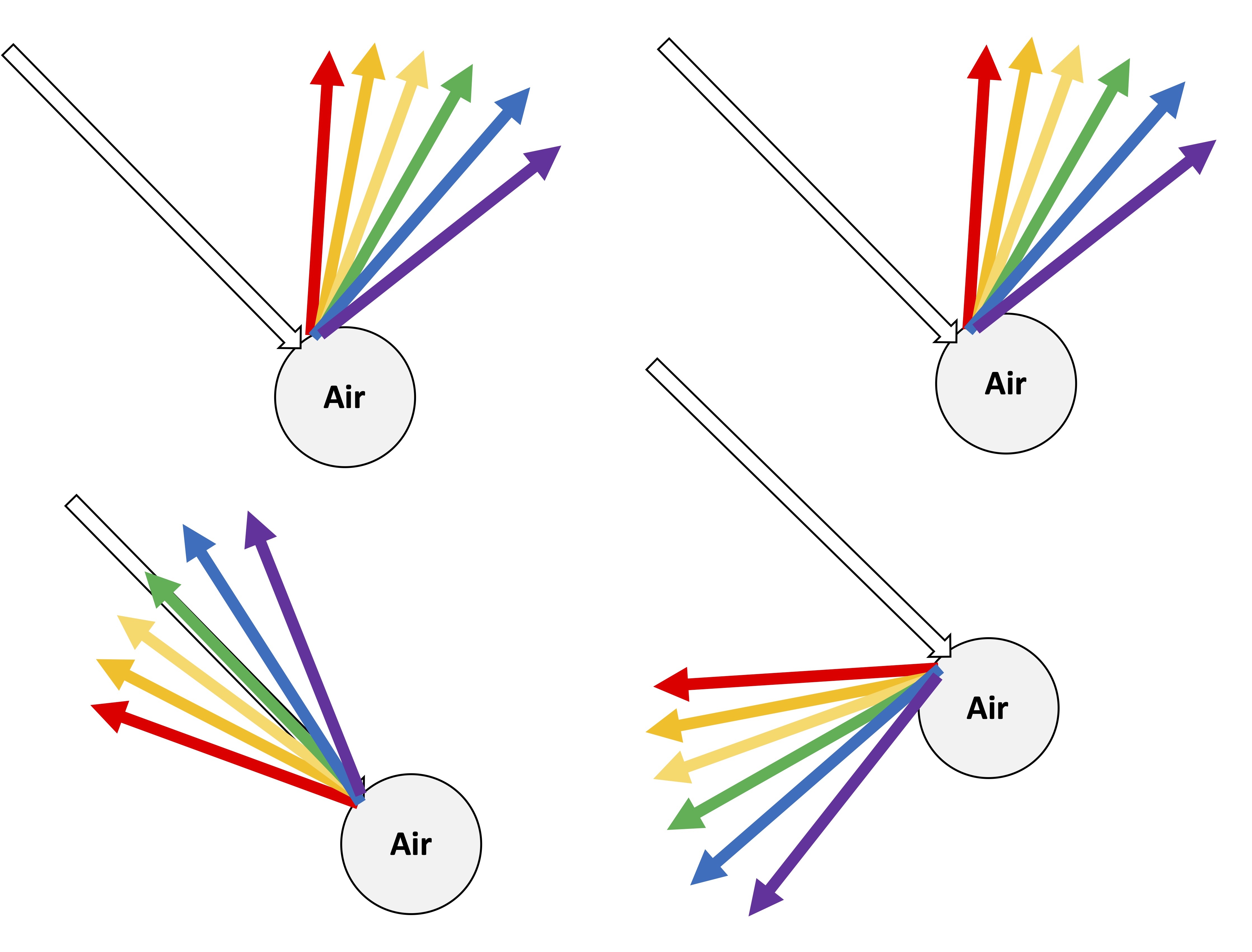
<< Essentiellement, la couleur bleue du ciel a lieu à cause d'un phénomène appelé diffusion : Les particules de lumière (les photons) arrivent dans la couche d'air de la Terre (l'atmosphère) se heurtent contre les particules d'air.
Lorsque cette lumière frappe les particules d'air, elle rebondit dans toutes les directions. C'est à ce moment que le ciel prend sa coloration bleue : Tu savais peut-être déjà que la lumière blanche du Soleil est en réalité composée de toutes les couleurs de l'arc-en-ciel.
Toutes ces couleurs ne sont pas également déviées. En effet, le bleu, l'indigo et le violent sont beaucoup plus déviés que les autres couleurs. Le bleu est aussi plus facilement perceptible par les yeux des humains.
Ainsi, c'est pourquoi on perçoit le ciel comme étant bleu : le bleu est plus dévié et plus facilement perceptible par l'être humain.
Ce vidéo explique la couleur bleue du ciel d'une manière plus technique, mais plus visuelle : https://www.youtube.com/watch?v=fwiEcPCXLcI .>>
En espérant que le tout te soit utile, merci encore et n'hésite pas à nous réécrire au besoin :) !