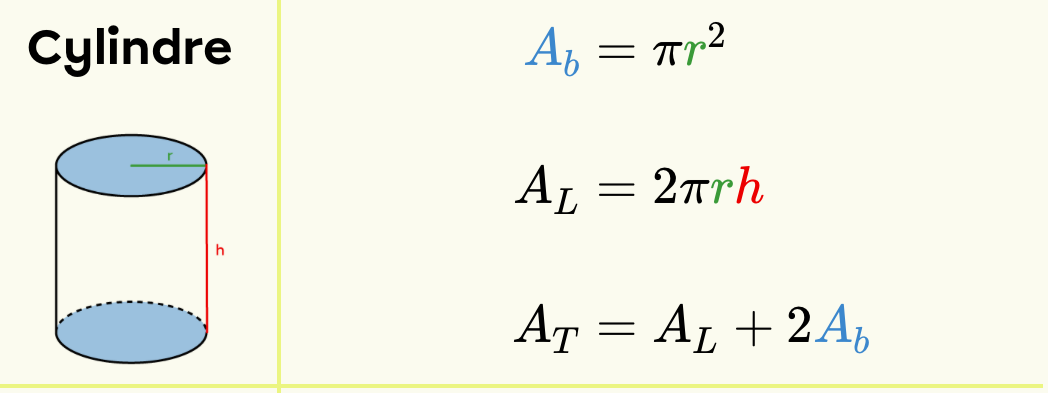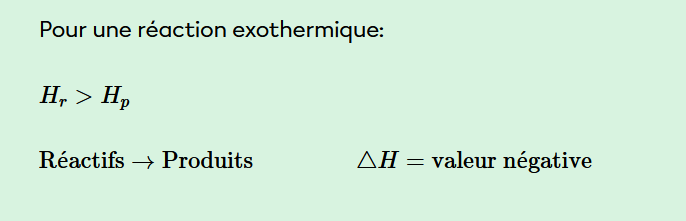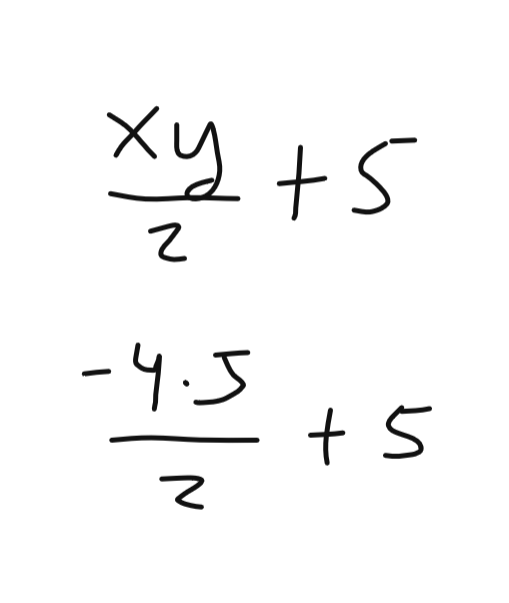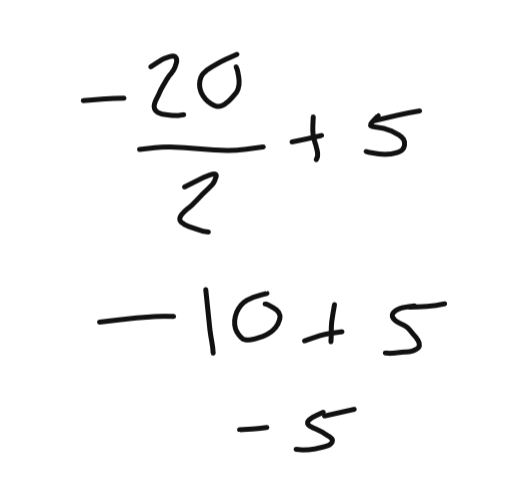Populaires

Salut!

Tu dois utiliser la formule d’aire totale d’un cylindre :

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Nous avons donc l’équation :

$$A_{T}=2\pi r h + 2(\pi r^2) $$

Nous savons que le rayon est de 5 cm et que l'aire totale est de 1020π cm². Nous pouvons alors insérer ces données dans notre équation :

$$1020 \pi=2\pi \times 5 \times h + 2(\pi 5^2) $$

Il ne te reste plus qu’à résoudre l’équation pour trouver la valeur de la variable h, la hauteur du cylindre. Consulte cette fiche au besoin : Les méthodes générales de résolution d'équations | Secondaire | Alloprof

J’espère que c’est plus clair pour toi! :)

Salut!

Avant de poser les restrictions, tu dois factoriser les dénominateurs et le numérateur de la seconde fraction. Ainsi, on doit diviser les expressions \(y²+5y\), \(y²+2y-15\) et \(y²-7y+12\).

On factorise le premier dénominateur en effectuant une mise en évidence simple :

$$y²+5y = y(y+5)$$

On factorise le dénominateur et le dénominateur de la seconde fraction en utilisant la technique du produit-somme :

$$y²+2y-15=(y+5)(y-3)$$

$$y²-7y+12 = (y-3)(y-4)$$

Notre division de fractions rationnelles :

$$ \frac{y^2-3y-4}{y^2+5y} \div\frac{y^2-7y+12}{y^2+2y-15} $$

devient alors :

$$ \frac{y^2-3y-4}{y(y+5)} \div\frac{(y-3)(y-4)}{(y+5)(y-3)} $$

Ensuite, on peut maintenant poser nos restrictions. Pour cela, il faut trouver les valeurs de y qui font en sorte que les dénominateurs soient de 0.

$$ y(y+5) = 0$$

Nous avons deux restrictions pour ce dénominateur : \(y = 0\) et \(y = -5\)

On refait la même chose pour le dénominateur de la seconde fraction :

$$ (y+5)(y-3)=0 $$

Nous avons deux restrictions pour ce dénominateur : \(y = -5\) et \(y = 3\).

Si nous avions eu une addition, une soustraction ou une multiplication, nos restrictions seraient complètes. Or, puisqu'on a une division, cela signifie que nous allons inverser le numérateur et le dénominateur de la seconde fraction et transformer la division en multiplication, comme ceci :

$$ \frac{y^2-3y-4}{y(y+5)} \times \frac{(y+5)(y-3)}{(y-3)(y-4)} $$

Nous devons donc vérifier la valeur de y qui fait en sorte que ce nouveau dénominateur soit nul.

$$ (y-3)(y-4) =0$$

Nous avons deux restrictions pour ce dénominateur : \(y = 3\) et \(y = 4\).

Voilà! Nous pouvons maintenant rassembler toutes les restrictions trouvées, soit y=-5, 0, 3 et 4.

Voici une fiche sur cette notion qui présente plusieurs exemples similaires : La division de fractions rationnelles | Secondaire | Alloprof

Si tu as d'autres questions, n'hésite pas à nous réécrire! :)

Salut :D

Voici les étapes de résolution.

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Il faut d'abord remplacer les variables x et y par les valeurs données, soit (-4) et (5).

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Ensuite, on respecte les priorités des opérations.

Entre chaque variable, il y a une multiplication invisible.

N'hésite pas si tu as d'autres questions :D À bientôt :)