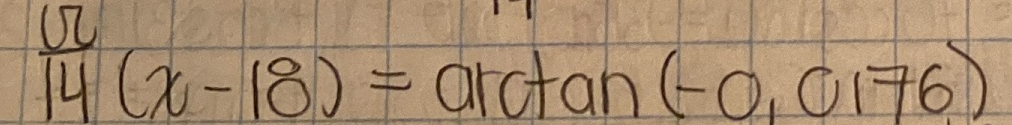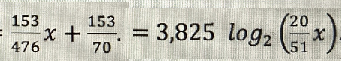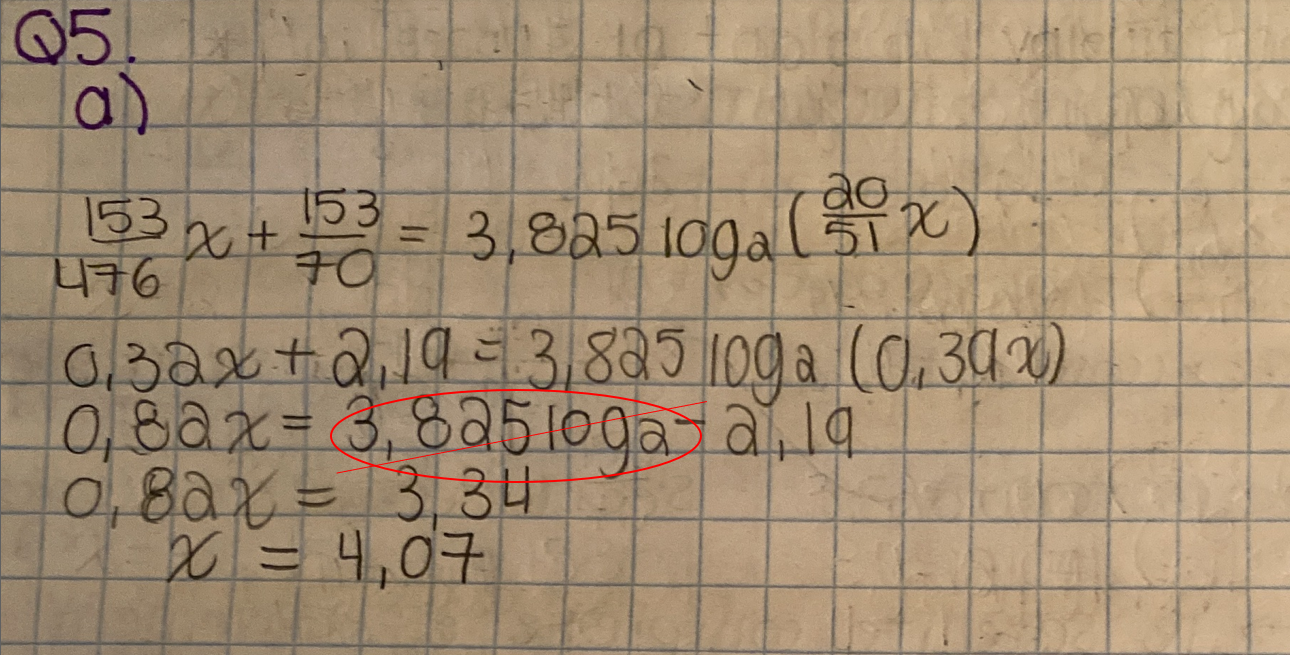Populaires
Re : Question
Bonsoir NickelTurbo,
Merci de faire appel à nos services! :)
En fait, pour aller au secondaire à Brébeuf, il faut remplir certaines conditions. Je te laisse y jeter un coup d'oeil juste ici :
Tu peux te préparer à l'examen d'admission en consultant notre fiche à ce sujet:
Les écoles, notamment l'école Brébeuf, reçoivent énormément d’inscriptions et ont un nombre limité de places pour les nouveaux élèves (ici 252). Il peut parfois arriver que certains élèves soient refusés.
Si tu reçois un refus, ça ne veut pas dire que tu n’es pas un bon ou une bonne élève. Ça veut simplement dire qu’il te reste des choses à travailler. Tu peux demander à l’école d’avoir accès à tes résultats, réviser pendant ta première secondaire et essayer de repasser l’examen d’admission en deuxième secondaire.
Reviens-nous si tu as d'autres questions et bonne préparation! :)
Marilee
Re : Question
Salut!
Tu peux commencer par simplifier la grosse fraction comme ceci :
$$ \frac{2}{3}\div\frac{-5}{7} \div 3\frac{2}{9} $$
Puis, n'oublie pas que lorsqu'on divise par une fraction, c'est l'équivalent de multiplier par l'inverse de cette fraction. On obtient donc ceci :
$$ \frac{2}{3}\times\frac{-7}{5} \div 3\frac{2}{9} $$
On effectue ensuite la multiplication :
$$ \frac{2\times-7}{3\times5} \div 3\frac{2}{9} $$
$$ \frac{-14}{15} \div 3\frac{2}{9} $$
Tu peux suivre le même principe pour la seconde division. Cependant, tu devras d'abord transformer le nombre fractionnaire en fraction. Voici une fiche sur cette notion qui pourrait t'être utile : De la fraction au nombre fractionnaire et l'inverse | Secondaire | Alloprof
Si tu as d'autres questions, n'hésite pas à nous réécrire! :)
Re : Question
Salut !
Elle est catégorisé comme énergie rayonnante, car il s'agi de la provenance. Donc, oui, l'énergie solaire peut être catégoriser dans les énergies rayonnantes.
Si tu as d'autres questions, n'hésite pas !
Re : Question
Ce n'est vraiment pas une question de secondaire IV.
La réponse devrait être 876.42 (sous toute réserve car je n'ai pas fait ce type de calculs depuis longtemps) essentiellement parce que le premier terme (la sommation de 1 à l'infini) est nul.
Note qu'avec le -1 exposant n il y a oscillation du positif au négatif de la somme et avec n de plus en plus grand les divers termes tendent vers zéro.
Re : Question
b)
Tu avais bien commencé puis il y a eu erreur de calcul
(Pi/14)(x-18)=arctg(-0.0176)
(x-18)=(14/Pi) arctg(-0.0176)
x-18=(14/Pi) (-1.008)
x-18=-4.487
x=18-4.487
x=13.513
Re : Question
Bonsoir OursTenace2267,
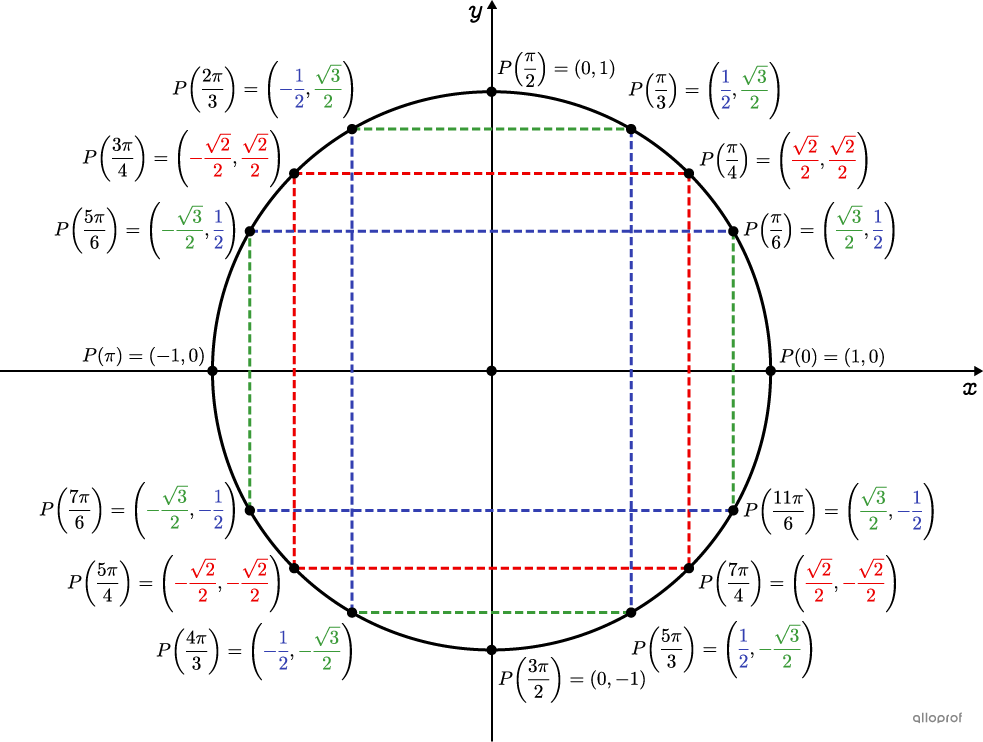
Tu as bien compris comment trouver la règle d'une fonction tangente. Cependant, tu as oublié de changer ta calculatrice en radians. En effet, tan(pi/4)=1. Rappelle-toi aussi du cercle trigonométrique sachant que tanx=cosx/sinx. Poursuis le reste de tes calculs.
N'hésite pas à nous recontacter si tu as d'autres questions!
Re : Question
Pour rechercher le point de départ et le point de rencontre tu dois résoudre l'équation
que tu as bien commencé puis il y a eu des erreurs en cours de route
(puisque ils ont donné 3.825 à trois décimales après la virgule tu devrais arrondir à 3 décimales après la virgule).
ca donne
0.321 x +2.186 = 3.825 (log2 (0.392 x))
On convertit avec la regèle le log du produit en somme
log(ab)=log(a)+log(b)
log2(0.392 x)=log2(0.392)+log2(x)
Puis on calcule log2(0.392) par la machine à calculer on change la base 2 du log parce que les machines à calculer calculent le log en base 10
log2(0.392)=log10(0.392)/log10(2)
mais pour tout A positif on a log10(A)=log(A)
log(A) c'est l'opération que tu réalises avec la machine à calculer
log2(0.392)=log(0.392)/log(2) ici c'est le log c'est le log de la calculatrice
log2(0.392)=-0.407/0.301
log2(0.392)=-1.352
log2(0.392 x)=log2(0.392)+log2(x)
log2(0.392 x)=-1.352+log2(x)
l'équation devient:
0.321x+2.186=3.825(-1.352+log2(x))
0.321x+2.186=3.825(-1.352)+3.285 log2(x)
0.321x+2.186=3.825(-1.352)+3.285 log2(x)
0.321x+2.186=-5.171+3.285 log2(x)
0.321x+2.186+5.171=3.285 log2(x)
0.321x+7.357=3.285 log2(x) équation a résoudre
sauf qu'au programme on n'as pas étudié des équations du type
ax+b=c log(x)
Comme l'énoncé avait suggéré de faire un tableau de valeurs et comparer les deux expressions y1 et y2
On revient à la forme des coordonnes y1 et y2
y1=0.321 x +2.186
y2=3.825 (log2 (0.392 x))
Selon le graphique le point de départ se situe proche de 5, on va calculer pour des valeurs de x autour de 5
On remplace x par 5 dans y1 et y2
y1=0.321 5 +2.186 ____________________ y1=3.791
y2=3.825 (log2 (1.960)) ,
y2=3.825(log(1.960))/(1og(2))___________ y2=3.714
On prend x=5.1
y1=0.321 5.1 +2.186_____________________y1=3.823
y2=3.825 (log2 (1.999)) ,
y2=3.825(log(1.999))/(1og(2))____________y2=3.825
y1 proche de y2
On peut prendre comme solution x =5.1
le site de décollage à pour coordonnées (5.1 , 3.825)
on voit bien sur la figure que l'ordonnée est proche de 4
Détermination du point de rencontre
Selon la figure x est proche de 41
x=41
y1=0.321 41 +2.186___________________y1=15.347
y2=3.825 (log2 (0.392 41))_____________y2=15.327
x=40.9____________________________y1=15.315
_________________________________y2=15.315
le largage du satellite se fera au point de coordonnées (40.9 , 15.315)
c'est cohérent avec la figure présentée
Re : Question
Bonsoir OursTenace2267,
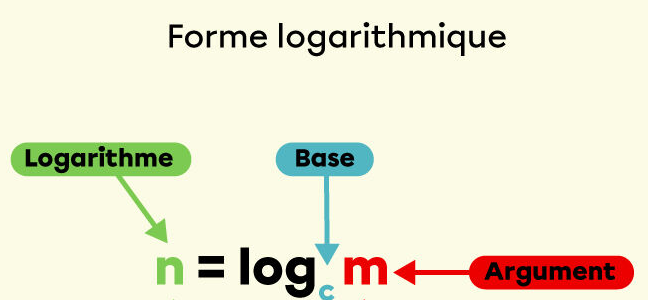
Lorsque tu es en forme logarithmique, il doit toujours y avoir un argument.
Ainsi, tu n'as pas le droit de l'annuler comme s'il ne représentait qu'une simple multiplication et laisser le log vide. Tu dois donc recommencer ton calcul. De plus, je te conseille de ne pas arrondir tout de suite.
N'hésite pas à nous recontacter si tu as d'autres questions!
Re : Question
il faut lire continuellement des livres en Français, tu peux choisir n'importe quel thème, si tu as des préférences par exemple, l'histoire les sciences la culture générale, la politique etc. , alors donnes toi a fond et arrêtes l'usage d'internet et le téléphone et surtout le Français des textos et TikTok
Re : Question
Bonjour!
La différence entre un polygone et un polyèdre, c'est que l'un est une forme en 2 dimensions (polygone) et l'autre est un solide, donc à 3 dimensions (polyèdre)! :D
Je t'invite à consulter les fiches ci-dessous pour en savoir plus :
Les polygones
Les polyèdres
Si tu as d'autres questions, n'hésite pas à nous réécrire. Nous te répondrons avec plaisir!
Laurie :)