Populaires

Salut!

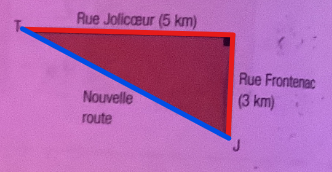
Tu dois d'abord calculer la longueur de chaque chemin :

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Le chemin initial (en rouge) est de 5 km + 3 km = 8 km.

Pour trouver la longueur du nouveau chemin (en bleu), on peut utiliser le théorème de Pythagore, puisqu'on a un triangle rectangle. Posons x comme étant la longueur en km de la nouvelle route. Ainsi, on aurait ceci :

$$ x^2 = 5^2 + 3^2 $$

$$ x^2 = 25 + 9 $$

$$ x^2 = 34$$

$$ \sqrt{x^2} = \sqrt{34}$$

$$ x = 5.83$$

On trouve alors que la nouvelle route a une longueur de 5,83 km.

Puis, on nous dit qu'elle roule à une vitesse de 45 km/h. On peut alors trouver le temps requis pour traverser une distance de 8 km (ancienne route) et de 5,83 km (nouvelle route) en posant une proportion.

On peut tout de suite remarquer que le trajet durera moins d'une heure. Donc, pour simplifier nos calculs, transformons la vitesse en km/min :

$$ \frac{45\ \text{km}}{60\ \text{min}} = \frac{8\ \text{km}}{?\ \text{h}} $$

On effectue un produit croisé :

$$ ? = 8 \times 60 \div 45 = 10,67\ \text{min} $$

Le premier trajet dure 10,67 minutes.

Effectuons le même calcul pour le nouveau trajet :

$$ \frac{45\ \text{km}}{60\ \text{min}} = \frac{5,83\ \text{km}}{?\ \text{h}} $$

On effectue un produit croisé :

$$ ? = 5,83 \times 60 \div 45 = 7.77\ \text{min} $$

Le nouveau trajet dure 7,77 minutes.

On peut maintenant calculer la différence pour trouver le temps économisé grâce à la nouvelle route :

$$ 10,67\ \text{min} - 7,77\ \text{min} = 2,9\ \text{min} $$

Voilà! On trouve donc qu'elle a gagné 2,9 min, ou encore 2 min et 54 secondes.

Si tu as d'autres questions, on est là! :)