Populaires
Re : Question
Merci pour ta question!
(et merci d'avoir inclut une image du problème à nouveau; cela nous aide à répondre à ta question!)
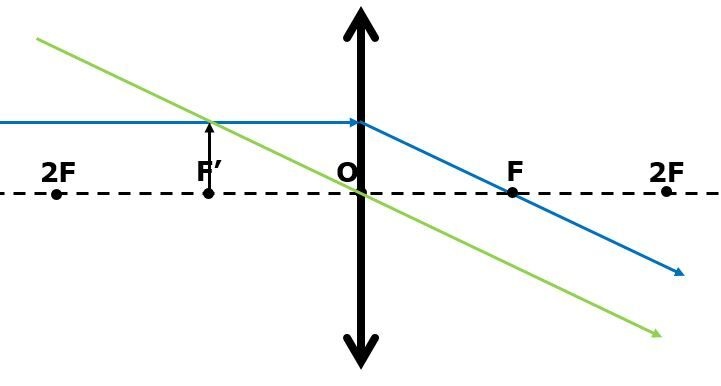
Je te suggère de mesurer ces distances en sachant le comportement des images par rapport aux lentilles auxquelles tu auras accès. Par exemple :
Si tu places l'objet directement sur le foyer d'une lentille convergente, il n'y aura pas d'image. Ainsi, tu peux déplacer l'objet jusqu'à ce qu'il n'y ait plus d'image. Tu sauras que cette position correspond au foyer de la lentille, ce qui devrait te permettre de mesurer sa position grâce à une règle.
Cela dit, à mon avis, ces données de longueur focale seront fournies au laboratoire. Tu n'auras qu'à assembler les lentilles ensemble et t'assurer que ton choix de lentilles maximise le grossissement tous en respectant les contraintes énoncées dans le document.
Cette fiche du site d'Alloprof explique les images formées par les lentilles convergentes :
J'espère que cela t'aide.
N'hésite pas si tu as d'autres questions!
Re : Question
Salut!
Tu as bien commencé en posant x comme étant le nombre de tournesols à 8 pétales.
Si on en a 3 fois plus à 13 pétales, on a donc 3x tournesols à 13 pétales.
On a donc jusqu'à maintenant :
x : nombre de tournesols à 8 pétales
3x : nombre de tournesols à 13 pétales
Pour les tournesols à 21 pétales, on a 7 de plus que la moitié de la somme du nombre de tournesols à 8 et à 13 pétales. Je te laisse trouver l'expression algébrique correspondant au nombre de tournesols à 21 pétales.
Une fois que tu auras ton nombre de tournesols de chaque type, sachant que le nombre total de pétales est de 592, tu pourras poser l'équation suivante :
nombre total de pétales =
8 × nombre de tournesols à 8 pétales +
13 × nombres de tournesols à 13 pétales +
21 × nombre de tournesols à 21 pétales
et la résoudre pour trouver l'inconnu.
Si tu as d'autres questions, n'hésite pas à nous réécrire! :)
Re : Question
Merci pour ta question!
Pour ce qui est de la tâche, avec quelle partie spécifique as-tu de la difficulté? N'hésite pas à poser une question à nouveau en précisant quelle partie te pose difficulté.
L'équation des lunetiers peut probablement t'aider à trouver la longueur focale (lf) :
$$ \frac{1}{d_i}+\frac{1}{d_o}=\frac{1}{f} $$
Légende :
• di : distance image-miroir
• do : distance objet-miroir
• f : longueur focale
Sinon, cette équation sur le grossissement (G) devrait t'aider :
$$ G=\frac {h_{i}}{h_{o}} = \frac {-d_{i}}{d_{o}} = \frac {-l_{f}}{l_{o}} = \frac {-l_{i}}{l_{f}} $$
Légende :
• G : grossissement
• hi : hauteur de l'image
• ho : hauteur de l'objet
• di : distance entre l'image et le miroir
• do : distance entre l'objet et le miroir
• li : distance entre l'image et le foyer principal
• lo : distance entre l'objet et le foyer secondaire
• lf : longueur focale
Note : tu n'as pas besoin de connaitre toutes ces valeurs; seulement hi et ho; di et do; lf et lo; ou li et lo te permettront de trouver G.
Cette fiche du site d'Alloprof explique les équations des lentilles :
N'hésite pas si tu as d'autres questions!
Re : Question
Salut!
Oui exactement, c'est la même chose, ce sont simplement deux façons de nommer la fonction! :)
Re : Question
Salut!
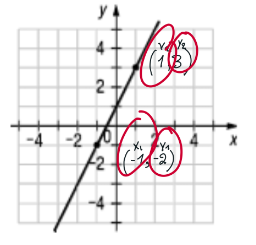
Ton erreur est ici :
Tu as mal identifié les coordonnées du point du 3e quadrant, le point est à y=-1 et non y=-2. Les bonnes coordonnées sont donc (-1,-1).
Le reste de ta démarche est excellent, donc en corrigeant cela, tu obtiendras la bonne règle!
Bonne soirée :)
Re : Question
Salut !
S'agit-il de l'exercice sur la fonction périodique ? Si c'est le cas, alors il te faut gérer les valeurs en fonction de sa position dans le cycle. Un exemple de comment faire se trouve dans cette fiche :
Tu trouve le cycle qui concorde avec ta valeur de \(x\). Par la suite, tu utilises la valeur de \(x\) restante pour extrapoler la valeur de \(f(x)\).
Je te laisse essayer par toi-même et si tu as d'autres questions, n'hésite pas !
Re : Question
Salut !
C'est une matière un peu trop avancé pour le secondaire 2, mais il s'agit d'un exercice qui te demande de résoudre un système d'équation.
Tout d'abord, tu dois déterminer tes inconnus. Il s'agit simplement de \(x\) le nombre d'humains et \(y\) le nombre de chiens. Tu dois par la suite traduire les énoncés correctement :
Pour le nombre de pattes, tu sais qu'un être humain en a deux (\(2x\) pour le total de pattes d'humain) et qu'un chien en a quatre (\(4y\)). De plus, chacun a une seule tête (\(x+y=21\).
Je te laisse essayer par toi-même et si tu as d'autres questions, n'hésite pas !
Re : Question
Merci pour ta question!
En fait, les cellules sont 4n au début de la mitose, et se séparent en deux cellules filles 2n à la fin. Ainsi, les chromatides qui se séparent durant l'anaphase sont des chromatides 4n qui se séparent en chromatides 2n. Voilà pourquoi elles sont toujours «doubles».
Cette fiche du site d'Alloprof explique les phases de la mitose en détail :
N'hésite pas si tu as d'autres questions!
Re : Question
Bonjour PoutineIntergalactique9812,
Merci d'avoir utilisé la zone d'entraide pour répondre à tes questions. Je vais pouvoir t'aider !
D'abord, voici trois liens qui expliquent clairement l'anaphase et la méiose :
- https://www.alloprof.qc.ca/fr/eleves/bv/sciences/les-etapes-de-la-mitose-notions-avancees-s1530
- https://www.alloprof.qc.ca/fr/eleves/bv/sciences/la-division-cellulaire-s1320
- https://www.alloprof.qc.ca/fr/eleves/bv/sciences/les-etapes-de-la-meiose-notions-avancees-s1531
J'espère que cela répond à ta question, n'hésites pas à contacter à nouveau !
Ne lâche pas !
QuartzLogique9766
Re : Question
Merci pour ta question!
Peu importe la situation, une constante mathématique infiniment juste n'a pas d'incertitude. Cependant, les règles habituelles pour trouver les incertitudes s'appliquent toujours.
Par exemple, la formule pour trouver la circonférence d'un cercle est π fois le diamètre :
$$ c= π•d $$
π n'a pas d'incertitude, mais imaginons que le diamètre a une incertitude de 30±2 u.
$$ c = π•30 $$
Pour trouver l'incertitude résultante, il faut trouver l'incertitude relative (il s'agit d'une multiplication) :
$$ ∆c = (\frac{∆d}{d})•c = \frac{2}{30}•(30•π) = 2π ≈ ± 6 $$
Ainsi, la mesure finale est la suivante :
$$ c = (94±6)\:u $$
Cette fiche du site d'Alloprof explique l'incertitude et les calculs d'incertitude :
N'hésite pas si tu as d'autres questions!