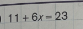Populaires
Re : Question
Salut!
On te demande de trouver la variable dépendante et la variable indépendante du problème. Ce sont ces variables qui forment le problème lorsqu’elles sont mises en relation. Le troisième point de l’énoncé te donne ces variables.
La dernière section de cette fiche pourrait t'être utile : Les types de variables | Secondaire | Alloprof
Si tu as d’autres questions, reviens nous voir! :)
Re : Question
Salut!
Consulte les deux explications suivantes :
- comment identifier si une solution est saturée ou non? — Alloprof
- c'est quoi une solution non saturée — Alloprof
Et reviens nous voir si tu as d'autres questions! :)
Re : Question
Salut!
Un dénominateur ne peut jamais être égal à 0. Ainsi, tu dois calculer la valeur de x qui fait en sorte que le dénominateur sera 0, ce sera ta restriction! En d'autres mots, tu résous ceci :
expression au dénominateur contenant la variable x ≠ 0
Voici un exemple :
$$ \frac{2x+3}{7x-2} $$
On calcule ceci :
$$7x-2≠0$$
$$7x≠2$$
La restriction est donc :
$$x≠\frac{2}{7}$$
J’espère que c’est plus clair pour toi! :)
Re : Question
Salut !
Voici une source qui pourrait t'être utile :
Cependant, Alloprof ne fournit pas d'exercice et le mieux reste d'aller voir ton enseignant pour des exercices supplémentaires !
Si tu as d'autres questions, n'hésite pas !
Re : Question
Bonjour PlatineComique7339,
Merci d'avoir utilisé la zone d'entraide pour répondre à tes questions !
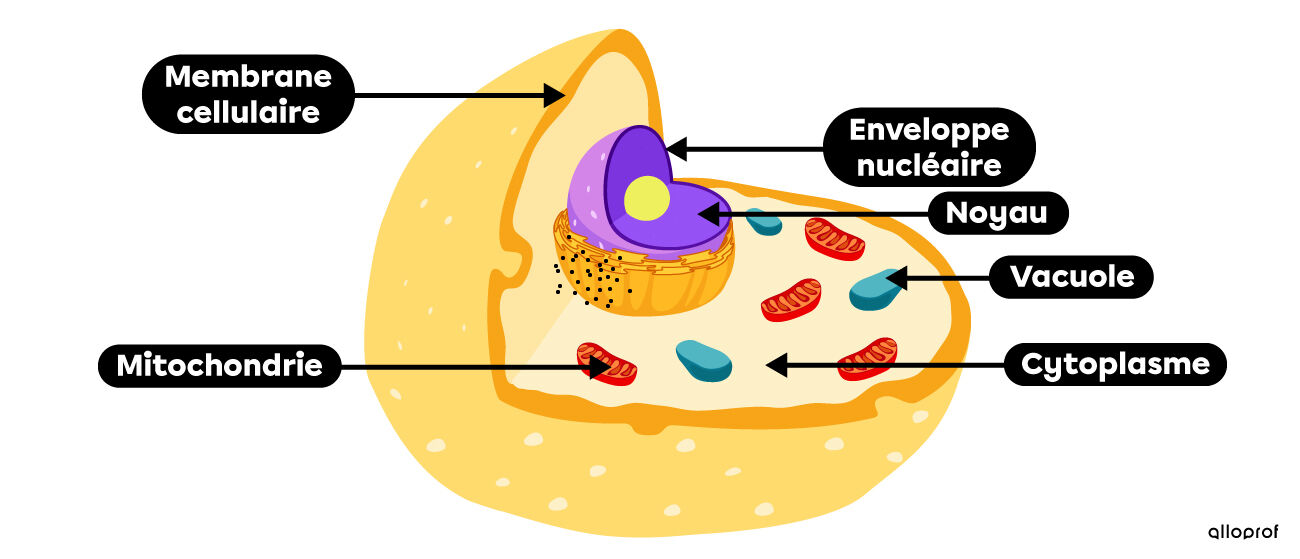
Tout d'abord, la plus grande différence entre les deux se situe dans leur composition respective, mais également dans le rôle que chacune joue dans l'organisme et à quel type d'être vivant elles appartiennent (animaux ou végétaux).
Voici un schéma de la cellule animale :
Voici maintenant un schéma de la cellule végétale, essaie d'observer les principales différences :
Pour davantage d'informations sur le rôle de chaque type de cellules et sur leurs parties respectives, tu peux consulter cette fiche d'Alloprof :
N'hésite pas à nous réécrire si tu as d'autres questions, ça nous fera plaisir de te répondre :D
Bon travail,
SaturneTenace1401
Re : Question
Bonjour PlatineComique7339,
Merci d'avoir utilisé la zone d'entraide pour répondre à tes questions.
D'abord, je pense que cette fiche Alloprof pourrait être un bon début pour te donner plus d'informations sur les cellules végétales et animales.
Ensuite, la cellule végétale est une cellule qui est à la base de tous les organismes végétaux. Une cellule animale est un type de cellule eucaryote à partir de laquelle sont composés les différents tissus animaux.) À mon avis, la chose la plus importante à savoir est que la cellule végétale se distingue de la cellule animale par 3 caractéristiques :
1)Elle possède une paroi cellulosique, une membrane extérieure rigide faite de cellulose.
2)Elle possède une seule grande vacuole servant à entreposer des substances et permettant la croissance de la cellule en y emmagasinant l’eau par un phénomène d’osmose.
3)Elle possède des chloroplastes qui contiennent la chlorophylle, un pigment à l’origine de la couleur verte des végétaux et qui participe au processus de photosynthèse.
Si tu connais les trois caractéristiques, tu pourrais mieux les différencier:)
J'espère que cela répond à ta question,
Bonne étude,
FlamantRose2573
Re : Question
Salut!
On sait que le périmètre d'un rectangle se trouve comme ceci :
$$ périmètre = 2\times longueur+2\times largeur$$
Puisque le périmètre est de 80 mètres, on a alors l'équation suivante :
$$ 80 = 2\times longueur+2\times largeur$$
De plus, je pense que tu as mal retranscrit l'énoncé, et on te dit que "la longueur du terrain mesure 2 m de moins que le double de sa largeur"
Ainsi, on peut traduire cela en l'équation suivante :
$$ longueur = 2\times largeur - 2 $$
Tu peux alors insérer cette équation dans notre équation du périmètre :
$$ 80 = 2\times longueur+2\times largeur$$
devient :
$$ 80 = 2\times (2\times largeur - 2 )+2\times largeur$$
Remplaçons la variable largeur par x :
$$ 80 = 2\times (2\times x - 2 )+2\times x$$
$$ 80 = 2(2x - 2 )+2x$$
Il ne reste plus qu'à résoudre cette équation pour pouvoir trouver la valeur de x, donc la largeur du terrain! Connaissant la largeur, tu pourras ensuite déduire la longueur. Je te laisse terminer.
Si tu as d'autres questions, n'hésite pas à nous réécrire! :)
Re : Question
Salut!
Tu as effectué la méthode de la balance sans t'en rendre compte! ;)
La réponse est bien x=5, mais attention, écrire 2x=10/2 est une erreur.
Tu ne peux jamais effectuer une opération sur un côté de l'équation et pas sur l'autre aussi. Ce que tu fais sur un côté, tu es obligé de la faire sur l'autre côté aussi, sinon l'équation n'est plus équilibrée, la balance penchera d'un côté plus que de l'autre.
Ainsi, puisque tu avais 2x=10, tu dois écrire 2x/2=10/2, ou encore x = 10/2, si tu souhaites montrer la division, et non 2x=10/2.
La méthode de la balance est très facile à utiliser lorsqu'on la comprend bien, elle est systématique et tu peux l'appliquer à n'importe quelle équation. Je te conseille donc de la pratiquer et de ne pas essayer de résoudre l'équation d'une autre façon.
En appliquant la méthode de la balance plus explicitement, voici ce que tu as fait :
Pour résoudre, 2x+12=22, on va d'abord déplacer le 12 de l'autre côté, en effectuant l'opération inverse, comme ceci :
$$ 2x + 12 - 12 = 22-12$$
$$ 2x = 22-12$$
$$ 2x = 10$$
Puis, on va éliminer le coefficient en effectuant l'opération inverse d'une multiplication :
$$ \frac{2x}{2}=\frac{10}{2}$$
$$ x = 5 $$
Si tu as d'autres questions, n'hésite pas à nous réécrire! :)
Re : Question
Salut!
Pas ne panique! Regardons ça ensemble!
Lorsqu'on te demande de résoudre une équation, on te demande ainsi de trouver la valeur de la variable inconnue de l'équation. Par exemple, ici, on veut trouver la valeur de x :
Pour résoudre une équation, on peut avoir recours à différentes méthodes, l'une d'entre elles est la méthode de la balance.
Résolvant cette équation ensemble avec cette méthode. On a :
$$ 11 + 6x = 23$$
Tout d'abord, il est important de comprendre les différentes parties d'une équation. Lorsqu'on a un terme sans variables (sans lettre), comme 11 et 23 dans cet exemple, on a alors ce qu'on appelle des termes constants, ou encore des constantes. On peut additionner les constantes d'une équation.
Lorsqu'on a plusieurs termes composés des mêmes variables affectés des mêmes exposants, on a des termes semblables. Par exemple, 18x et 3x pourraient être des termes semblables. 32x et 24y ne sont pas des termes semblables, puisqu'il ne possède pas la même variable.
Lorsqu'on a des termes semblables, on peut les additionner en additionnant leur coefficient. Par exemple, 3x+2x=5x.
Pour résoudre une équation, notre but est donc de rassembler les constantes ensembles et les termes semblables ensemble. Puis, nous allons vouloir avoir d'un côté de l'équation un terme avec une variable, et de l'autre, une constante.
Pour revenir à notre exemple, on aimerait rassembler les constantes 11 et 23. Pour ce faire, on va déplacer la constante 11 de l'autre côté de l'équation. Pour la déplacer, on effectue l'opération inverse. L'opération inverse d'une addition est une soustraction. Donc, en soustrayant 11 de chaque côté de l'équation, on déplace ainsi la constante de l'autre côté :
$$ 11 + 6x - 11 = 23 - 11$$
$$ 6x = 23 - 11$$
$$ 6x = 12$$
N'oublie pas que chaque fois que tu effectues une opération d'un côté de l'équation, tu dois aussi l'effectuer de l'autre côté! Il serait faux de soustraire 11 d'un côté seulement et pas de l'autre.
Ensuite, on a maintenant une constante d'un côté et un terme ayant une variable de l'autre. Notre dernière étape est d'éliminer le coefficient de la variable, soit le 6. Pour ce faire, nous allons effectuer l'opération inverse d'une multiplication, soit une division :
$$ \frac{6x}{6} = \frac{12}{6}$$
$$ x = \frac{12}{6}=12 \div 6 = 2$$
Et voilà! Voici une fiche sur cette notion pour plus d'exemples de résolution d'équations : Les méthodes générales de résolution d'équations | Secondaire | Alloprof
J'espère que c'est plus clair pour toi! Reviens nous voir si ce n'est pas le cas ;)