Secondaire 5 • 11m
Bonsoir,
pour clarifier cette questions: https://www.alloprof.qc.ca/zonedentraide/discussion/117428/question/p1
en fait, je voulais savoir comment passer d'une forme:
à la forme:
Voici un exemple de règle que je veux simplifier: 1/2log3(4(x-6)) + 5
Concrètement, on enlève pas nécessairement le a et le k, mais je cherche une façon de les intégrer dans ma formule de base.
Merci pour votre aide!
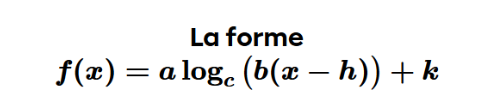







Explication d'Alloprof
Cette explication a été donnée par un membre de l'équipe d'Alloprof.
Bonjour,
Pour effectuer la transformation demandé, tu dois utilisé les propriétés des logarithmes :
\( a \cdot \log_c(b(x-h)) + k = \)
\(\log_c\left( (b(x-h))^a \right) + k = \)
\(\log_c\left( (b(x-h))^a \right) + k \cdot \log_c(c) = \)
Il est à noter ici que puisque \( \log_c(c) = 1, k * \log_c(c) = k*1 = k\).
\(\log_c\left( (b(x-h))^a \right) + \log_c(c^k) = \)
\(\log_c\left( (b(x-h))^a \cdot c^k \right) = \)
\(\log_c\left( b^a \cdot (x-h)^a \cdot c^k \right) = \)
\(\log_c\left( (b^a \cdot c^k) \cdot (x-h)^a \right) = \)
\(\log_c\left( B(x-h)^a \right) \)
où \(B = b^a \cdot c^k\)
Si tu as d'autres questions n'hésite pas à venir les poser !
Bonne journée :)
Suggestions en lien avec la question
Suggestion en lien avec la question
Voici ce qui a été trouvé automatiquement sur le site, en espérant que ça t’aide!