Bonjour!
J'avais quelques confusions sur les lois de Newton; les-voici:
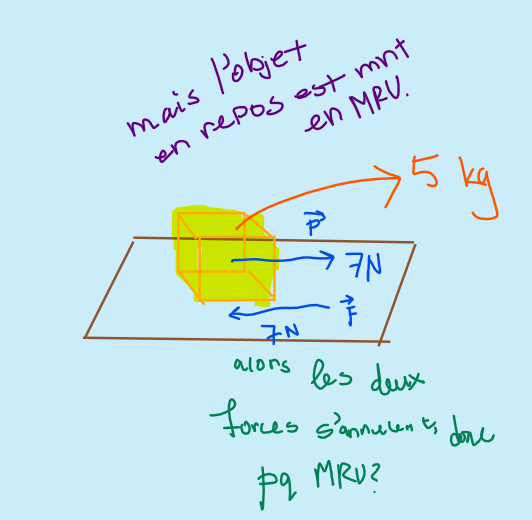
1) Voici un scénario de MRU qui me mélange tout le temps. Supposons que nous avons une masse de 5kg (initialement en repos) posé sur la table et que je le pousse avec une force constante de 7N vers la droite. Lorsqu'on trace le DCL, je ne comprends pas pourquoi dans mon corrigé, la force la norme du force de frottement de la boîte avec la surface de la table sera aussi égale à 7N pour que l'objet soit en MRU. En fait, si la force de ma poussée est de la même norme que la force de frottement, alors les deux vecteurs s'annuleront, non? Et, si les deux vecteurs s'annulent, alors pourquoi mon objet bougerait à une vitesse constante lorsque ma main continue d'être en contact avec la masse, dont la friction annule ma possée?
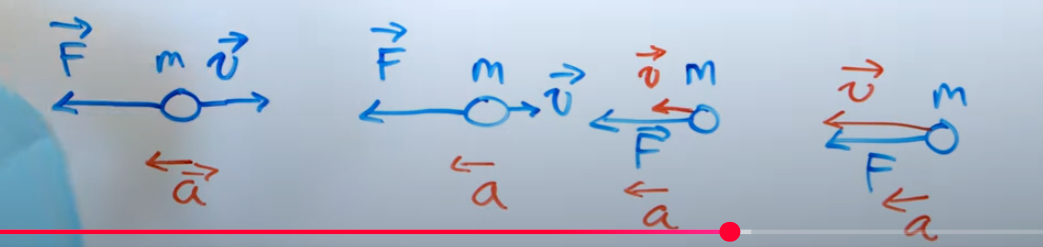
2) Sur le schéma ci-contre, je ne comprends pas une chose sur la décélération de l'objet. Supposons que j'ai une balle dans l'espace (sans friction) et qu'elle a déjà une vitesse intiale constante de 3m/s. Sur cet objet en MRU, je continue d'appliquer une force de 4N dans la direction opposée. Je ne comprends pas pourquoi, dans le schéma ci-contre, l'objet va continuer de décélérer vers la droite, puis sa vitesse devient nulle, avant d'augmenter sa vitesse vers la gauche. Je ne comprends pas qu'est-ce qui se passe avec la direction de la force, de l'accélération et de la vitesse en fonction du temps.
Si jamais la capture d'écran est un peu flou, alors voici la source: https://youtu.be/5T_O6Zt5Xt4?t=1192
J’aimerais vraiment avoir l’explication de mme Katia kaci, car quand c’est vous qui expliquez, tout devient clair pour moi en quelques secondes! Ce n'est pas grave si vous n'êtes pas disponible aujourd'hui, mais je veux clarifier mes doutes, pourriez-vous m'aider s.v.p ?
Merci beaucoup :D






Explication d'Alloprof
Cette explication a été donnée par un membre de l'équipe d'Alloprof.
Salut!
Regardons tout cela de plus près :D
Concernant ta première question, tu as tout à fait raison, si la force de la poussée est de la même norme que la force de frottement, alors les deux vecteurs s'annuleront.
Cependant, une somme des forces nulle ne veut pas dire que l’objet est immobile, ça veut dire qu’il n’accélère pas, donc la vitesse est constante, c'est pourquoi on a un MRU et non un MRUA.
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Reprenons l'équation de la deuxième loi de Newton pour mieux comprendre :
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Si l'accélération est nulle (a=0), cela signifie que la vitesse est constante. Par exemple, si on pousse avec une vitesse de 1 m/s, alors cette vitesse sera toujours la même, on ne ralentit pas et on n'accélère pas. Si on remplace \(a\) par 0 dans notre équation, on obtient :
$$F_{R}=m\times 0$$
$$F_{R}=0$$
Donc, peu importe la masse, si l'accélération est nulle, c'est-à-dire si on pousse à une vitesse constante, la force résultante sera nulle. Cela ne veut pas dire qu'il n'y a aucune force appliquée à l'objet, mais plutôt que les différentes forces appliquées s'annulent pour avoir une somme de 0 au final.
$$F_{R}=P-F_{f}=7-7=0$$
En résumé, pour que l'objet soit en MRU, il faut que la vitesse soit constante, donc il faut que l'accélération soit nulle, donc il faut avoir une force résultante nulle, donc la force de frottement doit être égale à la force de poussée, puisqu'elles sont de sens opposé et donc s'annuleront! :D
Si la force de frottement était différente de la force de poussée, cela signifierait que la force résultante (la somme des deux forces) ne serait pas de 0. Par exemple, si la force de frottement était de 6 N, on aurait une force résultante de 1 N appliquée sur l'objet :
$$F_{R}=P-F_{f}=7-6=1$$
Donc, ce ne serait pas un MRU, mais plutôt un MRUA, puisqu'on aurait une petite accélération!
$$F_{R}=ma$$
$$1=5\times a$$
$$\frac{1}{5}= a$$
De plus, si l’objet était initialement déjà en mouvement quand les deux forces s’équilibrent, il va continuer à bouger à cette même vitesse constante, car rien ne vient changer cette vitesse (c’est la première loi de Newton, la loi de l’inertie).
Là où ça peut devenir mélangeant, c’est lorsqu'on part d’un état de repos. Pour qu’un objet immobile se mette à bouger, il faudrait au début qu’il y ait une force résultante non nulle pour lui donner une accélération et ainsi changer sa vitesse de v=0 m/s à v=1 m/s par exemple. Mais, si dès le départ la force de frottement est exactement égale à ta poussée, il restera immobile (v=0 et a=0, donc v reste à 0).
C’est pour ça qu’en pratique, au moment où tu commences à pousser, il y a souvent une petite période d’accélération où la poussée est plus grande que le frottement jusqu’à ce que l’objet atteigne une vitesse constante. Une fois cette vitesse constante atteinte, les deux forces s’équilibrent et on entre en MRU.
Ensuite, concernant ta seconde question, la balle se déplace dans l’espace à une vitesse initiale constante de 3 m/s vers la droite (donc MRU car vitesse constante → a=0), et on applique ensuite une force constante de 4 N vers la gauche (donc dans le sens opposé à la vitesse).
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Puisqu'il n'y a aucune autre force appliquée sur l'objet, la force résultante sera de 4 N vers la gauche.
À ce moment-là, tu t'attendrais à ce que l'objet se dirige alors vers la gauche, n'est-ce pas (puisque tu as une balle qui va vers la droite, tu la tires vers la gauche, et il n'y a aucune résistance car on est dans l'espace, donc elle devrait aller logiquement dans le sens de ta poussée)? Donc, la vitesse, qui était de v= 3 m/s (positive donc vers la droite), devrait changer pour devenir v= -3 m/s (négative donc vers la gauche) (ou un autre nombre, l'important c'est que la vitesse devienne négative pour aller vers la gauche), tu es d'accord? En d'autres mots, on veut passer de v=3 à v=-3, on a donc besoin d'un a non nul pour faire ce changement de vitesse!
On a besoin d'une décélération (diminution de vitesse) pour passer de v=3 à v=0. La variable \(a\) sera négative pour être de signe opposé à la vitesse qui est positive (si l'accélération est de signe opposé à la vitesse alors on a une décélération). De plus, on a besoin d'une accélération (augmentation de vitesse) pour passer de v=0 à v=-3. La variable \(a\) sera aussi négative ici, car on veut être de même signe que la vitesse qui est maintenant négative.
Petit résumé pour t'aider :
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Cette vidéo sur le sujet pourrait t'aider : Les signes de la vitesse et de l'accélération (Physique XXI Tome A Section 1.5) - YouTube
En d'autres mots, pour passer de v=3 à v=-3, on décélère pour changer de sens et atteindre v=0, la balle s'arrête momentanément donc v=0, puis on accélère pour atteindre v=-1, v=-2, puis v=-3 etc.
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Tant que la force de poussée sera appliquée, il y aura une force résultante non nulle, et donc une accélération. Si on arrête d'appliquer la poussée à un moment donné, l'accélération deviendra nulle et la vitesse sera constante et égale à celle au moment où la poussée a été arrêtée.
Pour mieux comprendre, tu peux t'imaginer le superhéros Hulk essayer de tirer une corde vers la gauche reliée à une voiture en mouvement vers la droite. Puisque la voiture est lourde, il aura de la difficulté à faire changer de direction le mouvement de la voiture. Au début, il tire, la voiture se met à ralentir progressivement mais est toujours en mouvement vers la droite (donc v positif) (on peut s'imaginer Hulk détruire le sol avec ces pieds à ce moment-là tellement il tire fort), puis la voiture se met enfin à aller vers la gauche grâce à la poussée de Hulk et il se met à courir (donc v négatif). Lors du petit moment de transition où la voiture passe d'un mouvement vers la droite à un mouvement vers la gauche, la vitesse est nulle.
C'est un peu la même chose pour le cas de cette balle dans l'espace!
Voilà! J'espère que c'est plus clair pour toi! Reviens nous voir si tu n'es pas sûr de comprendre quelque chose! :)
Suggestions en lien avec la question
Suggestion en lien avec la question
Voici ce qui a été trouvé automatiquement sur le site, en espérant que ça t’aide!