Zone d’entraide

ParulineOptimiste7031

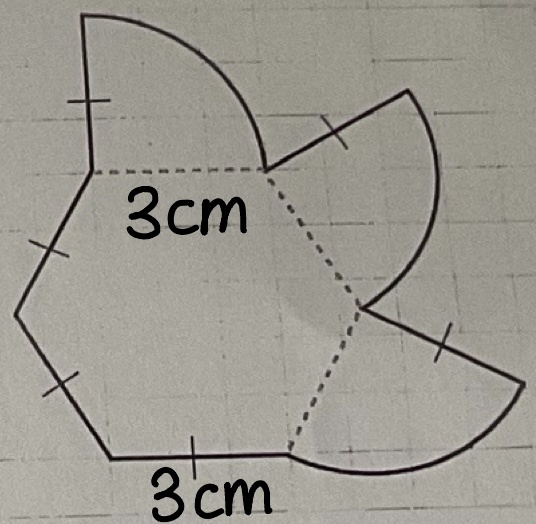
Le but est de déterminer l’aire de cette figure, mais il faut que je sache exactement où est l’apothème de l’hexagone et je ne sais pas comment on peut trouver l’apothème d’un polygone régulier.

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Katia K

Salut!

Comme expliqué par FerUpsilon5520, un hexagone possède des triangles équilatéraux. Tu peux donc utiliser le théorème de Pythagore pour trouver l'apothème de l'hexagone, qui est aussi une des cathètes du triangle rectangle dont l'hypoténuse est de 3 cm et dont l'autre cathète est de 1,5 cm (puisqu'il s'agit de la moitié de la mesure du côté).

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

N'hésite pas à nous réécrire si tu as d'autres questions! :)

FerUpsilon5520

• Pour l'apothème d'un polygone régulier

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

• Pour cet hexagone tu as donc 6 triangles dont la base est de 3 cm et la hauteur est l'apothème a.
• Note que l'hexagone a la particularité que ses triangles sont équilatéraux.
• L'aire de l'hexagone est donc 6 x aire d'un triangle de base 3 et de hauteur a. Tu trouves a grâce au théorème de Pythagore
• Tu connais l'aire d'un disque : c'est π(rayon)², ici c'est 3/4 d'un disque que l'on a, et le rayon du disque est de 3 cm
• Pour plus d'information, va voir https://www.alloprof.qc.ca/fr/eleves/bv/mathematiques/le-perimetre-et-l-aire-des-polygones-reguliers-m1197