Matières
Niveaux
Le théorème de Pythagore
Fiche | Mathématiques
Le théorème de Pythagore, aussi appelé relation de Pythagore, est une relation qui permet de trouver la mesure d’un côté d’un triangle rectangle lorsqu’on connait celle des 2 autres côtés.
Secondaire
3
Table des matières
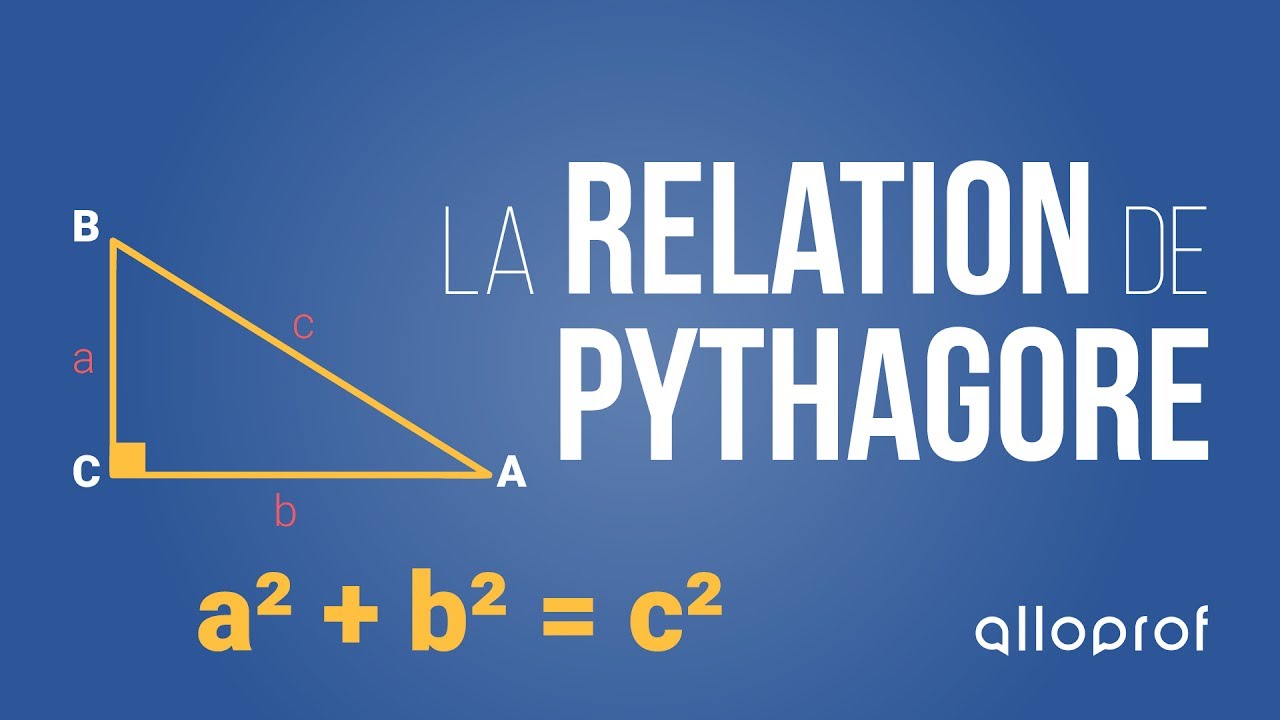
Les cathètes d’un triangle rectangle, souvent notées |a| et |b,| correspondent aux 2 côtés qui forment l’angle droit.
L’hypoténuse d’un triangle rectangle, notée |c,| correspond au côté le plus long. Autrement dit, l’hypoténuse est le côté opposé à l’angle droit.
Le théorème de Pythagore s’énonce de la façon suivante.
Dans un triangle rectangle, la somme du carré des cathètes est égale au carré de l’hypoténuse.||a^2+b^2=c^2||
D’autres lettres que |a,| |b| et |c| peuvent être utilisées pour représenter le théorème de Pythagore. Par exemple, l’équation |x^2+y^2=z^2| est tout aussi valide que l’équation |a^2+b^2=c^2.|
Vidéo
La relation de Pythagore
Exemples
Voici quelques exemples d'application du théorème de Pythagore.
Il est possible d’utiliser la relation de Pythagore pour vérifier si un triangle est rectangle ou non. En effet, un triangle est rectangle si et seulement si la relation de Pythagore est respectée.
-
Si la relation |a^2+b^2=c^2| est vraie, alors le triangle est rectangle.
-
Si la relation |a^2+b^2=c^2| est fausse, alors le triangle n’est pas rectangle.