Secondaire 4 • 3a
Bonjour,
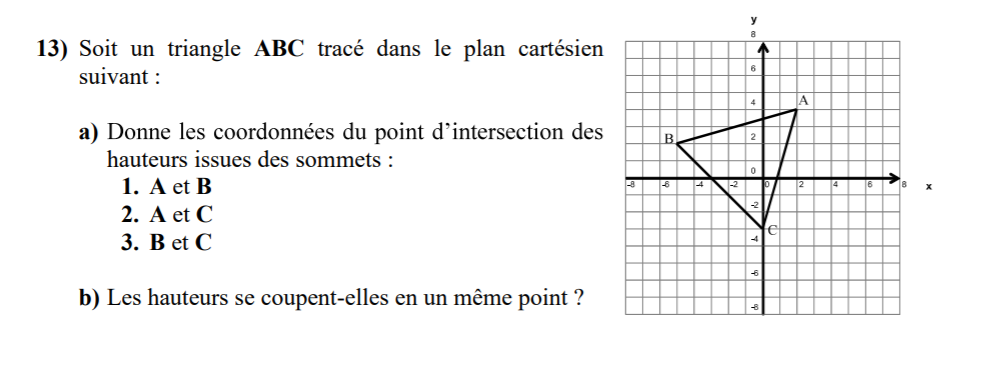
J'ai une question concernant ce numéro.
Que veut-on dire par point d'intersections des hauteurs...
Veut-on savoir l'intersection des hauteurs formés par les sommets A et B, genre doit-on trouver la règle des droites des hauteurs dont le sommet est A et B puis faire un système d'équation pour trouver leur point d'intersection.
Merci et bonne journée! :)






Explication d'Alloprof
Cette explication a été donnée par un membre de l'équipe d'Alloprof.
Salut Angelina,
En effet, on trouve le point d'intersection des hauteurs. Pour cela, tu dois résoudre des systèmes d'équations. Et pour résoudre des systèmes d'équations, on a besoin des équations...
Pour trouver l'équation de la hauteur isssue de \(A\) :
1) Trouve la pente du côté opposé à \(A\), le côté \(BC\).
2) Calcule l'opposé de l'inverse de cette pente puisque la hauteur est perpendiculaire. Rappel : l'opposé de l'inverse de 3/7 est -7/3 (exemple).
3) Trouve l'équation de la hauteur sous la forme \[y = ax + b\] Tu connais sa pente (calculée au #2) et tu connais aussi les coordonnées d'un point par lequel elle passe : le point \(A\).
Refais la même démarche pour trouver les équations des hauteurs issues de \(B\) et de \(C\).
Je ne pense pas trop gâcher la surprise, mais il s'avère que les trois hauteurs se rencontrent en un même point.
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Les solutions aux trois systèmes d'équations devraient donc être les mêmes.
Voilà ! Bon travail !
Salut Angelica!
Je crois que ton raisonnement est correct. Le schéma ci-bas représente cette situation.
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Dans ce cas là, il te faut les coordonnées de l'intersection de la droite ajoutée. Pour ce faire, tu dois connaître l'équation d'une droite passant par les points B et C ainsi que l'équation perpendiculaire à celle-ci passant par A. Une fiche alloprof sur ce sujet pourrait t'aider :
Passe une belle soirée et si tu as d'autres questions, n'hésite pas !
Suggestions en lien avec la question
Suggestion en lien avec la question
Voici ce qui a été trouvé automatiquement sur le site, en espérant que ça t’aide!