Bonsoir,
J'ai fait ce numéro de math, mais je n'arrives pas à la bonne réponse. Pouvez-vous m'expliquer pourquoi.
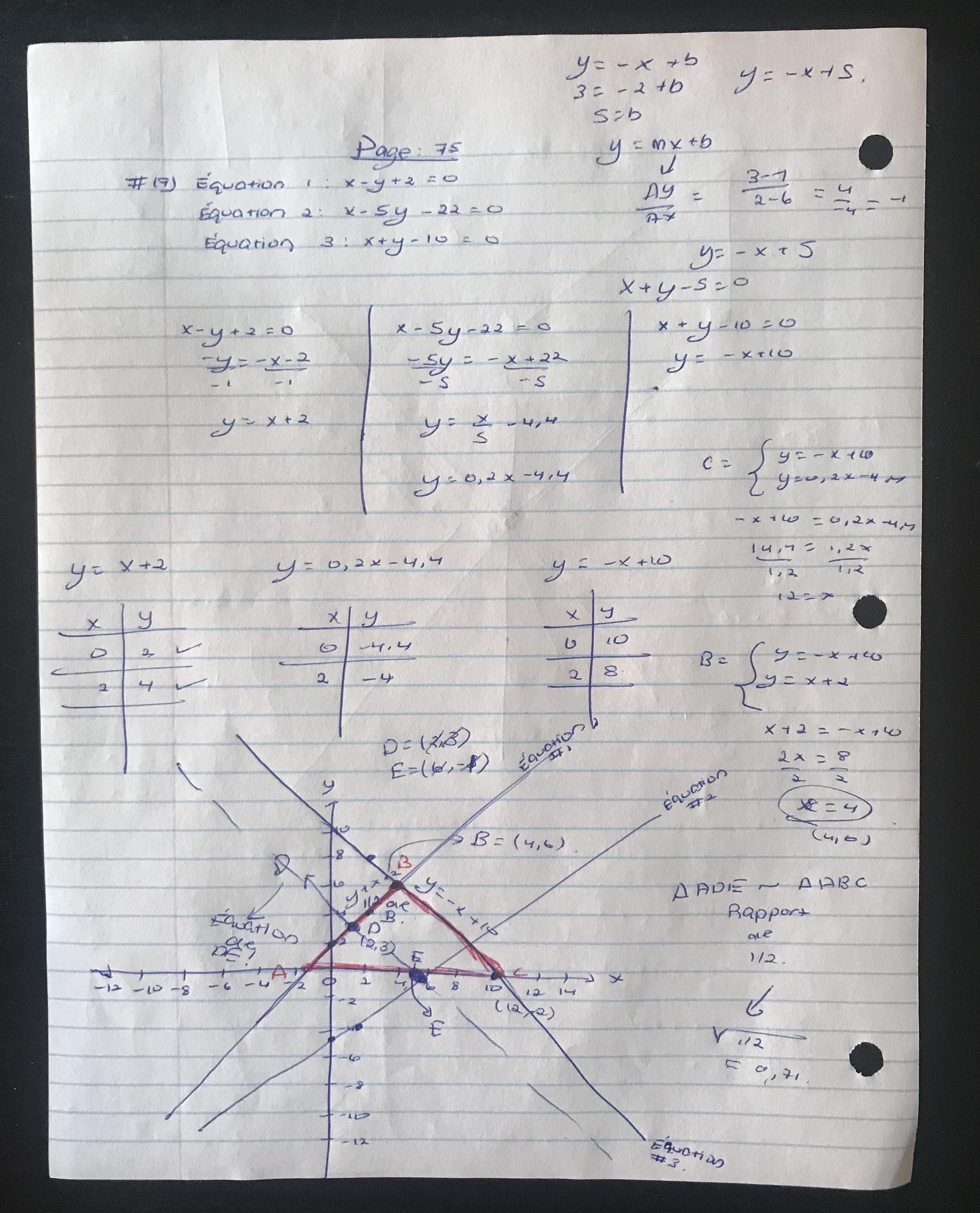
Voici mes étapes
1) J'ai commencé par transformer les 3 équations données sous forme fonctionnelle ce qui m'a donné : Équation 1 --> y = x + 2, Équation 2 --> y = 0,2 x - 4,4 et Équation 3 --> y = - x + 10.
2) J'ai fait une table de valeurs pour tracer un graphique contenant ces 3 équations.
3) J'ai dessiné un triangle dont je ne suis pas trop certaine.
Voici ma démarche. Ma réponse est la suivante : y = -x + 5 et la bonne réponse est la suivante : x + 5y - 10 = 0. (Désolé, pour mes démarches qui sont vraiment en désordre...) Je crois que le problème c'est probablement le dessin de mon triangle, mais je ne suis pas certaine.
Sinon, j'aimerais savoir si je suis quand même sur la bonne voie, car si cette question est dans l'examen de mercredi, il y aurait un peu plus de détails donnés...
Merci et bonne soirée! :)







Explication d'Alloprof
Cette explication a été donnée par un membre de l'équipe d'Alloprof.
Salut AngélinaOrAutonome2754!
Le défi de ce numéro est certainement la définition du triangle semblable au triangle ABC. Le triangle ADE suivant est semblable au triangle ABC:
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Par contre, on ne respecte pas la consigne que le segment \(\overline{DE}\) ne doit pas être parallèle au segment \(\overline{BC}\).
La réponse d'Alain est donc excellente concernant le triangle ADE. En effet, il devrait ressembler à ceci (avec les points A, B, C, D et E):
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
La condition de similitude entre les triangles ABC et ADE est Côté - Angle - Côté (CAC): les côtés proportionnels sont \(\overline{AD}\) et \(\overline{AC}\), ainsi que \(\overline{AE}\) et \(\overline{AB}\). Puisque le point A est commun aux deux triangles, l'angle A est donc identique pour les deux triangles.
Après avoir tracé les triangles à partir des équations et des points D et E, je te suggère les étapes suivantes qui m'ont mené à la réponse du solutionnaire:
1. Trouver les coordonnées du point A. Pour t'aider, tu devrais arriver à A = (4,6).
2. Trouver les coordonnées du point B. J'ai trouvé B = (-8, -6). Fais les calculs de ton côté et vérifie que tu arrives aux mêmes coordonnées que moi.
3. Trouver les coordonnées du point C. J'ai trouvé C = (12, -2). Encore une fois, fais les calculs de ton côté pour comparer avec ma réponse.
4. Trouver la longueur du segment \(\overline{AB}\) à partir des coordonnées des points A et B.
5. Trouver la longueur du segment \(\overline{AC}\) à partir des coordonnées des points A et C.
6. Trouver la longueur du segment \(\overline{AE}\) à partir des informations dans l'énoncé.
7. Trouver la longueur du segment \(\overline{AD}\) encore une fois à partir des informations dans l'énoncé.
8. Trouver les coordonnées du point D à partir de la longueur du segment \(\overline{AD}\) trouvé à l'étape 7 et des coordonnées du point A trouvées à l'étape 1.
9. Trouver les coordonnées du point E à partir de la longueur du segment \(\overline{AE}\) trouvée à l'étape 6 et des coordonnées du point A trouvées à l'étape 1.
10. Il ne te reste qu'à trouver l'équation de la droite qui passe par les points D et E. Utilise les coordonnées trouvées aux étapes 8 et 9.
Voici trois fiches d'AlloProf contenant des notions qui pourraient t'être utiles afin de résoudre le problème:
Je te laisse essayer de faire le problème en entier. Si tu rencontres des difficultés, reviens nous poser des questions dans la zone d'entraide, c'est avec plaisir que je vais t'aider à nouveau! :)
Charles
(4,6) est le point A.
Les points B et C ne sont pas ceux que tu as trouvés.
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Pour que le côté DE ne soit pas parallèle au côté BC, il ne faut pas situer D au milieu de AB ni E au milieu de AC.
Je laisse un prof t'expliquer les détails ...
Suggestions en lien avec la question
Suggestion en lien avec la question
Voici ce qui a été trouvé automatiquement sur le site, en espérant que ça t’aide!