Bonjour,
Je n'arrive à retracer ces deux paraboles dans le graphique:
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
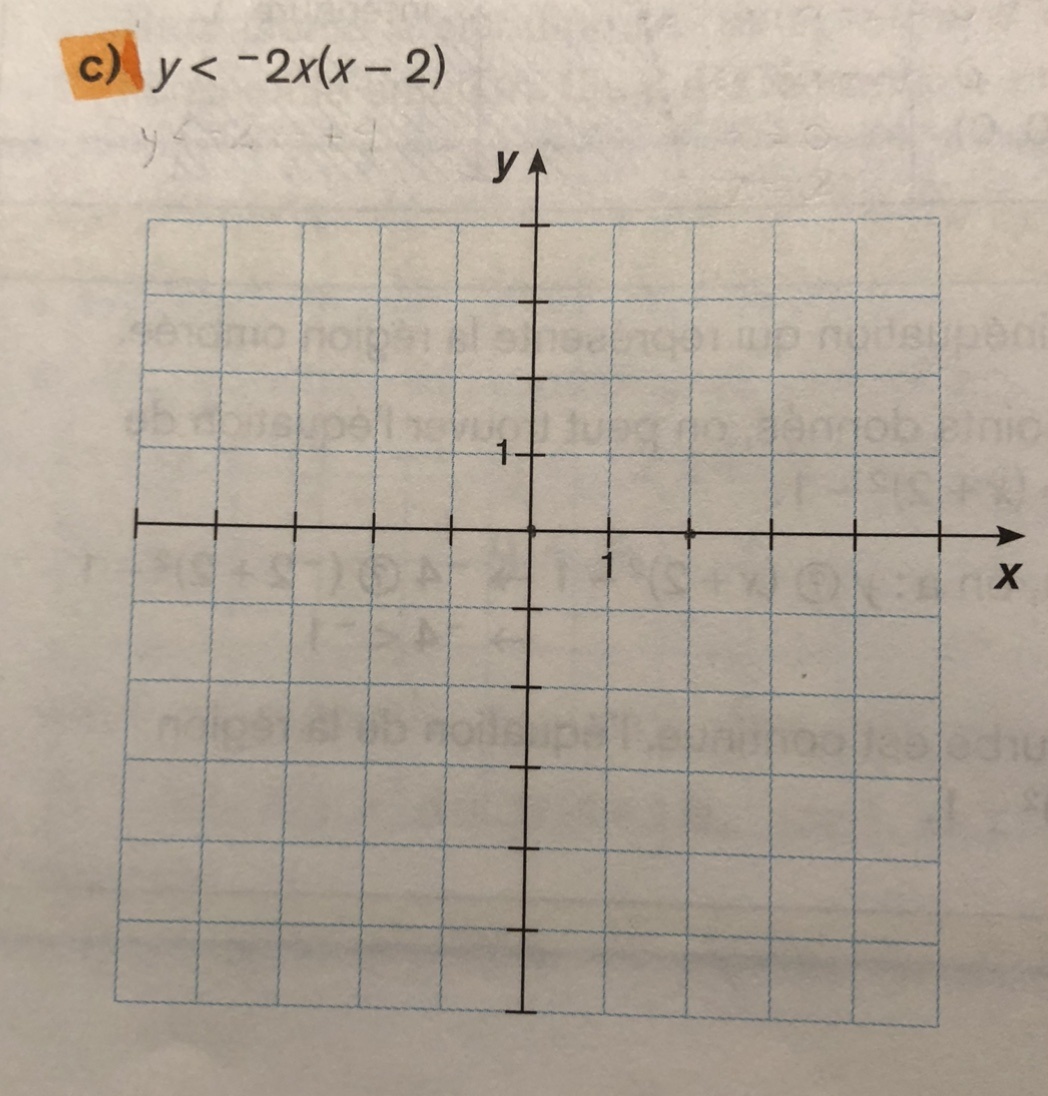
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Ensuite, je ne ne comprends pas ce qu'il faut faire après avoir trouvé la règle dans ce problème ci:
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
La règle que j'ai trouvé est f(x)= -5(x-10)au carré + 600
Puis finalement je n'arrive pas à trouver la règle de ce problème:

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
C'est tout je vous souhaite une bonne soirée et merci d'avance!









Explication d'Alloprof
Cette explication a été donnée par un membre de l'équipe d'Alloprof.
Bonjour,
Commençons par la première partie.
Pour tracer des paraboles tu peux t'aider grâce à la fiche explicative suivante:
Je vais quand même te l'expliquer et te guider.
Règle générale, une fonction polynomiale de degré 2 s'écrit ainsi: \(y = ax^{2} + bx + c\).
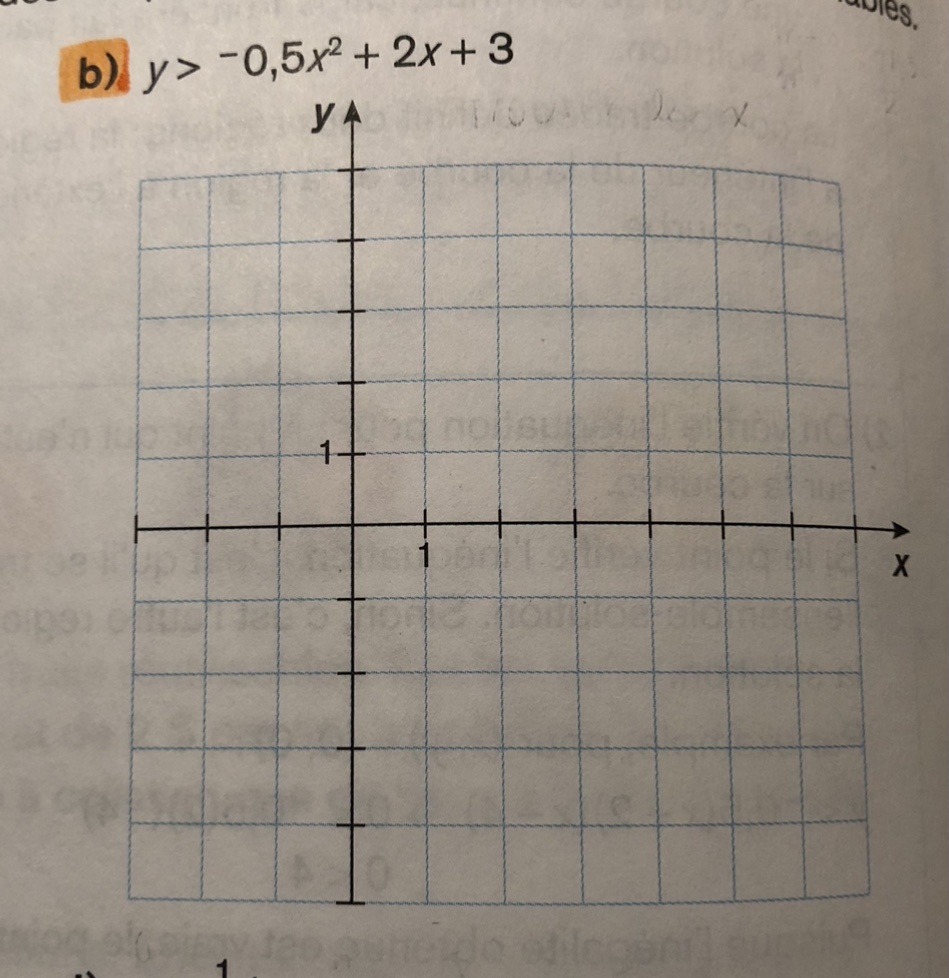
Tu as l'inéquation \(y > -0,5x^{2} + 2x + 3\).
Pour tracer la fonction, on la met sous la forme \(y = -0,5x^{2} + 2x + 3\), où \(a = -0,5\), \(b = 2\) et \(c = 3\).
Voici les prochaines étapes pour tracez le graphique d'une fonction polynomiale de degré 2 :
1) Le sommet \((h,k)\) se calcule de la manière suivante.
$$\begin{align} (h,k) &= \left( - \frac{b}{2a}, \frac{4ac-b^2}{4a}\right) \\ &= \left(- \frac{2}{2 \cdot -0,5}, \frac{4 \cdot -0,5 \cdot 3 - 2^2}{4 \cdot -0,5} \right) \\ &= \left(- \frac{2}{-1}, \frac{-6 - 4}{-2} \right) \\ &= \left( \frac{2}{1}, \frac{-10}{-2} \right) \\ &= \left( 2 , 5 \right) \\ \end{align} $$
2) Les zéros se calculent ainsi.
$$\begin{align} x_{1,2} & =\frac{-b \pm \sqrt{b^2-4ac}}{2a} \\ &= \frac{-2 \pm \sqrt{2^2 - 4 \cdot -0,5 \cdot 3}}{2 \cdot -0,5} \\ &= \frac{-2 \pm \sqrt{4 + 6}}{-1}\\ &= \frac{-2 \pm \sqrt{10}}{-1}\\ &= 2\pm \sqrt{10} \\ \end{align} $$
Pour avoir \(x_1\) et \(x_2\), on utilise dans la formule le - pour l'un, le + pour l'autre.
$$ x_1 = 2 - \sqrt{10} \approx -1,1623 $$
$$ x_2 = 2 + \sqrt{10} \approx 5,1623 $$
On a les deux points \((-1,1623; 0)\) et \((5,1623; 0)\).
3) Puisque \(c = 3\) tel que trouvé plus haut, on a le point d'ordonnée à l'origine \((0, 3)\).
4) Pour trouver le point à la même hauteur que l'ordonnée à l'origine, il faut d'utiliser l'axe de symétrie dont l'équation est \(x = h\), donc \(x = 2\) trouvé en 1).
Puisque le premier point est à x=0 et que l'axe de symétrie est \(x = 2\) (ce qui est le milieu), on sait que l'autre point se trouve donc à 2 unités plus loin, donc à \(x = 4\)!
De ce fait, l'autre point a comme coordonnée \((4, 3)\).
5) On sait aussi que lorsque \(a > 0\), les pattes de la courbe pointent vers le haut, le point le plus bas est le sommet. C'est comme le sourire d'un bonhomme content !! 🙂 Lorsque \(a < 0\), les pattes de la courbe pointent vers le bas, la coordonnée la plus haute est le sommet. Comme la bouche d'un bonhomme triste ☹.
Ici, notre \(a = -0,5 < 0\), donc ça pointe vers le bas!
On peut maintenant mettre les points dans un plan cartésien et tracer la fonction.
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Ta question ne portait que sur le dessin de la parabole, mais si jamais tu voulais aussi de l'aide pour résoudre une inéquation de degré 2 tu peux te fier à la fiche suivante:
Pour ton deuxième exercice, le c), tu n'as qu'à suivre les mêmes étapes.
Il est à noter que lorsque la façon dont l'(in)équation est écrite te pose problème, tu peux toujours la faire passer sous une forme à l'aide de quelques trucs.
Dans ton cas, si tu veux résoudre de la même façon que la question précédente, tu peux faire
$$ y < -2x(x-2) $$
$$ y < -2x^2 + 4x $$
Tu peux maintenant faire les manipulations! Voici la parabole que tu devrais obtenir, à titre de validation.
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Peut-être que le rôle des paramètres dans une fonction polynomiale de degré 2 pourrait t'aider aussi:
Ensuite, passons à la deuxième partie de ta question, c'est-à-dire les deux derniers numéros.
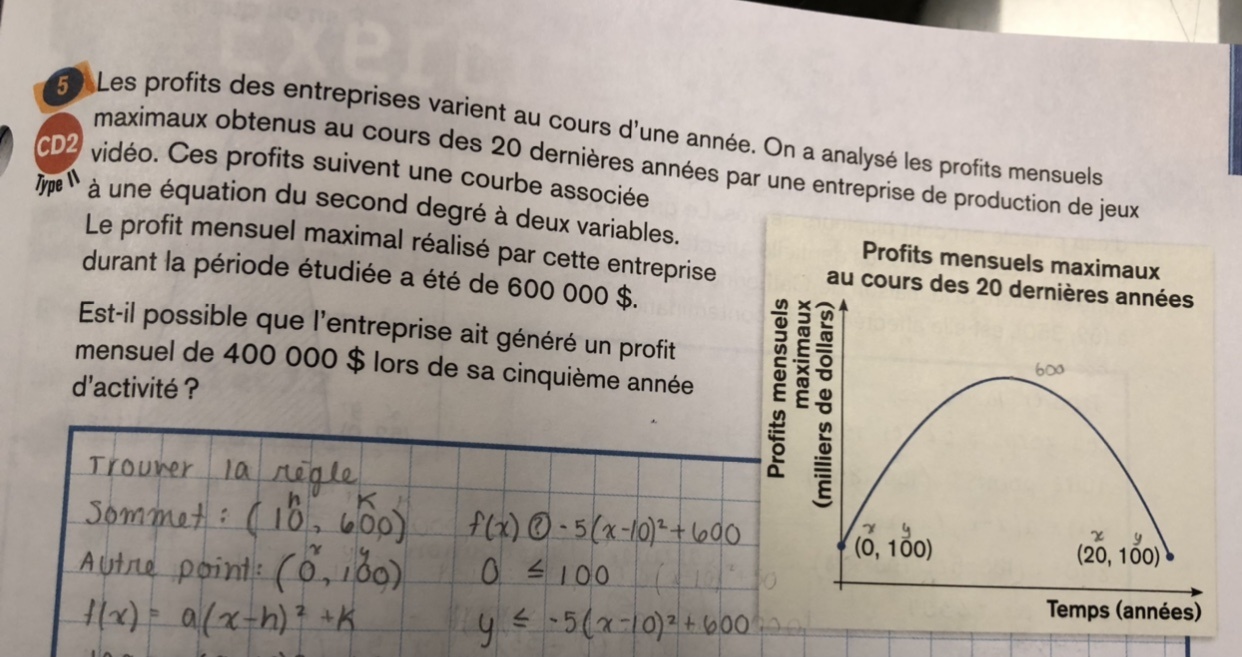
Pour le problème 5, j'arrive effectivement à la même règle que toi, bravo!
Tout ce qu'il reste à faire, c'est savoir s'il est possible que l'entreprise ait généré un profit mensuel de 400 00 $ lors de sa cinquième année. En d'autres mots, on cherche lorsque \(x = 5\) (le temps = 5 ans), est-il vrai que \(y = 400\) (profit = 400 000 $) ?
Pour y parvenir, il suffit de remplacer ces valeurs dans la règle trouvée. S'il y a bel et bien égalité des deux côtés, alors il est possible d'affirmer que cela a été possible! Si le résultat est plus grand que 400, on peut confirmer que le profit de 400 000 $ a même été dépassé ! Si le résultat est plus petit, on peut confirmer qu'il a été impossible que l'entreprise atteint les 400 000 $.
Je t'invites donc à trouver, selon ta règle \(f(x) = - 5 ( x - 10)^2 + 600\), si
\(400 = -5 (5-10)^2 + 600\) ?
Quant à la dernière question, le problème 8, un certain nombre y est supérieur à deux nombres impairs consécutifs.
Nous savons que n'importe quoi multiplié par 2 donne un nombre pair. Ainsi, un nombre pair peut s'écrire $$ a_n = 2n $$ où n est un nombre entier.
Pour le rendre impair, il ne suffit que d'ajouter un 1!
$$ a_{n+1} = 2n + 1 $$
Par exemple,
Pour \(n = 0\) : \(2n + 1 = 2(0) + 1 = 1\) impair!
Pour \(n = 1\) : \(2n + 1 = 2(1) + 1 = 3\) impair!
Pour \(n = 2\) : \(2n + 1 = 2(2) +1 = 5\) impair!
Et ainsi de suite …
Alors, le premier nombre est \(2n + 1\) et puisque les deux sont consécutifs, le deuxième est \(2n + 3\).
On observe qu'on n'ajoute pas seulement +1 à cause qu'ils sont consécutifs car on veut seulement les nombres impairs. Si nous ajoutions que 1 au premier nombre, nous nous retrouvions avec un nombre pair ... On veut consécutif, oui, mais qu'ils restent impairs et nous savons que d'un nombre impair à l'autre on fait un bond de 2!
De ce fait, \(y > (2n + 1) x (2n+3)\)
Si tu es plus à l'aise de travailler avec des x que des n, tu peux la transformer comme ceci:
$$ y > (2x + 1)(2x+3) $$
Et voilà la règle!
Bonne continuation!
Suggestions en lien avec la question
Suggestion en lien avec la question
Voici ce qui a été trouvé automatiquement sur le site, en espérant que ça t’aide!