Matières
Niveaux
Le rôle des paramètres dans une fonction polynomiale de degré 2
Fiche | Mathématiques
Cette fiche présente le rôle des différents paramètres d'une fonction polynomiale de degré 2 sous la forme canonique, sous la forme générale et sous la forme factorisée.
Secondaire
4-5
Table des matières
- Haut de page
- Manipulation animée des paramètres
- L'analyse du paramètre |a|
- Un changement d'échelle vertical de la courbe de facteur |a|
- Une réflexion du graphique de la fonction par rapport à l'axe des |x|
- L’effet des modifications d’un paramètre sous la forme canonique
- L'analyse du paramètre |h|
- L'analyse du paramètre |k|
- L’effet des modifications d’un paramètre sous la forme générale
- L'analyse du paramètre |b|
- L'analyse du paramètre |c|
- L'effet des modifications d'un paramètre sous la forme factorisée
- L'analyse des paramètres |{ x }_{ 1 }| et |{ x }_{ 2 }| (les zéros)
- Exercice
La forme de base d'une fonction polynomiale de degré 2 est |f(x)=x^{2}|
Lorsqu’on transforme cette forme de base, on obtient une équation avec différents paramètres.
La forme canonique : |f(x)=a(x−h)^2+k| où |h| et |k| sont les coordonnées du sommet.
La forme générale : |f(x)=ax^2+bx+c| où |c| est l'ordonnée à l'origine.
La forme factorisée : |f(x)=a(x−x_1)(x−x_2)| où |x_1| et |x_2| sont les zéros de la parabole.
Remarque : Le paramètre |a| est toujours le même, peu importe la forme d'écriture, et il doit être différent de zéro.
Manipulation animée des paramètres
Dans l'animation suivante, tu peux modifier les paramètres de la fonction polynomiale de degré 2. Observe bien les modifications qui s'opèrent sur la courbe transformée (en noir) par rapport à la fonction de base (en vert). Tu peux en profiter pour observer l'effet de la modification des paramètres sur les propriétés de la fonction. Par la suite, tu pourras poursuivre la lecture de la fiche pour avoir toutes les précisions sur chacun des paramètres de chacune des formes d'écriture de la fonction.
L'analyse du paramètre |a|
Un changement d'échelle vertical de la courbe de facteur |a|
Le paramètre |a| est responsable de l’ouverture (l'étirement vertical) de la parabole.
Lorsque |a| est plus grand que |1\ (a>1)| :
Plus le paramètre |a| est grand, plus l’ouverture de la parabole est petite, c'est-à-dire que les deux branches de la courbe se rapprochent de l'axe des |y.| La fonction subit donc un étirement vertical.
Lorsque |a| est entre |0| et |1\ (0<a<1)| :
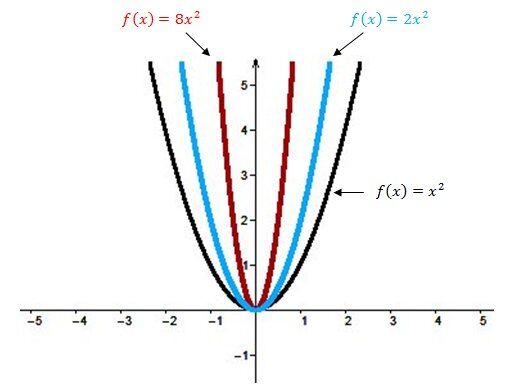
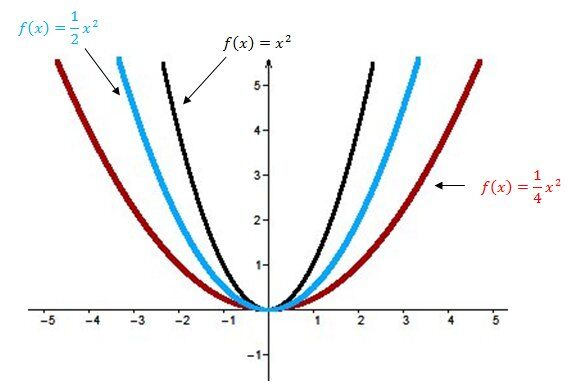
Plus le paramètre |a| est petit (près de 0), plus l’ouverture de la parabole est grande, c'est-à-dire que les deux branches de la courbe s'éloignent de l'axe des |y.| La fonction subit donc un rétrécissement vertical.
Une réflexion du graphique de la fonction par rapport à l'axe des |x|
Lorsque |a| est positif |(a>0)| :
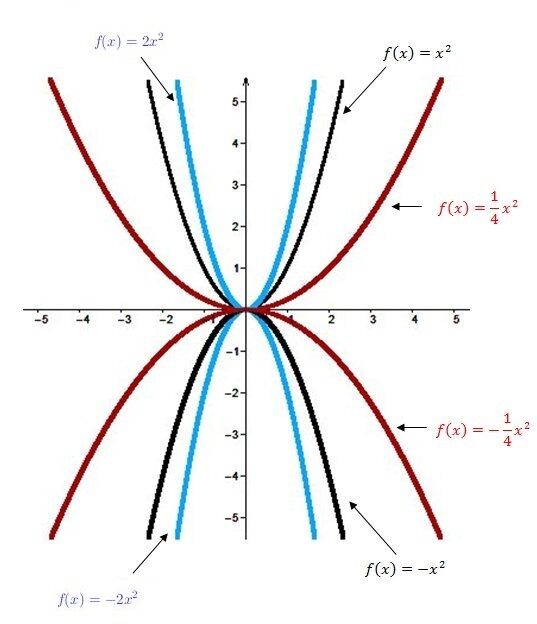
L'ouverture de la parabole est vers le haut.
Lorsque |a| est négatif |(a<0)| :
L'ouverture de la parabole est vers le bas.
L’effet des modifications d’un paramètre sous la forme canonique
La forme canonique : |f(x)=a(x−h)^2+k| où |a|, |h| et |k| sont les paramètres de la fonction.
Remarque : Le paramètre |a| doit être différent de zéro.
L'analyse du paramètre |h|
Lorsque |h| est positif |(h>0)| :
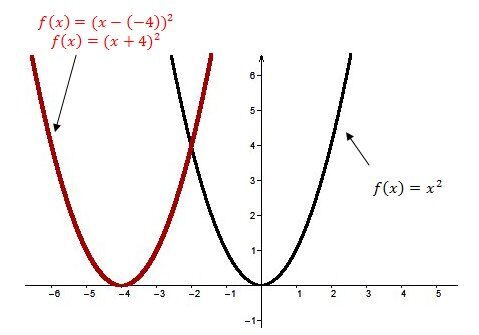
La courbe de la fonction polynomiale de degré 2 subit une translation vers la droite.
Lorsque |h| est négatif |(h<0)| :
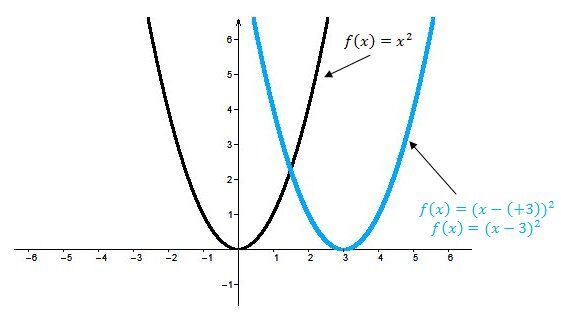
La courbe de la fonction polynomiale de degré 2 subit une translation vers la gauche.
L'analyse du paramètre |k|
Lorsque |k| est positif |(k>0)| :
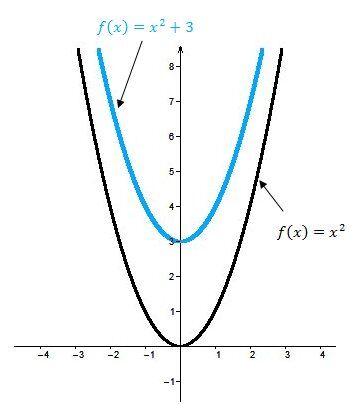
La courbe de la fonction polynomiale de degré 2 subit une translation vers le haut.
Lorsque |k| est négatif |(k<0)| :
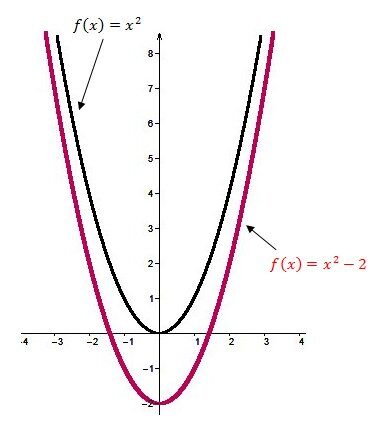
La courbe de la fonction polynomiale de degré 2 subit une translation vers le bas.
Dans la forme canonique, les paramètres |h| et |k| fournissent les coordonnées du sommet de la parabole dans le plan cartésien. ||\text{Sommet}=(h,k)||
L’effet des modifications d’un paramètre sous la forme générale
La forme générale : |f(x)=ax^2+bx+c| où |a|, |b| et |c| sont les paramètres de la fonction.
Remarque : Le paramètre |a| doit être différent de zéro.
Dans la forme générale, le paramètre |a| est le même que dans la forme canonique et que dans la forme factorisée. Il a donc les mêmes effets sur la parabole. Voici quelques exemples :
L'analyse du paramètre |b|
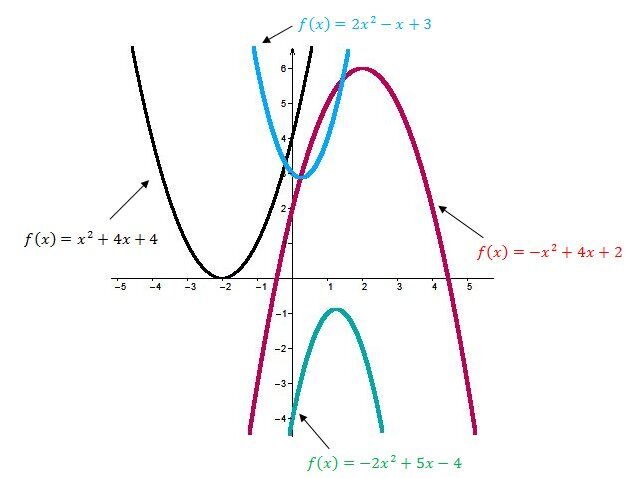
Lorsqu’on fait varier le paramètre |b| d’une fonction polynomiale de degré 2 sous sa forme générale, on peut alors observer une translation oblique du sommet (qui suit la forme d'une parabole). Attention, l'influence du paramètre |b| sur le graphique dépend d'abord du signe du paramètre |a| de la parabole. En effet, la direction du déplacement de la parabole sera différente selon que le paramètre |a| est positif ou négatif.
Lorsque |b| est positif |(b>0)| :
La parabole se déplace vers la gauche et vers le bas si |a>0|. Elle se déplace vers la droite et vers le haut si |a<0|.
Dans l'exemple suivant, les valeurs de |a| et |c| sont fixes |(a=1| et |c=0)| et la valeur de |b| varie.
Lorsque |b| est négatif |(b<0)| :
La parabole se déplace vers la droite et vers le bas si |a>0|. Elle se déplace vers la gauche et vers le haut si |a<0|.
Dans l'exemple suivant, les valeurs de |a| et |c| sont fixes |(a=1| et |c=0)| et la valeur de |b| varie.
L'analyse du paramètre |c|
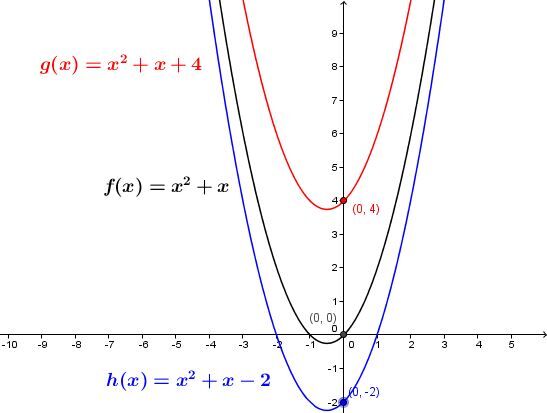
Dans la forme générale, le paramètre |c| nous donne la valeur de l’ordonnée à l’origine, c’est-à-dire la valeur de |y| lorsque |x=0.|
Concrètement, si on augmente la valeur du paramètre |c,| la courbe subit une translation vers le haut. Si on diminue la valeur de |c,| la courbe subit une translation vers le bas.
L'effet des modifications d'un paramètre sous la forme factorisée
La forme factorisée : |f(x)=a(x−{ x }_{ 1 })(x−{ x }_{ 2 })| où |a,| |{ x }_{ 1 }| et |{ x }_{ 2 }| sont les paramètres de la fonction.
Remarque : Le paramètre |a| doit être différent de zéro.
Dans la forme factorisée, le paramètre |a| est le même que dans la forme cannonique et que dans la forme générale. Il a donc les mêmes effets sur la parabole.
L'analyse des paramètres |{ x }_{ 1 }| et |{ x }_{ 2 }| (les zéros)
Dans la forme factorisée, les paramètres |{ x }_{ 1 }| et |{ x }_{ 2 }| donnent la valeur des zéros de la fonction, c’est-à-dire les valeurs de |x| lorsque |y=0.|
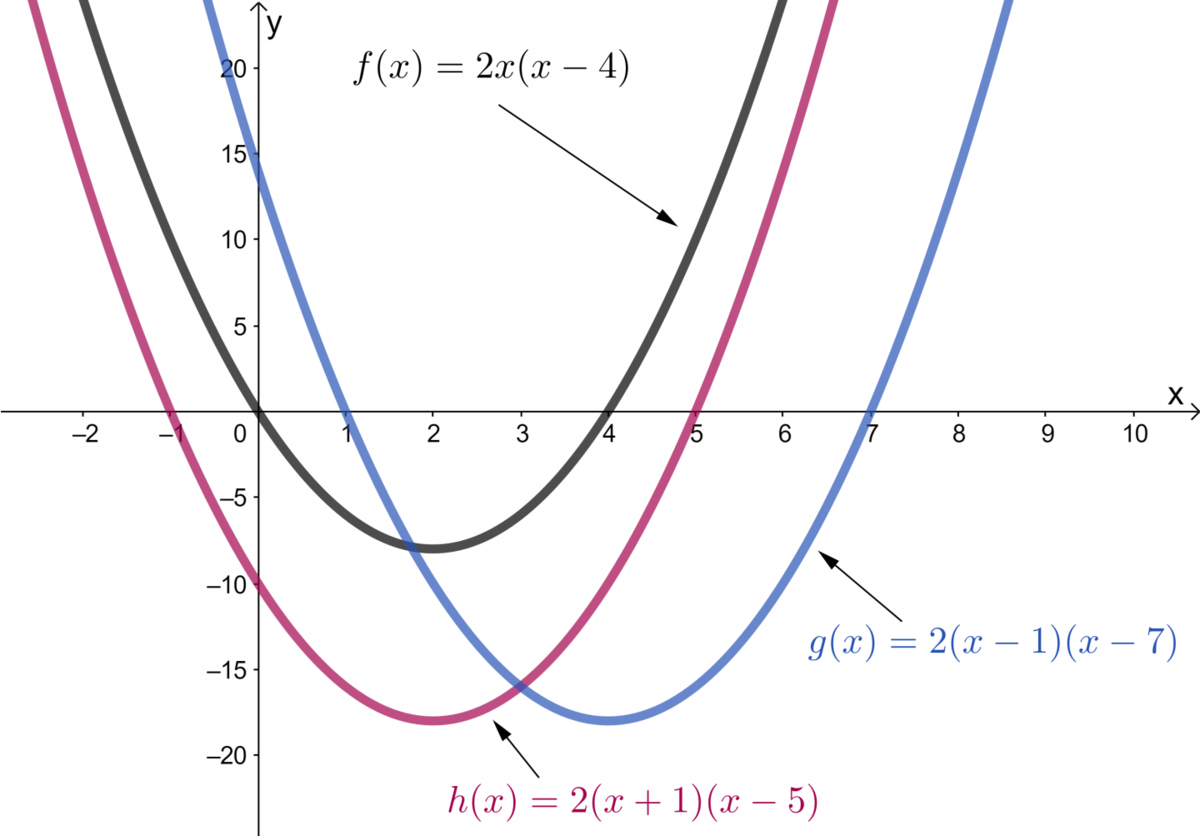
Une fonction polynomiale de degré 2 ne peut pas s'écrire sous la forme factorisée lorsque la courbe ne croise pas l'axe des |x,| c'est-à-dire lorsqu'il n'y a pas de zéros.