Secondaire 2 • 4a
Bonjour, je ne comprends pas comment trouver la hauteur du prisme 1.
Bonjour, je ne comprends pas comment trouver la hauteur du prisme 1.
Explication d'Alloprof
Cette explication a été donnée par un membre de l'équipe d'Alloprof.
Salut à toi, FourmiFantastique7921!
Merci de faire appel à nos services. :)
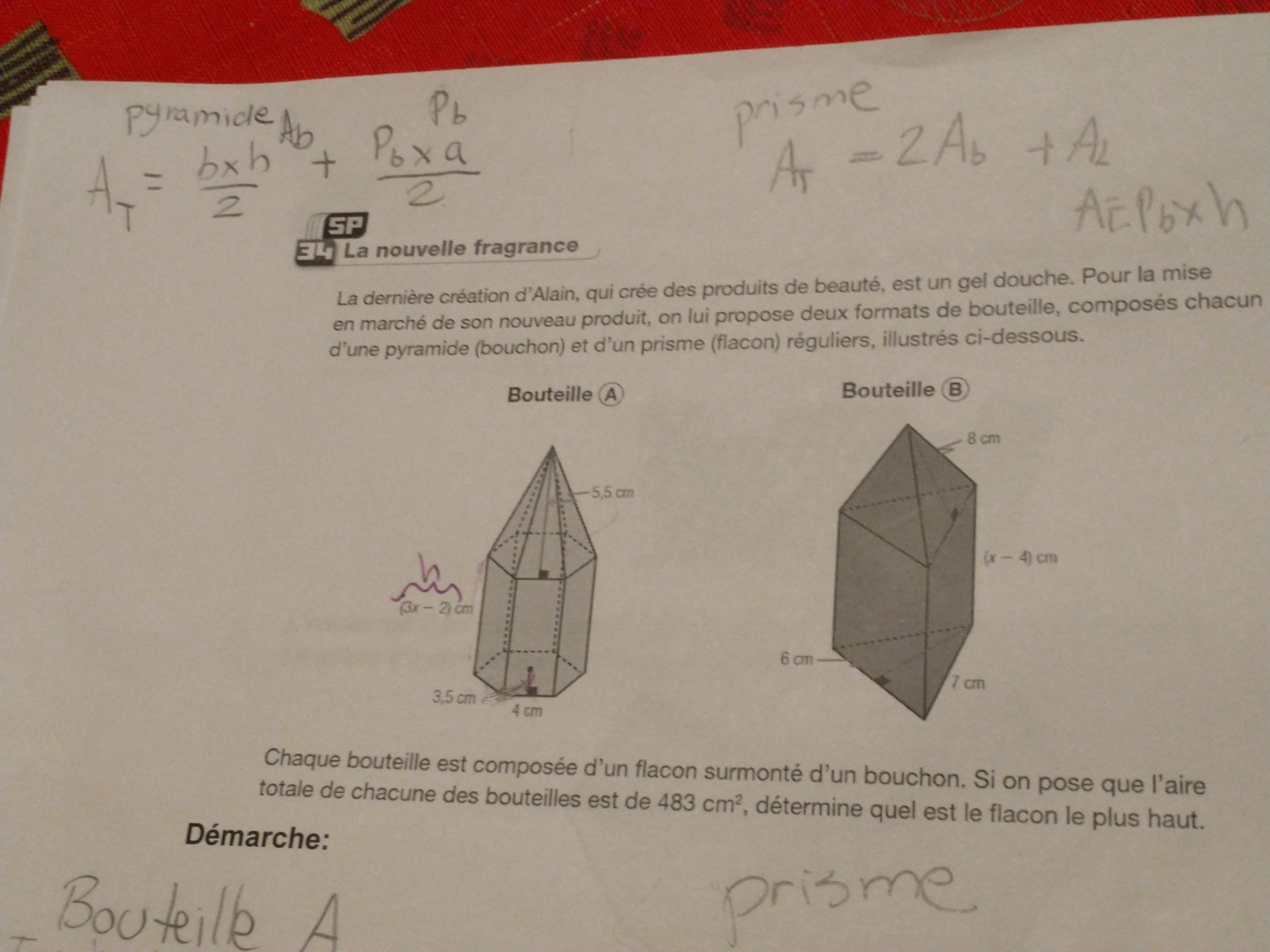
Quand tu te réfères au prisme 1, j'imagine que tu fais référence au prisme à base hexagonale de la bouteille A. Celui-ci est formé de deux hexagones (bases) et de six rectangles (faces latérales).
On te dit que la hauteur du prisme correspond à l'expression (3x - 2) cm. Pour trouver la valeur numérique de la hauteur du prisme, il faut donc trouver le x.
Pour faire cela, tu dois former une expression qui représente l'aire totale de la bouteille. Cette expression est composée de l'aire de la pyramide à base hexagonale (A base hexagonale + A latérale) additionnée à l'aire de l'hexagone qui supporte la bouteille ainsi que l'aire latérale du prisme. PS : la formule est le périmètre de la base de ce prisme multiplié par la hauteur, soit (3x-2).
Voici un lien abordant l'aire d'une pyramide avec un polygone régulier comme base:
Voici un lien abordant l'aire d'un prisme:
Ensuite, forme une égalité entre l'expression algébrique qui définit l'aire totale de la bouteille A et l'aire totale de la bouteille (483 cm^2). Utilise la formule quadratique (des zéros) pour trouver le x pour pouvoir par la suite remplacer le x dans (3x-2) et calculer le tout. Tu trouveras la valeur numérique de la hauteur!
Je te laisse prendre connaissance de tout cela et n'hésite pas à nous écrire de nouveau pour plus de précisions. :)
Suggestions en lien avec la question
Suggestion en lien avec la question
Voici ce qui a été trouvé automatiquement sur le site, en espérant que ça t’aide!