Secondaire 5 • 2a
A quoi sert de restreindre le domaine de definition de cette fonction ? et pourquoi si on le faisait pas se serait impossible de définir cette fonction réciproque ?
il s agit de trouver la réciproque de cette fonction.
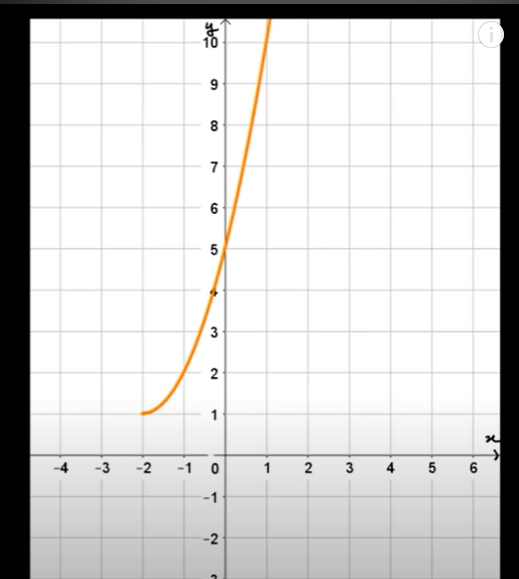
voici le graphique associee a la fonction , est ce que c est pour definir le domaine de la parabole, donc on veut pas le cote ou x est inferieur a -2 , est ce que cela aura un effet sur le graphique de la réciproque ou sinon c permet de choisir quelles branches parmis les 2 qui composent la reciproque de la parabole est a prendre ?merci
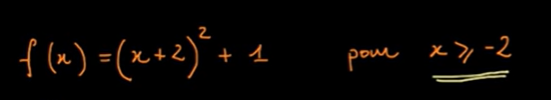






La fonction que tu as présenté est bien définie sur pour toute valeur de x dans R on peut calculer son image y=f(x) il n'y a pas de restriction proprement dite.
Par contre si on s'intéresse si la fonction a une fonction réciproque la réponse est non, examine le cas y=5 s'il n'y avait pas la restriction x>=-2 y=5 aurais eu deux antécédents x=0 et x=-4
paracerque f(0)=5 et f(-4)=5
de même y=10 aurais eu deux antécédents x=1 et x=-6
Dans ce cas le fonction étudiée n'as pas de fonction réciproque
On sait que la fonction réciproque quand elle existe; est la fonction qui a tout y de l'ensemble d'arrivé associe au plus un x de l'ensemble de départ et on la note f-1(x)
Par contre si on restreint le domaine de départ x>=-2 tout élément y aura un seul antécédent
Dans ce cas on peut parler de fonction réciproque de (x+2)²+1
par exemple voir graphe
y=1 a un seul antécédent c'est x=-2
y=2 a un seul antécédent c'est x=-1
y=5 a un seul antécédent c'est x=0
Trouver la fonction réciproque revient donc a résoudre l'équation
y=(x+2)²+1 c'est a dire tirer l'antécédent x en fonction de y
y-1=(x+2)² avec y>=1 on passe a la racine carrée
racine(y-1)=racine(x+2)² y>=1
racine(x+2)²=racine(y-1) y>=1
|x+2|=racine(y-1) y>=1
|x+2|=x+2 si x>=-2
|x+2|=-(x+2) si x<=-2
L'équation en x ---------- y=(x+2)²+1
a deux solutions
x+2=racine(y-1) si x>=-2 et y>=1
ou
-(x+2)=racine(y-1) si x<=-2 et y>=1
x=-2+racine(y-1) si x>=-2 et y>=1
ou
x=-2-racine(y-1) si x<=-2 et y>=1
pour un y>=1 si on maintient x dans tout R
tout y a deux antécédents vus précédemment,
par contre si on travail dans le domaine x>=-2
tout y>=1 a seulement un antécédent x=-2+racine(y-1)
dans ce cas la fonction f(x)=(x+2)²+1
de [-2, +linfini[ dans [1, +linfini[
a une fonction réciproque qu'on notera g
de [1, +linfini[ dans [-2, +linfini[ et qui a tout t appartenant a [1, +linfini[ associe
g(t)=-2+racine(t-1)
Explication d'Alloprof
Cette explication a été donnée par un membre de l'équipe d'Alloprof.
Salut !
La réciproque d'une fonction polynomiale du second degré n'est pas une fonction. Pour une valeur de y, il peut exister plus d'une valeur de x.
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Avec la restriction posée, il n'y a qu'une valeur de x pour chaque valeur de y. Si tu as d'autres questions, n'hésite pas !
Suggestions en lien avec la question
Suggestion en lien avec la question
Voici ce qui a été trouvé automatiquement sur le site, en espérant que ça t’aide!