Zone d’entraide

QuartzFormidable559

Bonsoir, Merci d'avoir répondu à ma question précédente, ça m'a vraiment beaucoup aidé 🤗. Pouvez-vous aussi m'aider pour les questions b et c svp ? Trouver les inconnus r et R me semble un peu compliqué

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

AvocatTenace6777

@

Équations :

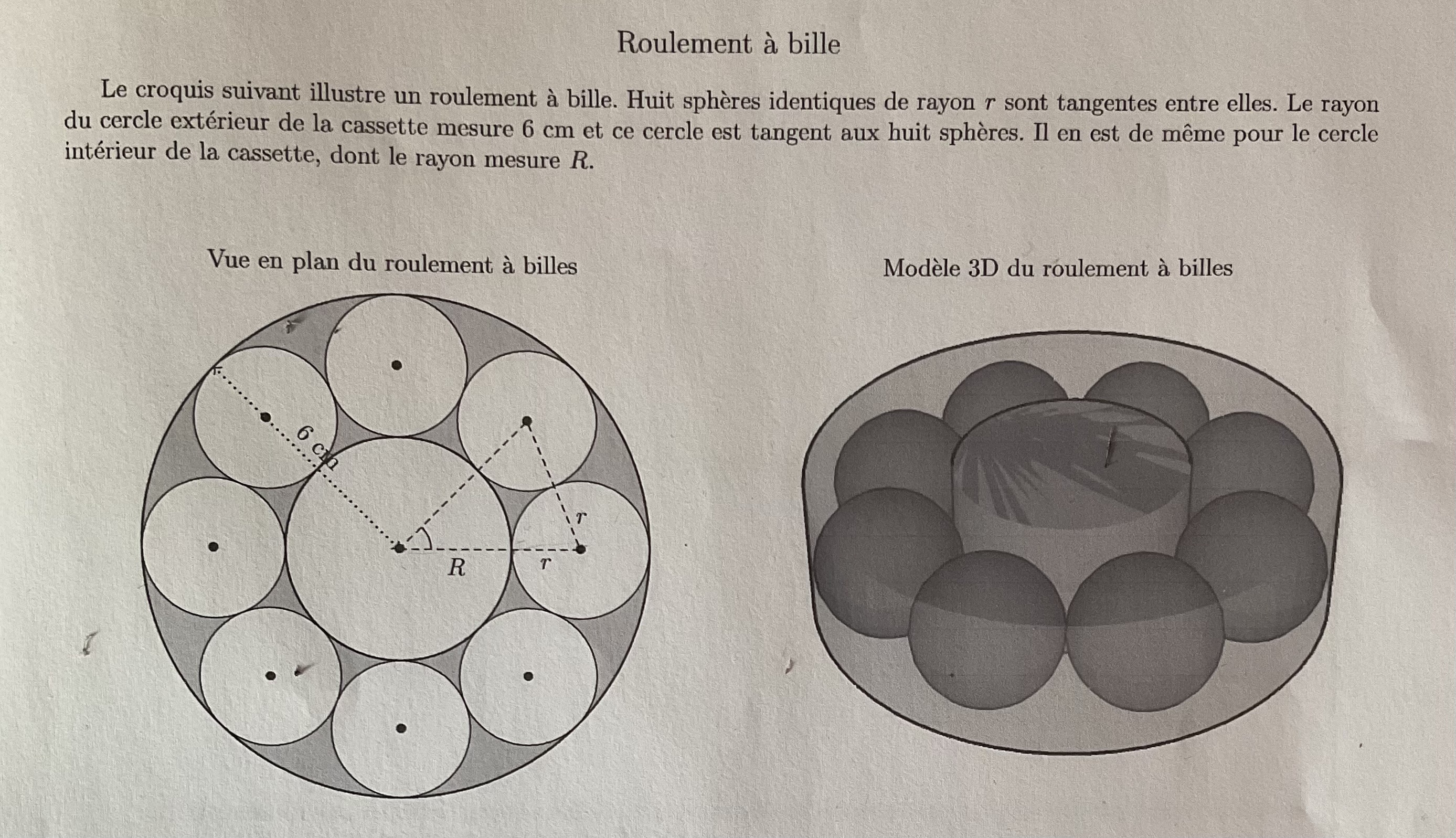
R+2r = 6

et par la loi des sinus dans le triangle isocèle en pointillés:

2r/sin45° = (R+r)/sin67,5°

.

Katia K

Re salut!

Contente que mon explication t'ait été utile! :D

Pour trouver la valeur des variables r et R, tu dois résoudre le système d'équations que nous avons trouvé précédemment, soit :

$$ R+2r=6$$

$$4r^2=(R+r)^2(2-\sqrt{2})$$

Pour ce faire, utilisons la méthode de substitution. Nous allons commencer par isoler R dans la première équation :

$$ R+2r=6$$

$$ R+2r-2r=6-2r$$

$$ R=6-2r$$

Puis, nous allons insérer l'expression correspondante à la variable R dans la seconde équation, comme ceci :

$$4r^2=(R+r)^2(2-\sqrt{2})$$

$$4r^2=((6-2r)+r)^2(2-\sqrt{2})$$

On simplifie l'équation :

$$4r^2=(6-2r+r)^2(2-\sqrt{2})$$

$$4r^2=(6-r)^2(2-\sqrt{2})$$

$$4r^2=(6-r)^2(0,5858)$$

Nous allons maintenant développer l'expression, plus particulièrement le (6-r)² :

$$4r^2=(6-r)(6-r)(0,5858)$$

$$4r^2=(36-6r-6r+r^2)(0,5858)$$

$$4r^2=(36-12r+r^2)(0,5858)$$

$$4r^2=(36-12r+r^2)(0,5858)$$

On distribue la multiplication sur chaque terme de la parenthèse :

$$4r^2=21,088-7,029r+0,5858r^2$$

On déplace le terme du côté gauche de l'équation :

$$4r^2-4r^2=21,088-7,029r+0,5858r^2-4r^2$$

$$0=21,088-7,029r+(0,5858-4)r^2$$

$$0=21,088-7,029r-3,414r^2$$

On peut réordonner nos termes pour que l'expression soit plus lisible :

$$0=-3,414r^2-7,029r+21,088$$

Tu peux ensuite utiliser la formule quadratique pour résoudre cette équation.

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

$$ x_{1,2} = \frac{-(-7,029) ± \sqrt{(-7,029)^2-4(-3,414)(21,088)}}{2(-3,414)} $$

Je te laisse faire le dernier calcul. Voici une fiche qui pourrait t'être utile : La résolution de systèmes d'équations linéaires | Secondaire | Alloprof

Si tu as d'autres questions, on est là! :)